matlab用最小欧氏距离,一种基于欧氏距离线性化逼近的设施选址最优化方法与流程...

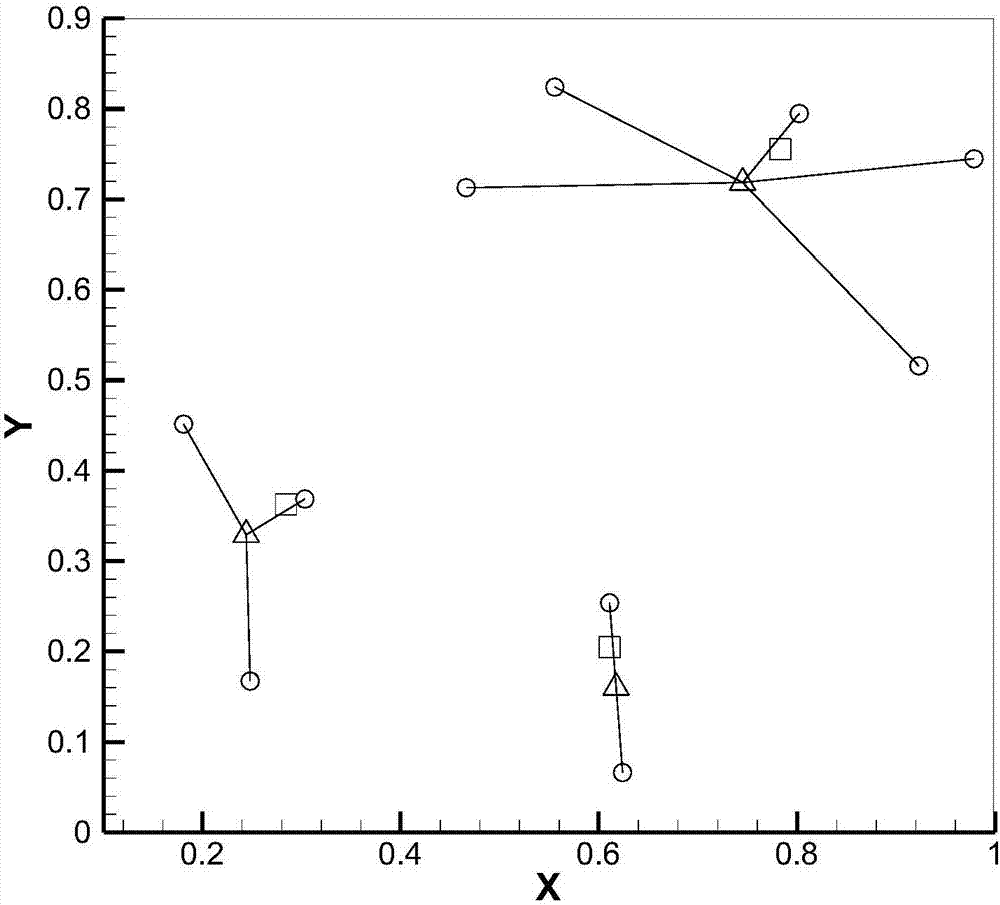
本发明提供一种基于将欧氏距离线性化的设施最优选址的方法，它可用于在城市公共设施规划，针对现有的城市居民的分布，求解最优的垃圾仓库点坐标选址以及相应的居民分配，以减少居民与其所分配的垃圾仓库之间的运输成本，属于物流设施规划与选址领域。

二、

背景技术：

在物流设施规划领域，仓库选址问题是影响运输成本和效率的关键问题。。在经济发展过程中，我们经常需要设置一个或多个集散物质、传输信息或执行某种服务的“仓库”点，以便为其周边的节点传输信息或者提供服务。例如，在城市建设和规划商业中心、医院、消防站、停车场、垃圾回收站点等公共设施时，经常需要考虑将中心点选在什么位置才能使城市系统运行效能最佳。因此，在实际问题中，这些选址问题也就是关于设施最优选址的问题。如何选择服务站点的地址，在保证每个客户点被分配给合适的站点服务的前提下，使得所有客户点到其对应的服务点的总距离最短，是物流选址领域的一个难题。

该设计问题目前均为利用传统k-均值(即k-means)计算，但该方法需要预先给定初始中心点，计算结果受到初始中心点选择的影响，并且该方法的均值法计算中心点不能保证是最优距离中心，所以不能计算出最优解。本发明提出一种基于欧氏距离线性化的最优选址方法，该方法是一种全局优化的方法，保证了计算结果可以控制在任意小的误差范围之内，且避免了初始解对最终结果的影响。

三、

技术实现要素：

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！