哈夫曼树及哈夫曼编码笔记
提示:文章还没写完,后续会更新。
文章目录
给定n个权值作为n个叶子结点,构造一棵二叉树,若该树的带权路径长度(wpl)达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树(HuffmanTree),还有的书翻译为霍夫曼树。
所以得出结论:所谓哈夫曼树就是wpl最小的二叉树,也称为最优二叉树;
重要概念:
- 路径和路径长度:在一棵树中,从一个结点往下可以达到的孩子或孙子结点之间的通路,称为路径。通路中分支的数目称为路径长度。若规定根结点的层数为1,则从根结点到第L层结点的路径长度为L-1。
- 结点的权及节点的带权路径长度:若将树中结点赋给一个有着某种含义的数值,则这个数值称为该结点的权。结点的带权路径长度为:从根结点到该结点之间的路径长度与该结点的权的乘积。
- 树的带权路径长度:树的带权路径长度规定为所有叶子结点的带权路径长度之和,记为WPL(weightedpathlength),权值越大的结点离根结点越近的二叉树才是最优二叉树。
- WPL最小的就是赫夫曼树。
构造方式示例
首先,对将要操作的数组进行定义:假设记数组个数为n,我们将这n个元素看成n个节点;
n个节点对应的权值为{w1,w2,...wn};让n个节点构成的集合,集合为T={T1,T2,...Tn};
其中,“n个节点”表示n个叶子节点,也表示根节点,这n个节点都没有左右子树(如下面第一幅图,每一个节点都是叶子结点也是根节点)。哈夫曼树的构造是针对带权的叶子节点进行的,下图的数字即表示节点的权值:
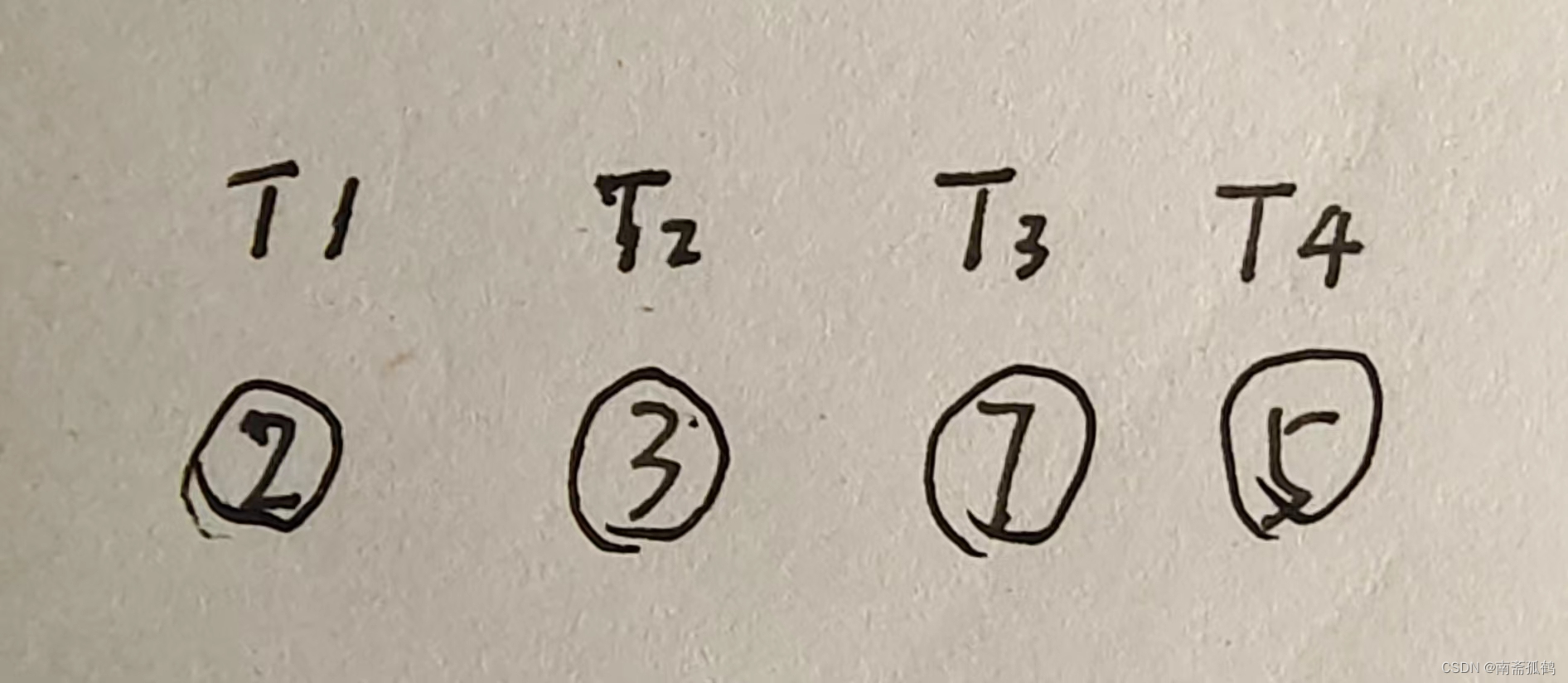
构造哈夫曼树的步骤
(1)选择与合并
从集合T中选择权值最小的两个节点,即2和3。使用权值最小的两个节点作为左右子树(图中的T1和T2),构造新的树T5,新的树的权值为左右子树权值之和:
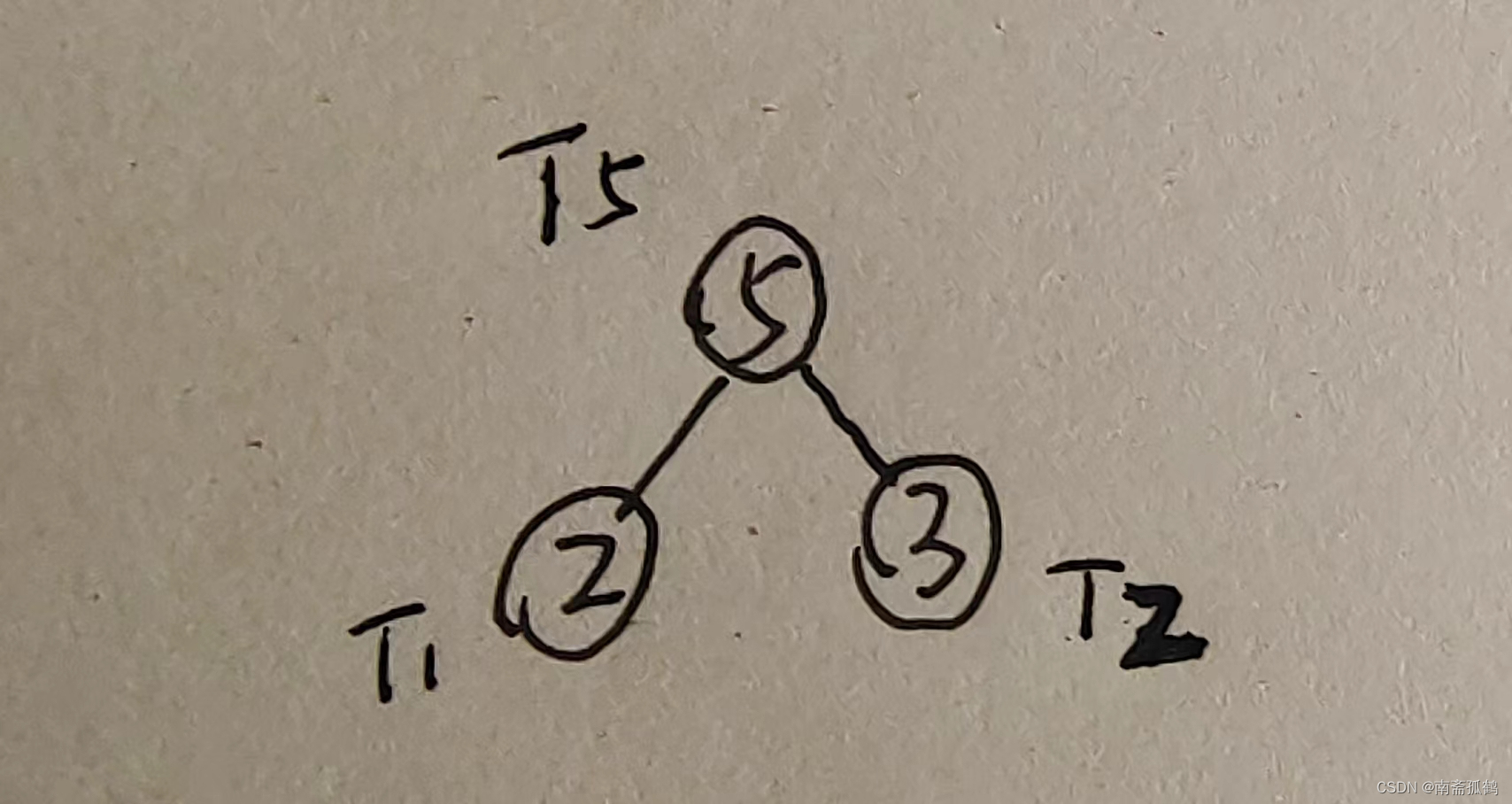
需要注意的是,使用权值最小的两个节点构建新的树时,应该将权值较小的节点T1作为左子树,权值较大的节点T2作为右子树。(如果T1和T2的权值相同,则将深度较小的作为左子树)比如在上图的基础上加入一个权值为5的节点——显然之前第一次的树的深度大于新节点,所以新树在左
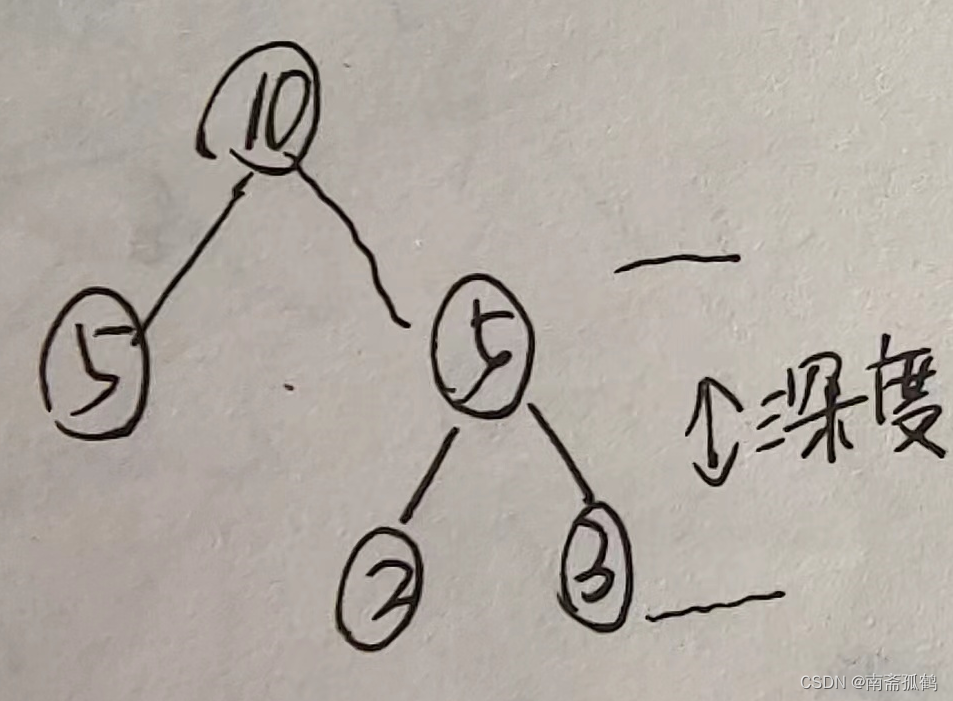
(2)增加与删除
从集合T中删除权值最小的两个节点(即T1和T2),然后将新创建的节点加入集合T(即T5)。此时,集合T={T3, T4, T5}。
经过一次合并以后,集合T的节点数目减一。减少两个节点,新增一个节点。
(3)重复操作
不断的重复上述两个步骤,直到集合T只剩下一个元素为止,即最后哈夫曼树的根节点。然后我们就可以对该节点进行遍历,就可以得到哈夫曼树;
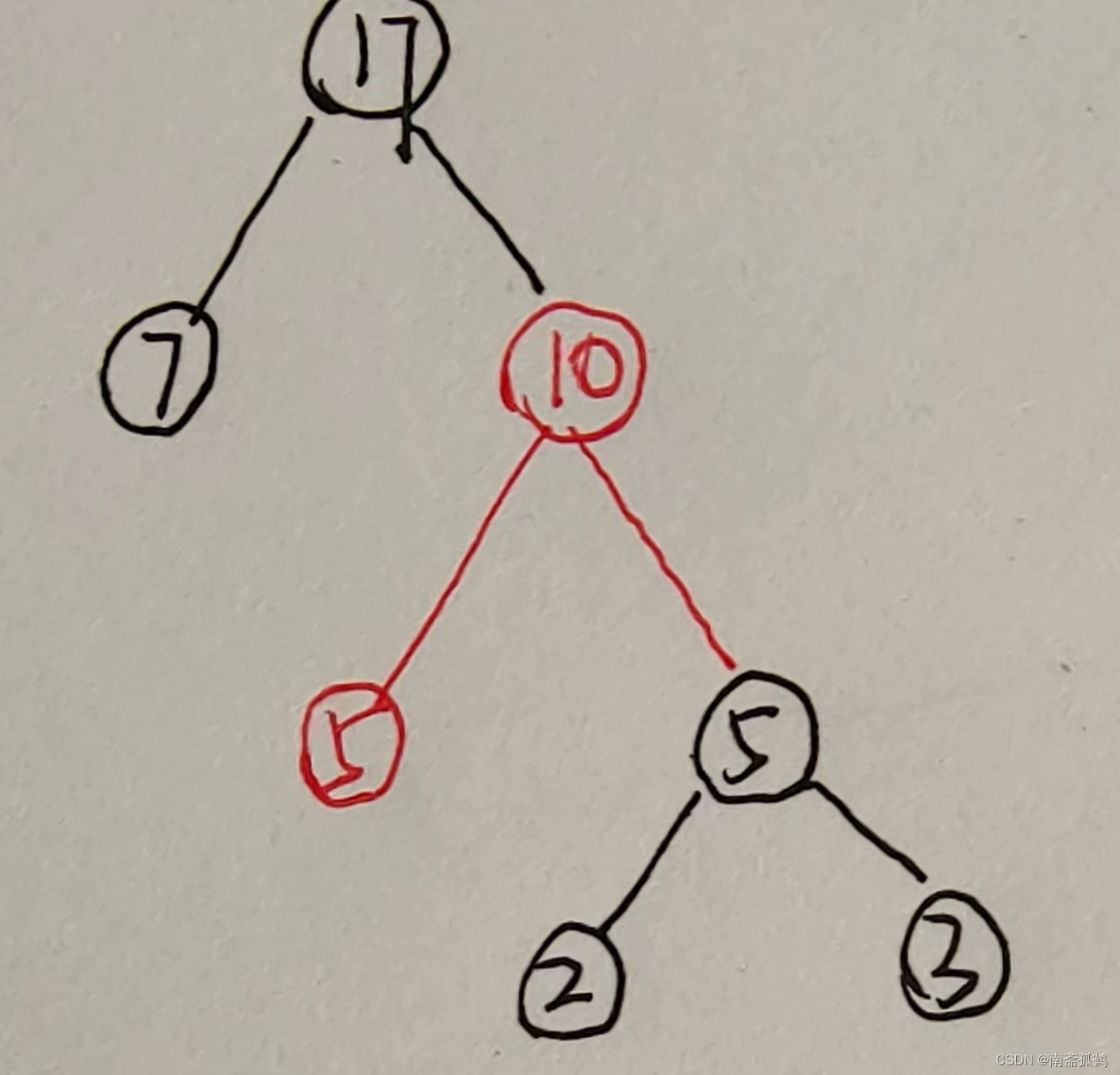
构建哈夫曼树时,各个步骤涉及到了几个非常重要的概念:
寻找集合T中权值最小的两个节点;并使用两个权值最小的节点构建新的节点;
在许多实际应用中,树中结点常常被赋予一个表示某种意义的数值,称为该结点的权。从树根结点到任意结点的路径长度(经过的边数)与该结点上权值的乘积,称为该结点的带权路径长度。树中所有结点的带权路径长度之和称为全树的带权路径长度,记为: WPL=∑i=1nWiLi , Wi 是第i个结点所带的权值,Li 是该结点到根结点的路径长度。
在含有n个带权叶子的二叉树中,其中带权路径长度(WPL)最小的二叉树称为哈夫曼树,也称最优二叉树。
哈夫曼树的构造算法描述如下:
- 将这n个结点分别作为n棵仅含有一个结点的二叉树,构成森林F。
- 构造一个新结点,从F中选取两颗树节点权值最小的树作为新结点的左、右子树,并且将新节点的权值置为左、右子树上根结点的权值之和。
- 从F中删除刚选出的两棵树,同时将新得到的树加入到F中。
- 重复步骤2和3,直至F中只剩下一棵树为止。
从上述构造过程中可以看出哈夫曼树具有如下特点:
- 每个初始结点最终都成为叶结点,且权值越小的节点到根结点的路径长度越大。
- 构造过程中共新建了 n-1 个结点,因此哈夫曼树中的结点总数为 2n - 1。
- 每次构造都选择 2 棵树作为新结点的孩子,因此哈夫曼树中不存在度为 1 的结点。
主要代码实现:
public static Node creatHuffmanTree(int arr[]){ List nodes = new ArrayList<>();for(int value:arr){nodes.add(new Node(value));}while(nodes.size() > 1){Collections.sort(nodes);System.out.println("从小到大排序后的权值为" + nodes);//取出根节点权值最小的两个节点Node leftNode = nodes.get(0);Node rightNode = nodes.get(1);//构建一个新的二叉树Node parent = new Node(leftNode.value + rightNode.value);parent.left = leftNode;parent.right = rightNode;//从ArrayList中删除处理过的二叉树节点nodes.remove(leftNode);nodes.remove(rightNode);//将parent加入到nodes中nodes.add(parent);}//返回哈夫曼树的root节点return nodes.get(0);}
}
哈弗曼编码:
赫夫曼编码也翻译为 哈夫曼编码(Huffman Coding),又称霍夫曼编码,是一种编码方式, 属于一种程序算法,赫夫曼编码是赫哈夫曼树在电讯通信中的经典的应用之一,广泛地用于数据文件压缩。其压缩率通常在 20%~90%之间;
赫夫曼码是可变字长编码(VLC)的一种。Huffman 于 1952 年提出一种编码方法,称之为最佳编码
原理剖析:通信领域中信息的处理方式 1-定长编码(ASCLL编码)
现给出我们一数据:i like like like java do you like a java,我们想这段数据用哈夫曼编码进行压缩。首先我们之前学过ASCLL码值,每个符号都有对应的值,我们先用它来进行压缩,如下图:

最终我们得到的信息总长度为359(包含空格),下面我么采用另一种方式;
通信领域中信息的处理方式 2-哈夫曼编码:(此编码满足前缀编码, 即字符的编码都不能是其他字符编码的前缀。不会造成匹配的多义性赫夫曼编码是无损处理方案)
首先我们对传输的 字符串( i like like like java do you like a java)进行各个字符出现的次数统计;得到结果—— d:1 y:1 u:1 j:2 v:2 o:2 l:4 k:4 e:4 i:5 a:5 :9(空格)
按照上面字符出现的次数构建一颗赫夫曼树, 次数作为权值
最终得到构建好的哈夫曼树,根据赫夫曼树,给各个字符,规定编码 (前缀编码), 向左的路径为 0 向右的路径为 1 , 结果如下::构成赫夫曼树的步骤:
- 从小到大进行排序, 将每一个数据,每个数据都是一个节点 , 每个节点可以看成是一颗最简单的二叉树
- 取出根节点权值最小的两颗二叉树
- 组成一颗新的二叉树, 该新的二叉树的根节点的权值是前面两颗二叉树根节点权值的和
- 再将这颗新的二叉树,以根节点的权值大小 再次排序, 不断重复 1-2-3-4 的步骤,直到数列中,所有的数据都被处理, 就得到一颗赫夫曼树
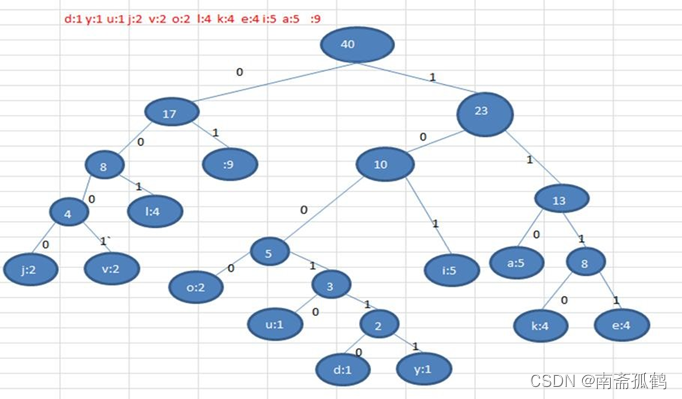
那么我们通过对每条路径进行遍历,我们可以得到如下编码:
| o: 1000 | u: 10010 | y: 100111 | d: 100110 |
| i: 101 | k: 1110 | e: 1111 | j: 0000 |
| a : 110 | v: 0001 | l: 001 | 空格:01 |
按照上面的赫夫曼编码,我们的"i like like like java do you like a java" 字符串对应的编码为 (注意这里我们使用的是无损压缩)
10101001101111011110100110111101111010011011110111101000011000011100110011110000110 01111000100100100110111101111011100100001100001110
在通过赫夫曼编码处理后的长度为133
说明:我们之前得到的长度是 359 , 压缩了 (359-133) / 359 = 62.9%,所以可以看出哈夫曼编码很可以利用更小的资源做更多的事,这就是他的优点;
注意事项
注意, 这个赫夫曼树根据排序方法不同,也可能不太一样,这样对应的赫夫曼编码也不完全一样,但是 wpl 是一样的,都是最小的, 最后生成的赫夫曼编码的长度是一样,比如: 如果我们让每次生成的新的二叉树总是排在权值相同的二叉树的最后一个,则生成的二叉树为:
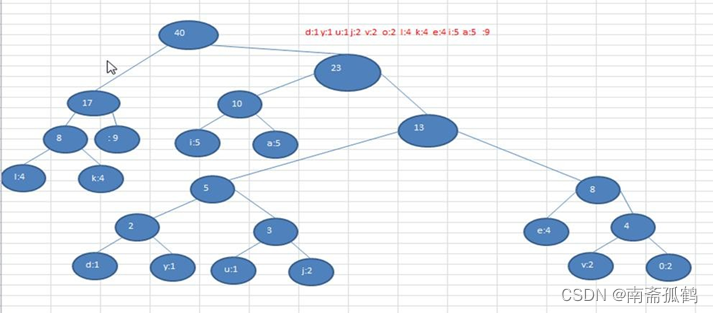
总结:
笔记来源是哔哩哔哩上韩顺平老师的课程之后摘抄的,仅便于自己复习;
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!