从公式说起

（1）条件概率
若事件 A 满足P(A)>0，对任意事件 B ，称
P ( B ∣ A ) = P ( A B ) P ( A ) P\left( B|A \right) =\frac{P\left( AB \right)}{P\left( A \right)} P(B∣A)=P(A)P(AB)​

其含义为在 A 发生的条件下，B 发生的概率

例子：

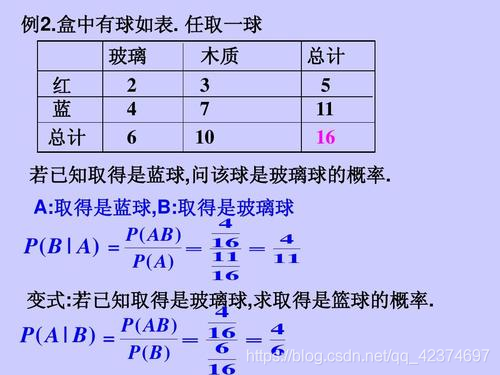
（2）全概率公式：
设 A 1 , A 2 , ⋯ , A n A_1,A_2,\cdots ,A_n A1​,A2​,⋯,An​ （n 为有限或者无穷），是样本空间 $\Omega$ 中的一个完备事件群（或为 $\Omega$ 的一个分划），满足 A i ∩ A j = ⊘ A_i\cap A_j=\oslash Ai​∩Aj​=⊘ 且 ∑ i = 1 n A i = Ω \sum_{i=1}^n{A_i}=\varOmega ∑i=1n​Ai​=Ω，设 B 为 $\Omega$ 中的一个事件，则全概率公式为：

∣ P ( B ) = ∑ i = 1 n P ( B ∣ A i ) P ( A i ) = P ( B ∣ A 1 ) P ( A 1 ) + P ( B ∣ A 2 ) P ( A 2 ) + ⋯ + P ( B ∣ A n ) P ( A n ) \left| \begin{array}{l} P\left( B \right) =\sum_{i=1}^n{P\left( B|A_i \right) P\left( A_i \right)}\\ \\ =P\left( B|A_1 \right) P\left( A_1 \right) +P\left( B|A_2 \right) P\left( A_2 \right) +\cdots +P\left( B|A_n \right) P\left( A_n \right)\\ \end{array} \right. ∣∣∣∣∣∣​P(B)=∑i=1n​P(B∣Ai​)P(Ai​)=P(B∣A1​)P(A1​)+P(B∣A2​)P(A2​)+⋯+P(B∣An​)P(An​)​

这个公式将整个事件 B 分解成一些两两互不相交的事件之和，也就是说，如果直接计算 $P(B)$ 不容易的话，可以将事件进行分解计算

可以把 全概率公式看作由 “原因”推“结果”，即如果把事件B看作结果，把诸事件 A 1 , A 2 . . . A n A_1,A_2...A_n A1​,A2​...An​ 看作导致这一结果的可能“原因”，则可以形象地把全概率公式看成由“原因”推“结果”。

（已知各个原因概率，推结果发生的概率）

例子：

（3）贝叶斯公式：

常见的

P ( A ∣ B ) = P ( B ∣ A ) P ( A ) P ( B ) P\left( A|B \right) =\frac{P\left( B|A \right) P\left( A \right)}{P\left( B \right)} P(A∣B)=P(B)P(B∣A)P(A)​

更具体地

若 A 1 , A 2 , ⋯ , A n A_1,A_2,\cdots ,A_n A1​,A2​,⋯,An​ 是 $\Omega$ 的一个划分，且 P ( A i ) > 0 ， i = 1 , 2 , ⋯ , n P\left( A_i \right) >0\text{，}i=1,2,\cdots ,n P(Ai​)>0，i=1,2,⋯,n，则对于任何概率不为零的事件 B ，有

P ( A i ∣ B ) = P ( A i ) P ( B ∣ A i ) P ( B ) = P ( A i ) P ( B ∣ A i ) ∑ j P ( A j ) P ( B ∣ A j ) ， i = 1 , 2 , ⋯ , n P\left( A_i|B \right) =\frac{P\left( A_i \right) P\left( B|A_i \right)}{P\left( B \right)}=\frac{P\left( A_i \right) P\left( B|A_i \right)}{\sum_j{P\left( A_j \right) P\left( B|A_j \right)}}\,\,\text{，}i=1,2,\cdots ,n P(Ai​∣B)=P(B)P(Ai​)P(B∣Ai​)​=∑j​P(Aj​)P(B∣Aj​)P(Ai​)P(B∣Ai​)​，i=1,2,⋯,n

把贝叶斯公式看作由“结果”推“原因”，现在有了结果 B ，在导致 B 发生的众多原因中，到底哪个原因导致了 B 发生（或者到底哪个原因导致 B 发生的可能性最大？）

例子：

三种信息

统计学有两个主要学派，频率学派与贝叶斯学派。

频率学派的观点：统计推断是根据样本信息对总体分布或总体的特征数进行推断，即用到两种信息（①总体信息、②样本信息）

贝叶斯学派的观点：除了上述两种信息以外，统计推断还应该使用第三种信息：③先验信息。贝叶斯统计就是利用先验信息、总体信息和样本信息进行相应的统计推断。

也就是说

贝叶斯统计学是基于总体信息、样本信息、先验信息这三种信息进行统计推断的方法和理论

这里，贝叶斯统计学与传统的经典统计学的主要区别就是。是否利用了先验信息以及是否将参数 θ 看成随机变量。

贝叶斯学派重视先验信息的收集、挖掘和加工，使之形成先验分布而参与到统计推断中，以提高统计推断的效果。如果忽略掉先验信息，将是一种信息损失。

总体信息：总体分布或所属分布族提供给我们的信息，例如：”总体是正态分布“

样本信息：从总体抽取的样本提供给我们的信息，样本越多，提供的信息越多，通过对样本的加工、整理，对总体的分布对总体的某些数字特征（均值、方差…）作出统计推断。

先验信息：人们在试验之前对要做的问题在经验上和资料上总是有所了解的，这些信息对统计推断是有益的。先验信息即是抽样（试验）之前有关统计问题的一些信息。一般说来，先验信息来源于经验和历史资料。先验信息在日常生活和工作中是很重要的。

先验概率（prior probability）：就是指根据以往经验和分析得到的概率，如全概率公式，它往往作为"由因求果"问题中的"因"出现的概率。

引用：先验概率和后验概率

事情还没有发生，根据以往的经验来判断事情发生的概率。是“由因求果”的体现。


扔一个硬币，在扔之前就知道正面向上的概率为0.5。这是根据我们之前的经验得到的。这个0.5就是先验概率。

先验概率的分类：

• 客观先验概率：利用过去历史资料计算得到的先验概率
• 主观先验概率：当历史资料无从取得或资料不完全时，凭人们的主观经验来判断而得到的先验概率

先验分布：就是在抽取样本 X 之前，对参数 $\theta$ 可能取值的认知，即对先验信息进行加工获得的分布称为先验分布。

对未知参数 $\theta$ 的先验信息用一个分布形式 $\pi \left(\theta \right)$ 来表示，此分布 $\pi \left(\theta \right)$称为未知参数 $\theta$ 的先验分布。

贝叶斯学派基本观点：对于任意未知量 $\theta$ 都可看作随机变量，可用一个概率分布去描述，这个分布就是先验分布 $\pi \left(\theta \right)$ ，在获得样本之后，总体分布、样本分布、先验分布通过贝叶斯公式结合起来，得到一个关于未知量 $\theta$ 的新分布——后验分布。之后关于 $\theta$ 的统计推断都可以基于 $\theta$ 的后验分布进行。

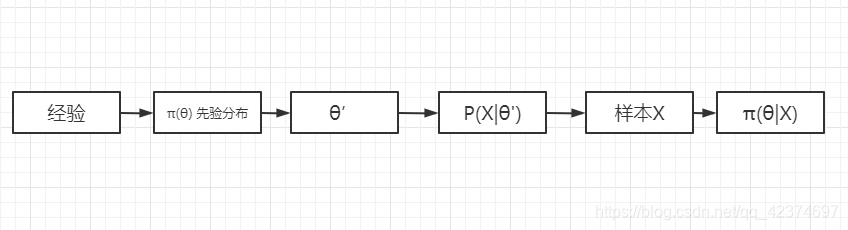后验分布集中了总体、样本和先验中有关 的一切信息,而又是排除一切与 $\theta$ 无关的信息之后得到的结果。

后验概率：基于新的信息，修正原来的先验概率后所获得的更接近实际情况的概率估计。先验概率和后验概率是相对的。如果以后还有新的信息引入，更新了现在所谓的后验概率，得到了新的概率值，那么这个新的概率值被称为后验概率。

这个概念有一点不好理解

我的理解是，比如说我们在正式的产品市场调查前，对公司产品合格率有一定了解，即根据以往的经验或资料可以得出公司生产的产品合格率的先验分布，由这个分布可以得出先验概率为$\pi \left(\theta \right)=0.8$（以往经验），随后通过调查或其它方式（抽取样本）获取了关于产品合格率的新信息，利用贝吐斯公式对先验概率$\pi \left(\theta \right)$进行修正，而后得到新概率，即后验概率 $\pi \left(\theta |x\right)=0.85$。

这里关于贝叶斯公式，有如下：

对于 $\theta$ 是连续型随机变量时，获得样本 X 后， $\theta$ 的后验分布就是在给定 X=x 条件下 $\theta$ 的条件分布，记为 $\pi \left(\theta |x\right)$ ,贝叶斯公式为

π ( θ ∣ x ) = h ( x , θ ) m ( x ) = f ( x ∣ θ ) π ( θ ) ∫ Θ f ( x ∣ θ ) π ( θ ) d θ \pi \left( \theta |x \right) =\frac{h\left( x,\theta \right)}{m\left( x \right)}=\frac{f\left( x|\theta \right) \pi \left( \theta \right)}{\int_{\varTheta}{f\left( x|\theta \right) \pi \left( \theta \right) d\theta}} π(θ∣x)=m(x)h(x,θ)​=∫Θ​f(x∣θ)π(θ)dθf(x∣θ)π(θ)​
其中 ， $\pi \left(\theta \right)$ 表示随机变量 $\theta$ 的概率函数

• 当 $\theta$ 为离散型随机变量时， π ( θ i ) \pi \left( \theta _i \right) π(θi​) 表示事件 { θ = θ i } \left\{ \theta =\theta _i \right\} {θ=θi​} 的概率分布，即概率 P ( θ = θ i ) P\left( \theta =\theta _i \right) P(θ=θi​)
• 当 $\theta$ 为离散型随机变量时， $\pi \left(\theta \right)$ 表示 $\theta$ 的密度函数

$\theta$ 的分布函数用 F π ( θ ) F^{\pi}\left( \theta \right) Fπ(θ) 表示

对于 $\theta$ 是离散型随机变量时，贝叶斯公式为

P ( θ = θ i X = ∣ x ) = P ( X = x ∣ θ = θ i ) P ( θ = θ i ) ∑ j P ( X = x ∣ θ = θ j ) P ( θ = θ j ) P\left( \theta =\theta _iX=|x \right) =\frac{P\left( X=x|\theta =\theta _i \right) P\left( \theta =\theta _i \right)}{\sum_j{P\left( X=x|\theta =\theta _j \right) P\left( \theta =\theta _j \right)}} P(θ=θi​X=∣x)=∑j​P(X=x∣θ=θj​)P(θ=θj​)P(X=x∣θ=θi​)P(θ=θi​)​

这个后验概率是通过抽取样本（考虑总体信息、样本信息、先验信息）对先验概率修正后的结果

一般说来，

• 先验分布 $\pi \left(\theta \right)$ 是反映人们抽样前对的 $\theta$ 的认识
• 后验分布 $\pi \left(\theta |x\right)$ 是反映人们在抽样后对 $\theta$ 的认识

它们之间的差异是由于样本 $x$ 出现后人们对 $\theta$ 认识的一种调整。

所以后验分布 $\pi \left(\theta |x\right)$ 可以看做是人们用总体信息和样本信息（综合称为抽样信息）对 $\pi \left(\theta \right)$ 作调整的结果。

案例

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！