SVM(Support Vector Machine)

Large Margin Classifier

Optimization Objective
SVM被广泛运用在工业和学术界之中，是在少量数据上训练的很好的模型.
Logistic Regression中的log(y’)和log(1-y’)被替换成了cost1($\theta$’*X)和cost2($\theta$’*X).
我们的Cost Function变成了: min ⁡ θ C ∑ i = 1 m [ y ( i ) cost ⁡ 1 ( θ T x ( i ) ) + ( 1 − y ( i ) ) cost ⁡ 0 ( θ T x ( i ) ) ] + 1 2 ∑ i = 1 n θ j 2 \min _{\theta} C \sum_{i=1}^{m}\left[y^{(i)} \operatorname{cost}_{1}\left(\theta^{T} x^{(i)}\right)+\left(1-y^{(i)}\right) \operatorname{cost}_{0}\left(\theta^{T} x^{(i)}\right)\right]+\frac{1}{2} \sum_{i=1}^{n} \theta_{j}^{2} minθ​C∑i=1m​[y(i)cost1​(θTx(i))+(1−y(i))cost0​(θTx(i))]+21​∑i=1n​θj2​
可以发现，当C足够大时，左边项会变为零，只留下右边 1 2 ∑ i = 1 n θ j 2 \frac{1}{2} \sum_{i=1}^{n} \theta_{j}^{2} 21​∑i=1n​θj2​,实际上可以写成 1 2 ∥ θ ∥ 2 \frac{1}{2}\|\theta\|^{2} 21​∥θ∥2,变成使它的范数最小. Optimization可以用约束二次最优规划.

Large Margin Intuition
SVM会将数据集用一条距离两边很远的直线分开. 并且在存在outlier且C很大的情况下，它会牺牲正确性，换来边际.

Mathematics behind Large Margin Classification

p(i)为x(i)在$\theta$上的投影的长度, p(i)*$\Vert \theta \Vert$为x(i)与$\theta$的点乘. 可以看出$\theta$是垂直于边界的，所以在想让自己的范数最小又正常分类的情况下，它会选择p(i)大的情况，因此边际就会变大.

Kernels

对于非线性情况，我们可以将数据映射到高维空间，然后用超平面去分开它们.

Andrew Ng介绍了一个核函数:
Gaussian Kernel

可以将f类比于polynomial regression里的单项式，只不过多项式回归的计算昂贵，我们发明了F. 上图的l(i)是landmarks, 对于一个变量x，我们有一组features F, f0为1
fi是衡量x与l(i)的相似度的，离得远就为0，离得近就为1.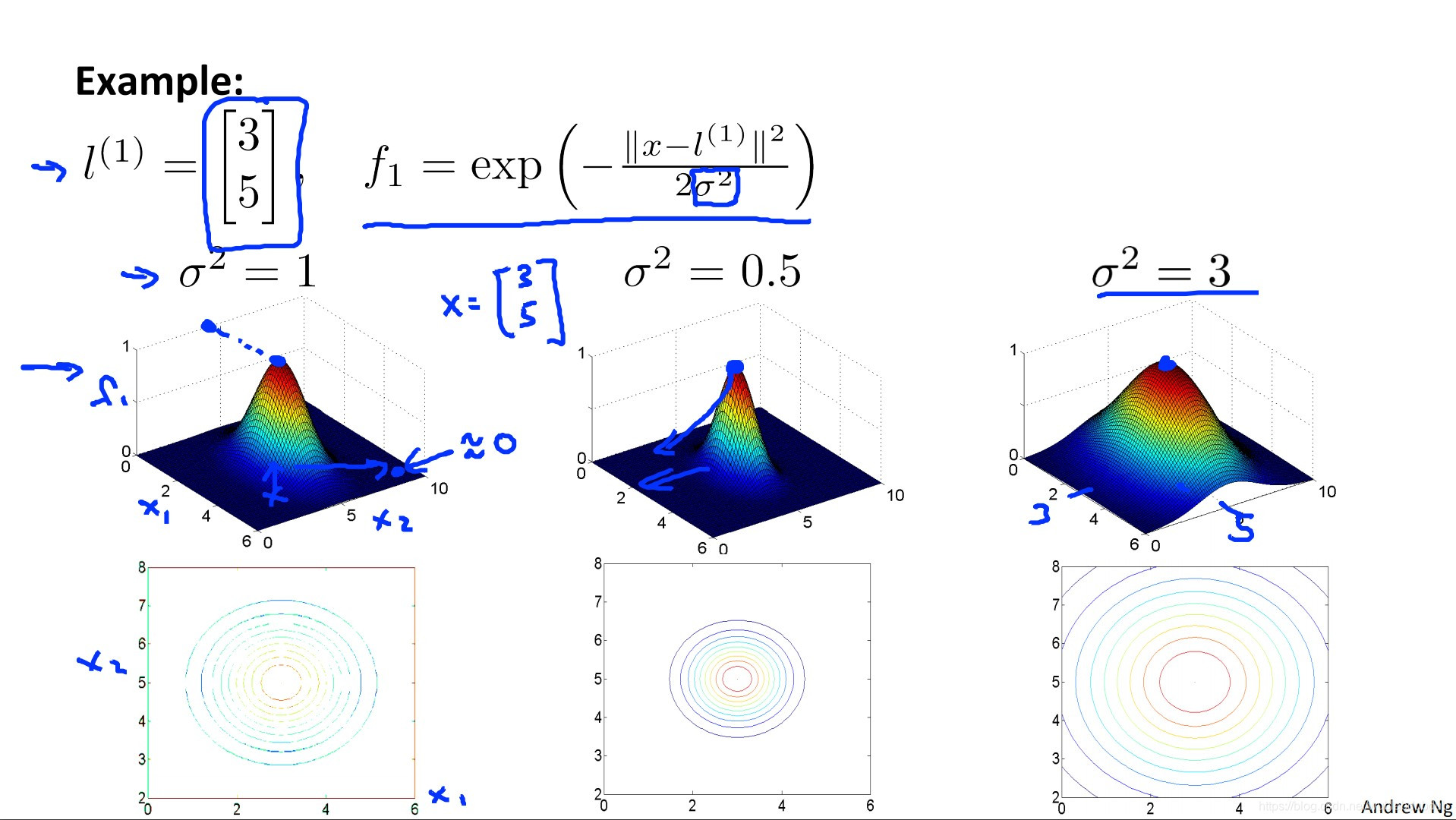
SVM + Kernel
min ⁡ θ C ∑ i = 1 m [ y ( i ) cost ⁡ 1 ( θ T f ( i ) ) + ( 1 − y ( i ) ) cost ⁡ 0 ( θ T f ( i ) ) ] + 1 2 ∑ i = 1 n θ j 2 \min _{\theta} C \sum_{i=1}^{m}\left[y^{(i)} \operatorname{cost}_{1}\left(\theta^{T} f^{(i)}\right)+\left(1-y^{(i)}\right) \operatorname{cost}_{0}\left(\theta^{T} f^{(i)}\right)\right]+\frac{1}{2} \sum_{i=1}^{n} \theta_{j}^{2} minθ​C∑i=1m​[y(i)cost1​(θTf(i))+(1−y(i))cost0​(θTf(i))]+21​∑i=1n​θj2​
对于SVM的参数在模型上的影响我们有：

SVM in Practive

总结:

1. 用内置函数，不要自己写
2. 看图
   

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！