1.马尔可夫决策过程MDP

1.1 MDP五元组

$MDP=<\mathcal{S},\mathcal{A},\mathcal{P},\mathcal{R},\gamma >$，其中：

• $\mathcal{S}$：状态空间
• $\mathcal{A}$：动作空间
• $\mathcal{P}$： P ( s ′ ∣ s , a ) \mathcal{P(s'|s,a)} P(s′∣s,a)为状态转移函数，表示采取动作$a$从状态$s$转移到状态 s ′ s' s′的概率
• $\mathcal{R}$：奖励函数$\mathcal{R}(s,a)$，表示在状态$s$下采取动作$a$后的奖励。
• $\gamma$：折扣因子$\gamma \in [0,1)$，取值越大越注重长期积累的奖励。

• MDP与MRP的区分
  MDP与马尔可夫奖励过程$MRP=<\mathcal{S},\mathcal{P},r,\gamma >$的区别在于状态转移和奖励函数不依赖于动作$a$。举例：船在海上自由飘荡是一个MRP，船由水手掌舵在海上航行是一个MDP。

1.2 Agent与MDP环境的交互

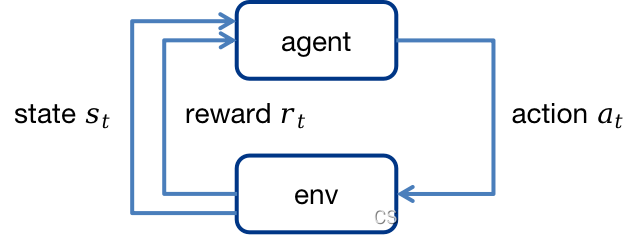
Agent通过 r t r_t rt​学习策略，agent通过学习到的策略针对当前环境状态 s t s_t st​采取相应动作 a t a_t at​，该动作与环境交互后，环境中的状态将转移到新的状态 s t + 1 s_{t+1} st+1​，同时获得奖励 r t + 1 r_{t+1} rt+1​。Agent的目标是最大化累积奖励的期望。

1.2.1 策略policy

策略用$\pi$表示，策略是一个函数，是agent学习的目标。策略会输出在状态$s$下采取各个action的概率，即 π ( a ∣ s ) = P ( A t = a ∣ S t = s ) \pi(a|s)=P(A_t=a|S_t=s) π(a∣s)=P(At​=a∣St​=s).

1.2.2 状态价值函数$V(s)$

V π ( s ) V^\pi(s) Vπ(s)表示从状态$s$出发，采取策略$\pi$获得回报的期望，即
V π ( s ) = E π [ G t ∣ S t = s ] V^\pi(s) = E_\pi[G_t|S_t=s] Vπ(s)=Eπ​[Gt​∣St​=s]

1.2.3 动作价值函数Q(a|s)

Q π ( a ∣ s ) Q^\pi(a|s) Qπ(a∣s)表示MDP遵循策略$\pi$，在状态$s$下采取动作$a$后得到回报的期望，即：
Q π ( a ∣ s ) = E π [ G t ∣ S t = s , A t = a ] Q^\pi(a|s)= E_\pi[G_t|S_t=s,A_t=a] Qπ(a∣s)=Eπ​[Gt​∣St​=s,At​=a]

• V π ( s ) V^\pi(s) Vπ(s) 与 Q π ( a ∣ s ) Q^\pi(a|s) Qπ(a∣s)的关系？
  使用策略$\pi$， V π ( s ) V^\pi(s) Vπ(s) 为采取动作$a$的概率乘在状态$s$下采取动作$a$的动作价值的累加和，即：
  V π ( s ) = ∑ a ∈ A π ( a ∣ s ) Q π ( a ∣ s ) V^\pi(s)=\sum_{a\in \mathcal{A}}\pi(a|s)Q^\pi(a|s) Vπ(s)=a∈A∑​π(a∣s)Qπ(a∣s)

1.2.4 贝尔曼期望方程

V π ( s ) = E π [ G t ∣ S t = s ] = E π [ R t + 1 + γ V π ( s ′ ) ∣ S t = s ] \begin{aligned} V^\pi(s) &= E_\pi[G_t|S_t=s]\\ &=E_\pi[R_{t+1}+\gamma V^\pi(s')|S_t=s]\\ \end{aligned} Vπ(s)​=Eπ​[Gt​∣St​=s]=Eπ​[Rt+1​+γVπ(s′)∣St​=s]​

Q π ( a ∣ s ) = E π [ G t ∣ S t = s , A t = a ] = E π [ R t + 1 + γ Q π ( s t + 1 , a t + 1 ) ∣ S t = s , A t = a ] \begin{aligned} Q^\pi(a|s) &= E_\pi[G_t|S_t=s,A_t=a]\\ &=E_\pi[R_{t+1}+\gamma Q^\pi(s_{t+1},a_{t+1})|S_t=s,A_t=a] \end{aligned} Qπ(a∣s)​=Eπ​[Gt​∣St​=s,At​=a]=Eπ​[Rt+1​+γQπ(st+1​,at+1​)∣St​=s,At​=a]​

其展示了当前状态与未来状态的关联。

由
V π ( s ) = ∑ a ∈ A π ( a ∣ s ) Q π ( a ∣ s ) Q π ( s , a ) = R ( s , a ) + γ ∑ P ( s ′ ∣ s , a ) V π ( s ′ ) V^\pi(s)=\sum_{a\in \mathcal{A}}\pi(a|s)Q^\pi(a|s)\\ Q^\pi(s,a) = R(s,a)+\gamma\sum_{}P(s'|s,a)V^\pi(s') Vπ(s)=a∈A∑​π(a∣s)Qπ(a∣s)Qπ(s,a)=R(s,a)+γ∑​P(s′∣s,a)Vπ(s′)
代入贝尔曼期望方程中，可以得到贝尔曼期望方程的另一种形式：
V π ( s ) = ∑ a ∈ A π ( a ∣ s ) ( R ( s , a ) + γ ∑ s ′ ∈ S P ( s ′ ∣ s , a ) ∑ s ′ ∈ S V π ( s ′ ) ) Q π ( s , a ) = R ( s , a ) + γ ∑ s ′ ∈ S P ( s ′ ∣ s , a ) ∑ a ′ ∈ A π ( a ′ ∣ s ′ ) Q ( s ′ , a ′ ) V^\pi(s)=\sum_{a\in A}\pi(a|s)(R(s,a)+\gamma\sum_{s'\in S}P(s'|s,a)\sum_{s'\in S}V^\pi(s'))\\\ Q^\pi(s,a)=R(s,a)+\gamma\sum_{s'\in S}P(s'|s,a)\sum_{a'\in A}\pi(a'|s')Q(s',a') Vπ(s)=a∈A∑​π(a∣s)(R(s,a)+γs′∈S∑​P(s′∣s,a)s′∈S∑​Vπ(s′)) Qπ(s,a)=R(s,a)+γs′∈S∑​P(s′∣s,a)a′∈A∑​π(a′∣s′)Q(s′,a′)

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！