matlab 二阶导（海森矩阵）的数值计算（附代码和示例）

海森矩阵中就是单值函数对自变量（可以是向量，如 x = [ x 1 , x 2 , x 3 , . . . ] \mathbf{x}=[x_1,x_2,x_3,...] x=[x1​,x2​,x3​,...]）的二阶导数：

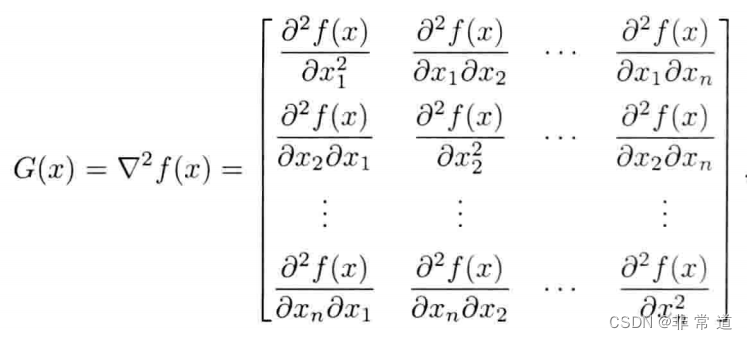
其中元素，如G的第一行第二列元素的定义如下：

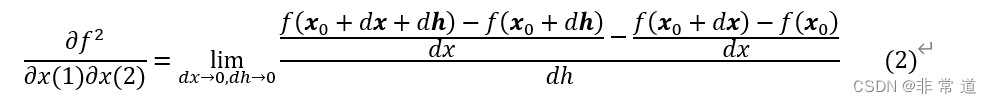
可以看出是两个一阶导数的差再除以一个微小增量。如果$\mathbf{x}$是个二元自变量，那么：

Talk is cheap. Show me the code:

function [H]=hessian_numerical(f,x0,dx,dh)%计算数量场f在x0处的海森矩阵H（数值计算，差分距离dx）仅适用于实数n=length(x0);   H=zeros(n,n);for i=1:nfor j=1:nx1=x0;x1(i)=x1(i)+dx;g2=(f(x1)-f(x0))/dx;%偏导定义x2=x1;x2(j)=x2(j)+dh;x3=x0;x3(j)=x3(j)+dh;g1=(f(x2)-f(x3))/dx;%偏导定义H(i,j)=(g1-g2)/dh;%偏导定义endend
end

如果自变量是复数，而单值函数是实数，那么可以把实部和虚部分开，当做二元函数考虑，分别求二阶偏导，相应代码修改如下：

function [H]=hessian_numerical_CtoR(f,x0,dx,dh)%计算数量场f在x0处的海森矩阵H（数值计算，差分距离dx）实值函数对复数的二阶导n=length(x0);   %% 实数Hr=zeros(n,n);for i=1:nfor j=1:nx1=x0;x1(i)=x1(i)+dx;g2=(f(x1)-f(x0))/dx;%偏导定义x2=x1;x2(j)=x2(j)+dh;x3=x0;x3(j)=x3(j)+dh;g1=(f(x2)-f(x3))/dx;%偏导定义Hr(i,j)=(g1-g2)/dh;%偏导定义endend%% 复数Hi=zeros(n,n);for i=1:nfor j=1:nx1=x0;x1(i)=x1(i)+1i*dx;g2=(f(x1)-f(x0))/dx;%偏导定义x2=x1;x2(j)=x2(j)+1i*dh;x3=x0;x3(j)=x3(j)+1i*dh;g1=(f(x2)-f(x3))/dx;%偏导定义Hi(i,j)=(g1-g2)/dh;%偏导定义endendH=Hr+1i.*Hi;%合成海森矩阵
end

注意此处并没有考虑目标函数是个复变函数，hessian_numerical_CtoR可能存在问题，请谨慎使用。

试一下hessian_numerical函数和已知解析解的对比：

fx =@(x) norm(x,2)^2; %目标函数（标量）
gx=@(x) 2.*x;%梯度解析解
Gx=@(x0) 2.*eye(3);%海森矩阵（二阶导数）解析解
rng(0)
x0=rand(3,1);
Gx_num=hessian_numerical(fx,x0,1e-6,1e-6)%数值计算海森矩阵
Gx_ana=Gx(x0)%海森矩阵解析式

结果表示虽然有些误差，但还是可以接受：

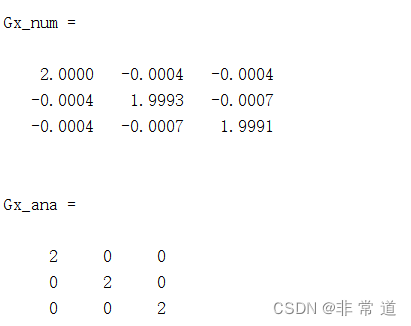
如果把微分量从1e-6调高到1e-3可以解决数值不稳定的问题：

Gx_num=hessian_numerical(fx,x0,1e-3,1e-3)%数值计算海森矩阵

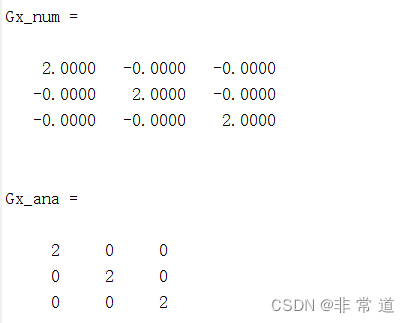
本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！