判断链表是否有环 及 寻找环的入口

1、思路

链表是否有环：使用快慢指针，快指针每次走两步，慢指针每次走一步，如果如果快指针走到了next指针为null时，则链表无环；如果快慢指针相遇，则链表有环。

寻找环的入口：使用快慢指针，快指针每次走两步，慢指针每次走一步；当快慢指针第一次相遇时，将快指针指向链表头部，并且改成每次走一步；下一次快慢指针相遇的位置，就是环入口位置。

2、证明

链表是否有环：

（1）如果链表无环，则快慢指针不会相遇，快指针一定会走到链表的尾部，也就是next指针为null的地方。

（2）如果链表有环，则快慢指针一定会相遇，证明如下：

          当快慢指针都位于环内时，环是不存在先后之分的，我们可以将快慢指针的相遇，当成快指针追赶慢指针的过程，然后用数据归纳法分情况讨论：

          *1）如果快指针位于慢指针后面1位，则下一次走时，慢指针往前走1位，快指针往前走2位，快慢指针相遇。

          *2）如果快指针位于慢指针后面2位，则下一次走时，慢指针往前走1位，快指针往前走2位，变成*1）的情况。

          *3）如果快指针位于慢指针后面n位，则下一次走时，慢指针往前走1位，快指针往前走2位，快指针位于慢指针后面n-1位。
           也就是说，n次后，快慢指针终究会相遇。因为是在环里，快慢指针的距离，一定是小于环的大小的。所以慢指针不用走1圈，就能和快指针相遇。

寻找环的入口：

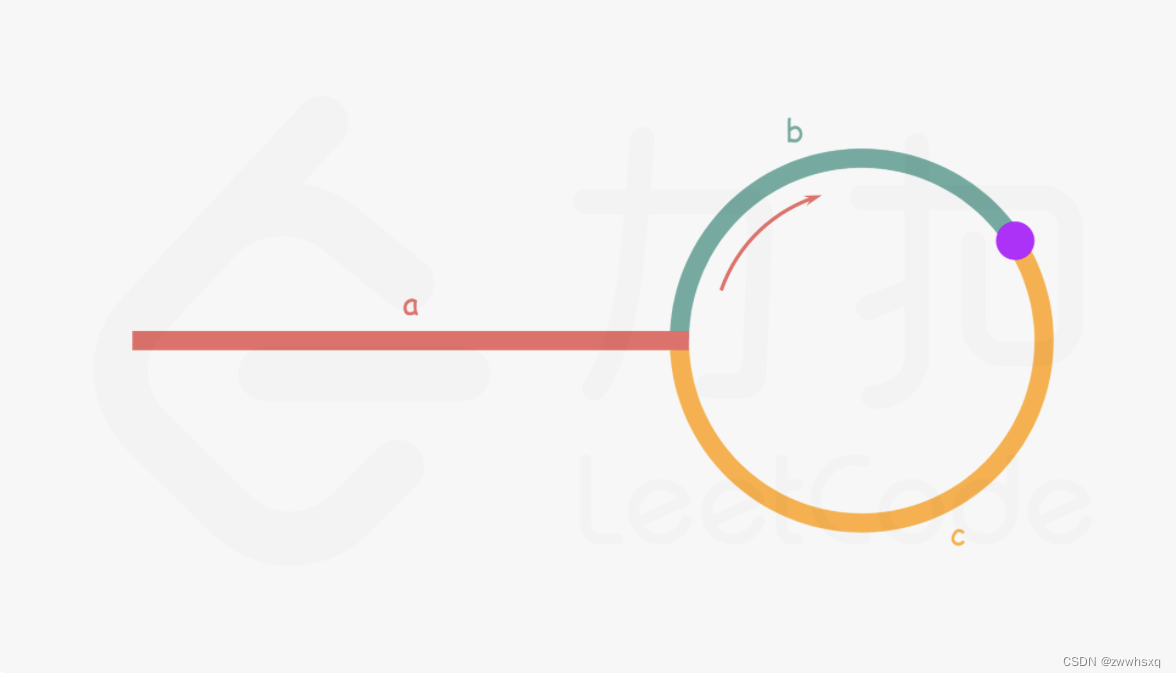
 如上图所示：

             a :  从链表头节点到链表环入口的距离

             b：从链表环入口顺时针到快慢指针第一次相遇的距离

             c： 从快慢指针第一次相遇的位置，顺时针到链表入环点的距离

第一次相遇时，设快指针此时绕环走了N圈，快指针走过的距离是慢指针的2倍：

// 快指针走的距离是慢指针的2倍
2(a + b) = a + N * ( b + c ) + b//上式可以转化为
a = ( N - 1 ) * ( b + c ) + c

a = ( N - 1 ) * ( b + c ) + c，可以理解为：从相遇点到入环点的距离，加上(N-1)圈的环长，刚好等于从链表头部到入环点的距离。

因此，当快慢指针相遇时，我们将快指针指向链表头部，并且改为和慢指针一样，每次走一步，最终它们会在入环扣相遇。
 

3、代码

/*** Definition for singly-linked list.* struct ListNode {*     int val;*     ListNode *next;*     ListNode(int x) : val(x), next(NULL) {}* };*/
class Solution {
public:ListNode *detectCycle(ListNode *head) {ListNode *fast = head;ListNode *slow = head;while (fast != nullptr) {if (fast->next == nullptr) return nullptr;fast = fast->next->next;slow = slow->next;if (fast == slow) {fast = head;while (fast != slow) {fast = fast->next;slow = slow->next;}return fast;}}return nullptr;}
};

 注：本文主要参考：

        *  为什么用快慢指针找链表的环，快指针和慢指针一定会相遇？ - 知乎

        *  力扣

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！