【数据结构笔记16】哈夫曼树，带权路径长度（WPL），哈夫曼编码

本次笔记内容：
5.2.1 什么是哈夫曼树
5.2.2 哈夫曼树的构造
5.2.3 哈夫曼编码

文章目录

• • • 什么是哈夫曼树（Huffman Tree）
    • • 例：将百分制的考试成绩转换为五分制的成绩
      • 哈夫曼树的定义
      • • 带权路径长度（WPL）
        • 最优二叉树或哈夫曼树
    • 哈夫曼树的构造
    • • 思路
      • 实现
    • 哈夫曼树的特点
    • 哈夫曼编码
    • • 例题分析
      • 用前缀码（prefix code）避免二义性
      • 二叉树用于编码
      • 哈夫曼编码例

什么是哈夫曼树（Huffman Tree）

一个ASCII码1个字节，8位，最高位为0。但是造成一些浪费。能不能有一种编码，对于比较频繁出现的信息，用尽量少的位数去表示；不常出现的信息，用大的空间来表示？

例：将百分制的考试成绩转换为五分制的成绩

如上图，这种转换规则（if-else if）对应了一棵判定树。但是如果大部分人的成绩都是81-100分，则都需要判断四次。显然，对于这种情况，该算法不好。

因此考虑学生成绩分布的频率，来进行效率指标的衡量。

原判定树，效率（开销）为3.15。

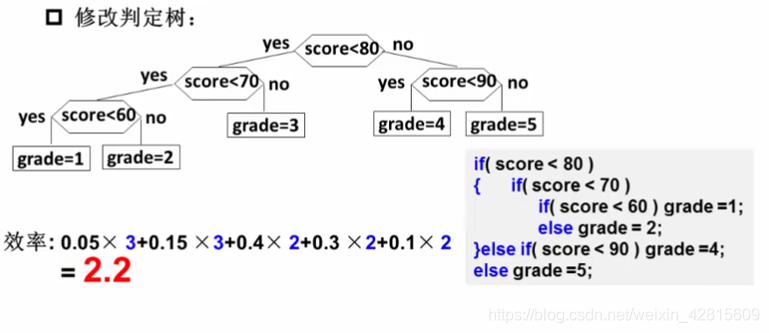
对于修改后的判定树，开销为2.2。显然，比修改前好。

因此，获得启示：如何根据结点不同的查找频率构造更有效的搜索树？

哈夫曼树的定义

带权路径长度（WPL）

Weighted Path Length：设二叉树有$n$个叶子结点，每个叶子结点带有权值 w k w_k wk​，从根结点到每个叶子结点的长度为 l k l_k lk​，则每个叶子结点的带权路径长度之和就是： W P L = ∑ k = 1 n w k l k WPL=\sum_{k=1}^{n}w_k l_k WPL=k=1∑n​wk​lk​

最优二叉树或哈夫曼树

就是WPL最小的二叉树。

如上，不同的二叉树构造方法，二叉树的WPL不同。

哈夫曼树的构造

思路

• 每次把权值最小的两棵二叉树合并。

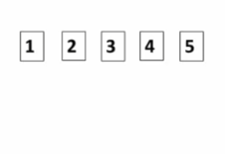
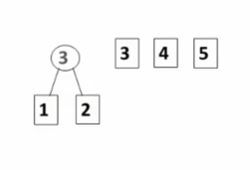
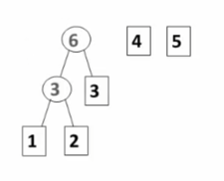
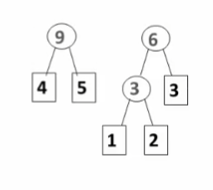
步骤如上，时刻在构造左右子树结点和最小的二叉树。

实现

关键问题在于，如何选取两个最小的？

利用堆！

typedef struct TreeNode *HuffmanTree struct TreeNode
{int Weight;HuffmanTree Left, Right;
};
HuffmanTree Huffman(MinHeap H)
{/* 假设H->Size个权值已经存在H->Elements[]->Weight里 */int i;HuffmanTree T;BulidMinHeap(H); /* 将H->Elements[]按权值调整为最小堆 */for (i = 1; i < H->Size; i++){                                        /* 做H->Size-1次合并 */T = malloc(sizeof(struct TreeNode)); /* 建立新结点 */T->Left = DeleteMin(H);/* 从最小堆中删除根，作为新T的左子节点 */T->Right = DeleteMin(H);/* 从最小堆中删除跟，作为新T的右子结点 */T->Weight = T->Left->Weight + T->Right->Weight;/* 计算新权值 */Insert(H, T);/* 将新T插入最小堆 */}T = DeleteMin(H);return T;
}
// 问题：T是HuffmanTree的实例，怎能直接插入中？不应该是Insert(H,T->Weight)？
// 猜测：或许这里Insert()做了一个重载，作用为插入一个小二叉树。
// 猜测：否定上述猜测，应该写成Insert(H,T->Weight)。
// 问题：这里DeleteMin(H)的用法不对，前两次返回的是数值，最后一次返回的是结点。/*
总结：否定之前的四行问题与猜测。无论是对于Left还是T，都是HuffmanTree的实例，
这里的Insert()、DeleteMin()并非是在“堆”课程中所讲的函数，这里它们的返回值都是
结点，而非数值。
*/

在记笔记过程中发现些问题，总结如上。

此算法的整体复杂度为$$O(NlogN)$$

哈夫曼树的特点

• 没有度为1的结点；
• n个叶子结点的哈夫曼树共有2n-1个结点；
• • n0：叶节点的总数；
• • n1：只有1个儿子的结点总数；
• • n2：有2个儿子的结点总数；
• • n2 = n0 - 1。
• 哈夫曼树的任意非叶结点的左右子树交换后仍是哈夫曼树；
• 对同一组权值{ w 1 , w 2 , . . . , w n w_1,w_2,...,w_n w1​,w2​,...,wn​}，是否存在不同构的两棵哈夫曼树呢？
• • 答案是肯定的，会存在不构同的哈夫曼树，但是WPL都是最小值。

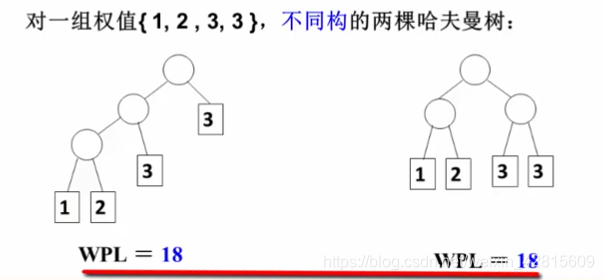
如上图。

哈夫曼编码

• 给定一段字符串，如何对字符进行编码，可以使得该字符串的编码存储空间最少？

例题分析

如上图，本题目与本次笔记开头相呼应。

用前缀码（prefix code）避免二义性

前缀码：任何字符的编码都不是另一字符编码的前缀。可以无二义地解码。

二叉树用于编码

将所有字符都放在二叉树的叶结点上，可以无二义解码。

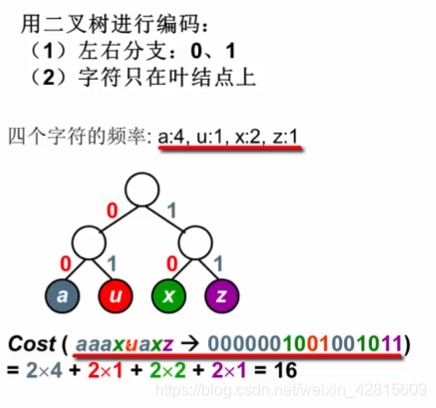
由此，想起哈夫曼树。

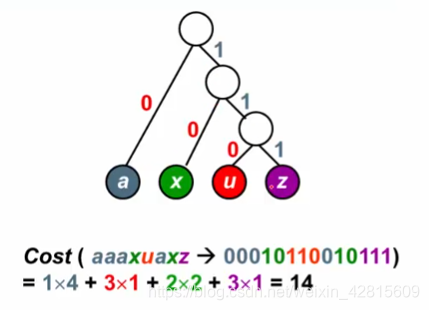
可见，Cost（WPL）小了，使用哈夫曼树效果好。

哈夫曼编码例

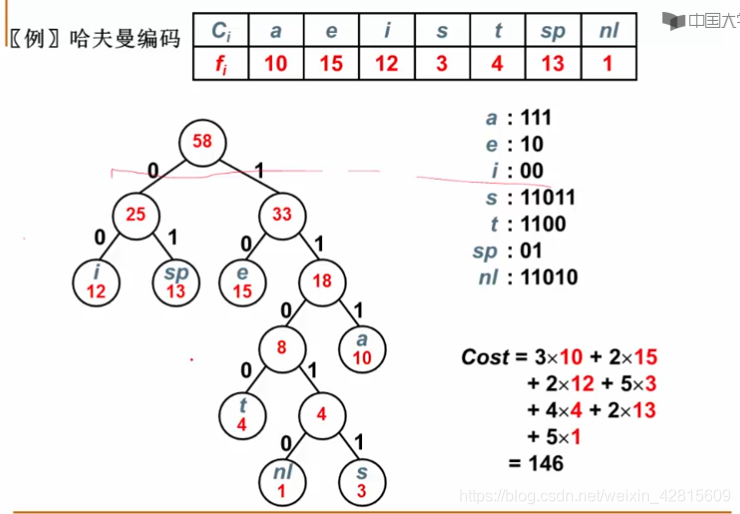
如上图，先根据频率构造哈夫曼树，接着得出每个字符的编码。

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！