【PSO算法学习笔记2】matlab学习之路
接着上篇文章继续,之前记录的是视频课的前面两节课,分别介绍了PSO算法的内容,以及代码设计,虽然这个代码可以实现优化,但是却不够简洁,代码的重复利用度不高。最后一节课就是对基本编码的优化。
代码的优化
前面基础设计,可以看出每次循环问题都有着5个模块,那么是否可以将PSO问题抽离出来,设计成一个函数,这样想要更改问题的参数直接更改函数的参数即可,不用打开代码一个个进行修改。
首先设计一个PSO函数,使其包含问题,和参数属性
function out = PSO (problem,params)
problem中的属性
CostFunction = problem.CostFunction; %目标函数可以更改nVar = problem.nVar; %决策变量的个数VarSize = [1 nVar]; %决策变量的矩阵大小VarMin = problem.VarMin;
VarMax = problem.VarMax; %变量的上下界
params的属性
%% Parameters of PSOMaxIt = params.MaxIt; %最大迭代次数
nPop = params.nPop; %种群个数
w = params.w;
wdamp=params.wdamp; %阻尼惯性系数
c1 = params.c1;
c2 = params.c2; %公式里面的系数
% 在命令行窗口显示迭代信息,true显示,false不显示
ShowIterInfo = params.ShowIterInfo;
%速度的取值范围
MaxVelocity = 0.2*(VarMax-VarMin);
MinVelocity = -MaxVelocity;删除结果显示模块,因为这里PSO是函数,如果要显示结果,直接调用函数后显示。
将PSO函数保存。新建一个pso1.m文件,在这个文件里可以设计想要问题的参数直接调用PSO算法。
pso1中的代码:
- %% Problem Definition :设计PSO函数的problem参数
- %% Parameters of PSO:设计PSO函数的params参数
- %% Calling PSO :调用PSO函数
- %% Results :显示结果
clc;
clear;
close all;%% Problem Definition
problem.CostFunction = @(x) Sphere(x); %目标函数可以更改
problem.nVar = 5; %决策变量的个数
problem.VarMin = -10;
problem.VarMax = 10; %变量的上下界%% Parameters of PSO
params.MaxIt = 100; %最大迭代次数
params.nPop = 100; %种群个数
params.w = 1;
params.wdamp=0.99; %阻尼惯性系数
params.c1 = 2;
params.c2 = 2; %公式里面的系数
params.ShowIterInfo = true; %在命令行窗口显示迭代信息,true显示,false不显示%% Calling PSO
out = PSO(problem,params);
BestCosts=out.BestCosts;
BestSol=out.BestSol ;%% Results
figure;
%plot(BestCosts,"LineWidth",2);
semilogy(BestCosts,"LineWidth",2);
xlabel("Iteration");
ylabel("BestCost");
grid on;运行结果图
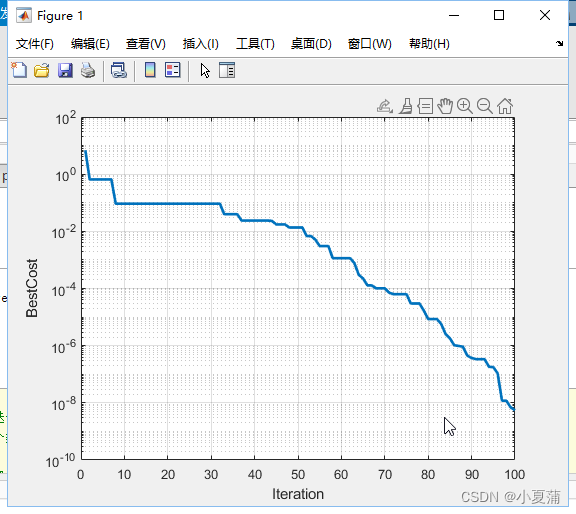
每次迭代之后的结果也要判断是否在取值范围内,避免出现最终的解无法取到,于是在PSO函数循环模块中加入速度的判断和位置的判断:
在速度更新公式后加入:
% 更新后的速度要在范围之内 Apply Velocity Limitsparticle(i).Velocity = max(particle(i).Velocity, MinVelocity);particle(i).Velocity = min(particle(i).Velocity, MaxVelocity);
在位置更新公式后加入:
% 粒子的位置要在规定的范围之内 Apply Lower and Upper Bound Limits%如果粒子的位置低于取值范围之内,则舍去该值,用最小值替代particle(i).Position = max(particle(i).Position, VarMin); particle(i).Position = min(particle(i).Position, VarMax);带收缩系数的PSO模型
可以看出运行结果与之前的结果差不多,但是代码的重复利用度和可读性更高了。
以上被视为标准的PSO算法。为了使PSO算法效果优化,2002年有学者提出了带收缩系数的PSO模型。公式如下:
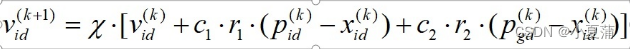

所以要在原先的基础上对算法进一步设计参数。复制pso1.m中的代码,到新建的pso2.m中,在params系数部分添加更新后的部分,
代码如下:
%% Parameters of PSO% 收敛系数,后期学者增加的系数Constriction Coefficients
kappa = 1;
phi1 = 2.05;
phi2 = 2.05;
phi = phi1 + phi2;
chi = 2*kappa/abs(2-phi-sqrt(phi^2-4*phi));params.MaxIt = 100; %最大迭代次数
params.nPop = 100; %种群个数
params.w = chi;
params.wdamp=1; %阻尼惯性系数
params.c1 = chi*phi1;
params.c2 = chi*phi2; %公式里面的系数
params.ShowIterInfo = true; %在命令行窗口显示迭代信息,true显示,false不显示
运行pso2结果如下图所示,迭代的效果图接近直线下降,效果要比之前都要好。
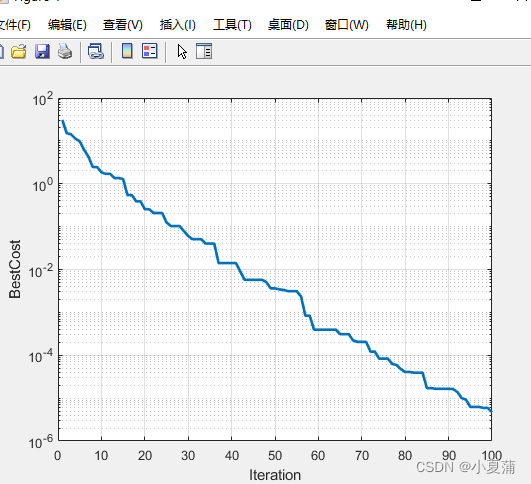
我后面也会将前面的代码文档上传。上一次的笔记代码放在pso_class2.m文件中,上述的所有代码文件都在文件夹中,大家可以免费下载。
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!