线性判别分析 LDA（Linear Discriminant Analysis）

算法目标        

线性判别分析，主要用于分类（Classification）、降维（Dimensionality Reduction）领域。

基本思想是，找到一个单位向量 ，将数据集中的样例映射到  上，使得同类别的样例的投影点尽可能接近，不同类别的样例的投影点尽可能远离。

 如上图所示，比起左侧的映射，右侧的映射更符合我们对 LDA 的期待。

正交投影

正交即垂直，我们来看如何将向量  正交投影到向量  上，及其具体公式是什么。

向量  和  承载了由  向  的这种正交投影关系，所以我们对这种关系，进行计算具象化：

由于向量平行，则 ，

由于向量加减，则  

由于向量垂直，则  ，即

        ​​​​​​​         

那么， 可以重写为：

        ​​​​​​​        

即为，正交投影公式

投影简化

 代表的是被投影的方向。为了简化正交投影公式，我们不妨假设  为单位向量。

单位向量具有性质：

于是正交投影公式被简化为：

这里， 可以看成是  在  方向上的坐标。

对包含  个样例的数据集执行正交投影，可以从  得到  。

这就代表了从  的降维映射。

数据集简化

记数据集为 ，为了简化处理：

假设样例的特征维数为 2，即 

假设样例类别数也为 2，即 

投影点均值

针对数据集中属于  的样例，

记其样例集合为 ，样例个数为 ，投影均值为 ，样本均值为 ，则：

相应的，针对数据集中属于  的样例，有：

抽象点

将针对 “不同类别的样例的投影点尽可能远离” 的数学刻画，描述为最大化两个类别的样例的投影点的均值差，即最大化下式：

将针对 "同类别的样例的投影点尽可能接近" 的数学刻画，描述为最小化类别内部的样例的投影点的方差，即最小化下式子：

Fisher's LDA

我们将上述的这两个思想：

1. 最大化类间投影点均值之间的差值。

2. 最小化类内投影点的方差。

融入到一个定义中，便得到了 Fisher's LDA :

现在，我们的目标转换为：找到一个向量  ，使得目标函数  取得最大值。

所找到的向量  被称为最优线性判别 ( Optimal Linear Discriminant )

将样本数据代入目标函数

这里的  被称为类间散度矩阵（Between class scatter matrix），维度为 

这里的  被称为  的散度矩阵，

同样由  ，可得：

那么，LDA 的目标函数可以重写为：

目标函数求解

目标函数对  求导，令求导后的式子为零，便可求得最优的  值。

1. 回顾一下分数的微分公式：

2. 回顾一下矩阵的微分公式：

3. 同时我们发现 

        ，

所以，令：

即得到：

        ​​​​​​​      

        ​​​​​​​      

注意到，这里  是个 1*1 的值，而不是一个矩阵，得到：

如果  是一个可逆矩阵，那么得到：

        ​​​​​​​     

观察该等式的形式，我们已经将问题转化成了特征值、特征向量的分解问题。

特征向量为 ，对应的特征值为 。

我们要做的，就是对矩阵  进行特征值分解（Eigen Decomposition），然后找到最大特征值所对应的那个特征向量，即为我们要找的最优向量 

针对多分类

相对于二分类而言，多分类在类内散度矩阵 S 上没有变化，只在类间散度矩阵（Between class scatter matrix） 上有如下变化：

这里：

 为多分类的类别数

 为单个类别的样本数

 为单个类别的样本均值

 为所有类别的总体样本均值

代码实现

import numpy as np
from sklearn import datasets
from sklearn import preprocessing
import matplotlib.pyplot as pltclass LDA:"""入口函数@param X: The type of X is np.array @param y: The type of y is np.array"""def fit(self, X, y):self.X = Xself.y = yself.target_classes = np.unique(y)# 每个类别的样本均值self.sub_mean = []for cls in self.target_classes:self.sub_mean.append(np.mean(X[list(y == cls)], axis=0))    # 所有类别的样本均值self.all_mean = np.mean(X, axis=0).reshape(1, X.shape[1])B = self.calculateB()S = self.calculateS()# 计算 S 的逆矩阵，乘以 BS_inv_B = np.linalg.inv(S).dot(B)# 计算对应的特征向量eig_vecs = self.sortEigenVectors(S_inv_B)return eig_vecs"""计算类间散度矩阵 B"""def calculateB(self):B = np.zeros((X.shape[1], X.shape[1]))for cls, mean in enumerate(self.sub_mean):# 每个类别的样本数n = self.X[self.y == cls].shape[0]mui_mu = mean.reshape(1, self.X.shape[1]) - self.all_meanB += n * np.dot(mui_mu.T, mui_mu)return B"""计算类内散度矩阵 S"""def calculateS(self):si_list = []for cls, mean in enumerate(self.sub_mean):si = np.zeros((X.shape[1], X.shape[1]))for xi in X[self.y == cls]:xi_mu = (xi - mean).reshape(1, self.X.shape[1])si += np.dot(xi_mu.T, xi_mu)si_list.append(si)S = np.zeros((X.shape[1], X.shape[1]))for si in si_list:S += sireturn S"""计算最大特征向量"""def sortEigenVectors(self, M):# 计算特征值，特征向量eig_values, eig_vectors = np.linalg.eig(M)# 排序找到最大特征值对应的特征向量idx = eig_values.argsort()[::-1]eig_values = eig_values[idx]eig_vectors = eig_vectors[:,idx]return eig_vectors"""初始化函数"""def __init__(self):pass"""
加载 Iris 数据集
"""
def load_iris_data(cols):iris = datasets.load_iris()X = iris['data']y = iris['target']return X, y# 加载数据
X, y = load_data(None)
X = X[:,(2,3)]
lda = LDA()
eig_vecs = lda.fit(X, y)
W = eig_vecs[:, :1]# 绘制数据
colors = ['red', 'green', 'blue']
fig, ax = plt.subplots(figsize=(10, 8))
for point, pred in zip(X, y):ax.scatter(point[0], point[1], color=colors[pred], alpha=0.3)proj = (np.dot(point, W) * W) / np.dot(W.T, W)ax.scatter(proj[0], proj[1], color=colors[pred], alpha=0.3)
plt.show()

结果展示：

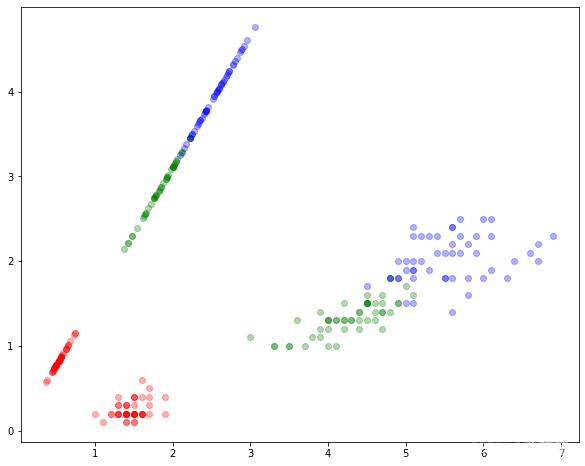
本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！