二叉树的层次遍历

• ★算法思想★
• 1.头文件及元素类型定义
• 2.相关类型定义
• 3.函数声明
• 4.基本操作
• • 4.1 初始化队列
  • 4.2 判空
  • 4.3 入队操作
  • 4.4 出队操作
  • 4.5 先序建立二叉树
  • 4.6 打印结点
  • 4.7 二叉树的层次遍历
  • 4.8 main函数
  • 4.9 测试
  • • 4.9.1 二叉树结构
    • 4.9.2 测试结果
• 5.小结

★算法思想★

1. 初始化一个辅助队列
2. 根结点入队
3. 若队列非空，则队头结点出队，访问该结点，并将其左、右孩子插入队尾（如果有的话）
4. 重复3中的操作直至队列为空

• PS：从上述算法思想中可以看出需要用到的队列相关操作有：初始化队列、判空、入队、出队。

1.头文件及元素类型定义

#include<stdio.h>
#include<stdlib.h>
#define ElemType BiTNode*
#define ElemType1 char

2.相关类型定义

//1.二叉树结点类型定义
typedef struct BiTNode {ElemType1 data;		//结点中的数据域struct BiTNode* lchild, * rchild;	//左右孩子指针
}BiTNode, * BiTree;//2.辅助队列结点类型定义
typedef struct LinkNode {		BiTNode* data;				//存指针而不是结点struct LinkNode* next;		//指向下一个结点的指针
}LinkNode;//3.辅助队列类型定义
typedef struct {				LinkNode* front, * rear;	//队列的队头指针和队尾指针 
}LinkQueue;

3.函数声明

/*函数声明*/
void InitQueue(LinkQueue& Q);				//1.初始化队列
bool LiQueueEmpty(LinkQueue Q);				//2.判空
bool EnQueue(LinkQueue& Q, ElemType x);		//3.入队操作	
bool ExQueue(LinkQueue& Q, ElemType& x);	//4.出队操作
void CreateBiTree(BiTree& T);				//5.先序建立二叉树
void visit(BiTNode* p);						//6.打印结点
void LevelOrder(BiTree T);					//7.二叉树的层次遍历	

4.基本操作

4.1 初始化队列

//1.初始化队列(无头结点)
void InitQueue(LinkQueue& Q) {Q.front = Q.rear = NULL;		//初始化时front、rear都指向NULL
}

4.2 判空

//2.判空(无头结点)
bool LiQueueEmpty(LinkQueue Q) {return (Q.front == NULL);//或者return (Q.rear == NULL);
}

4.3 入队操作

//3.入队操作(无头结点)
bool EnQueue(LinkQueue& Q, ElemType x) {LinkNode* s = (LinkNode*)malloc(sizeof(LinkNode));if (s == NULL)return false;	//内存不足，分配失败s->data = x;		//为新结点赋值s->next = NULL;		//因为新结点只能从队尾插入，即新结点为最后一个结点，其next指针为NULLif (Q.rear == NULL)		//如果当前队列为空，入队结点为第一个结点Q.front = Q.rear = s;	//修改队头和队尾指针else {				//其他结点的插入与带头结点的插入一致Q.rear->next = s;		//新结点插入到rear之后：原先队尾指针所指结点的next指向新结点Q.rear = s;			//修改队尾结点指针，指向新的队尾结点}return true;
}

4.4 出队操作

//4.出队操作(无头结点)
bool ExQueue(LinkQueue& Q, ElemType& x) {if (Q.front == NULL)return false;	//队空，报错LinkNode* p = Q.front;	//找到队头元素x = p->data;				//变量x返回队头元素Q.front = p->next;	//修改队头指针：将队头结点的后继结点赋给队头指针if (Q.rear == p)			//如果此次为最后一个结点出队	Q.rear = Q.front = NULL;		//修改rear指针,队列置空free(p);		//释放结点空间return true;
}

4.5 先序建立二叉树

//5.先序建立二叉树
void CreateBiTree(BiTree& T) {char c;scanf("%c", &c);if (c == '#')T = NULL;else {T = (BiTNode*)malloc(sizeof(BiTNode));T->data = c;CreateBiTree(T->lchild);CreateBiTree(T->rchild);}
}

4.6 打印结点

//6.打印结点-用于遍历
void visit(BiTNode* p) {printf("%c\t", p->data);
}

4.7 二叉树的层次遍历

//7.二叉树的层次遍历
void LevelOrder(BiTree T) {LinkQueue Q;InitQueue(Q);		//初始化辅助队列BiTree p;EnQueue(Q, T);			//根结点入队while (!LiQueueEmpty(Q)) {		//队列不空则循环ExQueue(Q, p);		//队头结点出队visit(p);					//访问出队结点if (p->lchild != NULL)EnQueue(Q, p->lchild);		//左子树不空，则左子树根结点入队if (p->rchild != NULL)EnQueue(Q, p->rchild);		//右子树不空，则右子树根结点入队}
}

4.8 main函数

int main() {BiTree T;			//声明一个二叉树/*1、先序创建二叉树*/printf("先序创建二叉树：");CreateBiTree(T);	//先序建立二叉树/*2、层次遍历*/printf("层次遍历二叉树：");LevelOrder(T);return 0;
}

4.9 测试

4.9.1 二叉树结构

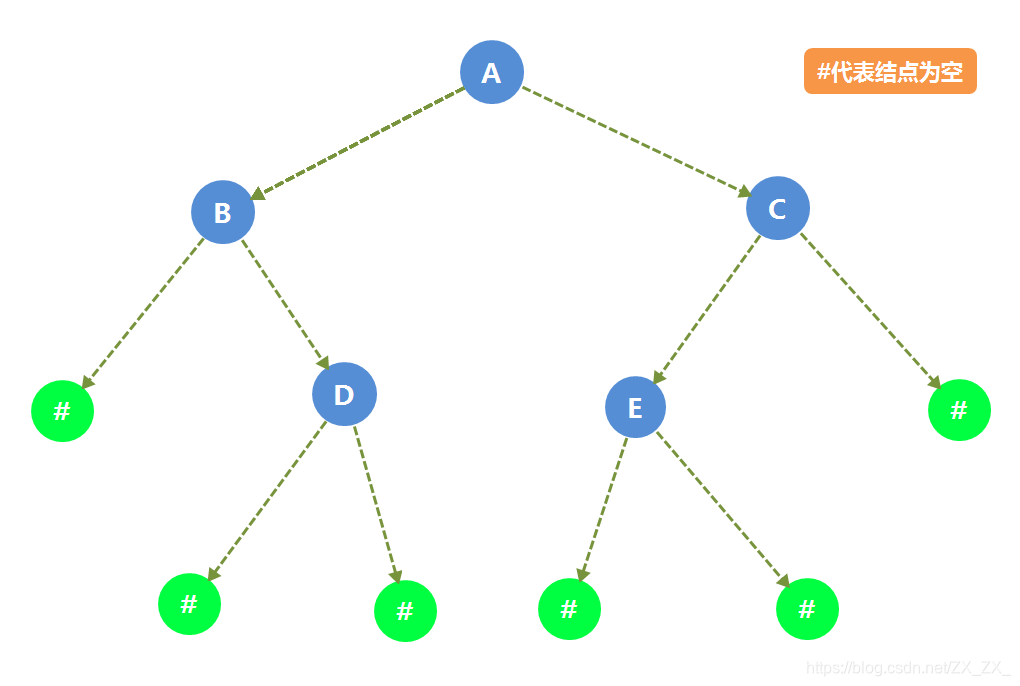
4.9.2 测试结果

5.小结

1. 二叉树的层次遍历与其他三种遍历有所不同，属于广度优先遍历，是队列的具体应用，并且此实现过程是非递归的。
2. 至此，二叉树的遍历操作基本介绍完成。遍历是二叉树的各种操作的基础，可以在遍历的过程中对结点进行各种操作，例如：求结点的双亲、求结点的孩子结点等。所有的这些操作都建立在二叉树遍历的基础上，因此，必须掌握二叉树的各种遍历过程，才能更灵活的解决各种问题。
3. 遍历二叉树后会得到一个线性序列，除第一个结点和最后一个结点外，每个结点都有一个直接前驱和直接后继。但传统的二叉链表仅能体现父子关系，查找结点的前驱和后继是很不方便的。因此，利用“n个结点的二叉链表中，含有n+1个空链域”这一特性，通过这n+1个空指针来存放其前驱或后继的指针，以达到加快查找结点前驱和后继的速度，因此，引入线索二叉树。

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！