二叉树层次遍历--C语言

  之前写了二叉树的先序、中序、后序遍历，这些遍历都用到了栈结构。今天写一下二叉树的层次遍历，层次遍历用到的数据结构是队列。
  层次遍历算法中增加了三个int型数据，其中levelcount用于记录现在处理的是树的第几层；curlevel用于记录当前层还有几个节点没有被访问过；nextlevel用于记录本层的下一层的节点数。
代码如下：

#include "stdafx.h"
#include "stdio.h"
#include "stdlib.h"
#define INITQUEUE 20typedef struct BiTNode
{char data;//节点数据struct BiTNode *lchild;//节点左孩子指针struct BiTNode *rchild;//节点右孩子指针
}BiTNode,*BiTree;//二叉树节点typedef struct Queue
{BiTNode *front;//队列头指针BiTNode *tail;//队列尾指针int size;//队列空间大小
}Queue;//创建队列
int InitQueue(Queue &Q)
{Q.front = (BiTNode*)malloc(INITQUEUE * sizeof(BiTNode));if(!Q.front){return 0;}Q.tail = Q.front;Q.size = INITQUEUE;return 1;
}//判断队列是否为空
bool EmptyQueue(Queue Q)
{if(Q.tail == Q.front){return true;}else{return false;}
}//入队列
int EnQueue(Queue &Q,BiTNode e)
{if((Q.tail - Q.front + INITQUEUE) % INITQUEUE == INITQUEUE - 1){return 0;}*Q.tail = e;Q.tail++;return 1;
}//出队列
int DeQueue(Queue &Q,BiTNode &e)
{if(Q.front == Q.tail){return 0;}e = *Q.front;Q.front++;return 1;
}//创建二叉树
void CreateBiTree(BiTree &T)
{char ch;scanf("%c",&ch);if('#' == ch){T = NULL;}else{T = (BiTree)malloc(sizeof(BiTNode));T->data = ch;CreateBiTree(T->lchild);CreateBiTree(T->rchild);}
}//二叉树的层次遍历
int levelTraverse(BiTree T)
{if(NULL == T){return 0;}BiTNode e;Queue Q;int levelcount = 0;//树的深度int curlevel = 1;//本层剩余的未访问的节点数int nextlevel = 0;//下一层未访问的节点数InitQueue(Q);EnQueue(Q,*T);while(!EmptyQueue(Q)){DeQueue(Q,e);printf("%c ",e.data);curlevel--;if(NULL != e.lchild){EnQueue(Q,*e.lchild);nextlevel ++;}if(NULL != e.rchild){EnQueue(Q,*e.rchild);nextlevel++;}if(0 == curlevel){levelcount++;printf("第%d层节点遍历结束!\n",levelcount);curlevel = nextlevel;nextlevel =0;}}return 1;
}int main(int argc, char* argv[])
{BiTree T = NULL;CreateBiTree(T);levelTraverse(T);return 0;
}

二叉树的结构为：

遍历结果：

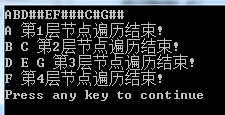
  二叉树的遍历基本上已经写过一遍了，有机会需要写一个二叉树的总结。当然现在写的都还只是二叉树的皮毛的东西，像二叉树的一些应用（平衡二叉树、红黑树等）都还没有写。但是这些东西需要先把理论弄清楚，才能着手去写，要不然思路不清晰，写出来的代码必然是不能看的！

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！