python 求点和点之间的距离;向量之间的余弦距离、欧式距离;点到向量的距离
据说五一期间发文会有五一创作勋章,正好最近需要这份总结。
本文打算不讲述原理,数学原理采用链接的方式提供,主要介绍实现方法和其用到的函数。
目录
- 1. 点和点之间的距离
- 方法一:利用数学公式
- 方法二:向量的内积
- 方法三:范数函数
- 2. 向量之间的余弦距离
- 3. 向量之间的欧式距离
- 方法一:数学原理
- 方法二:其他
- 4. 点到向量的距离
- 方法一:利用向量计算点到直线的距离
以下所有的计算是基于笛卡尔坐标系,点的位置信息用array进行存储。
1. 点和点之间的距离
方法一:利用数学公式
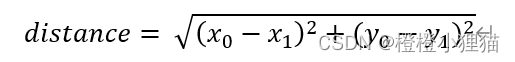
import numpy as np
import mathpoint0 = np.array([2, 2])
point1 = np.array([1, 1])
distance = math.sqrt(math.pow(point0[0] - point1[0], 2) + math.pow(point0[1] - point1[1], 2))
print(distance) ## 1.4142135623730951方法二:向量的内积
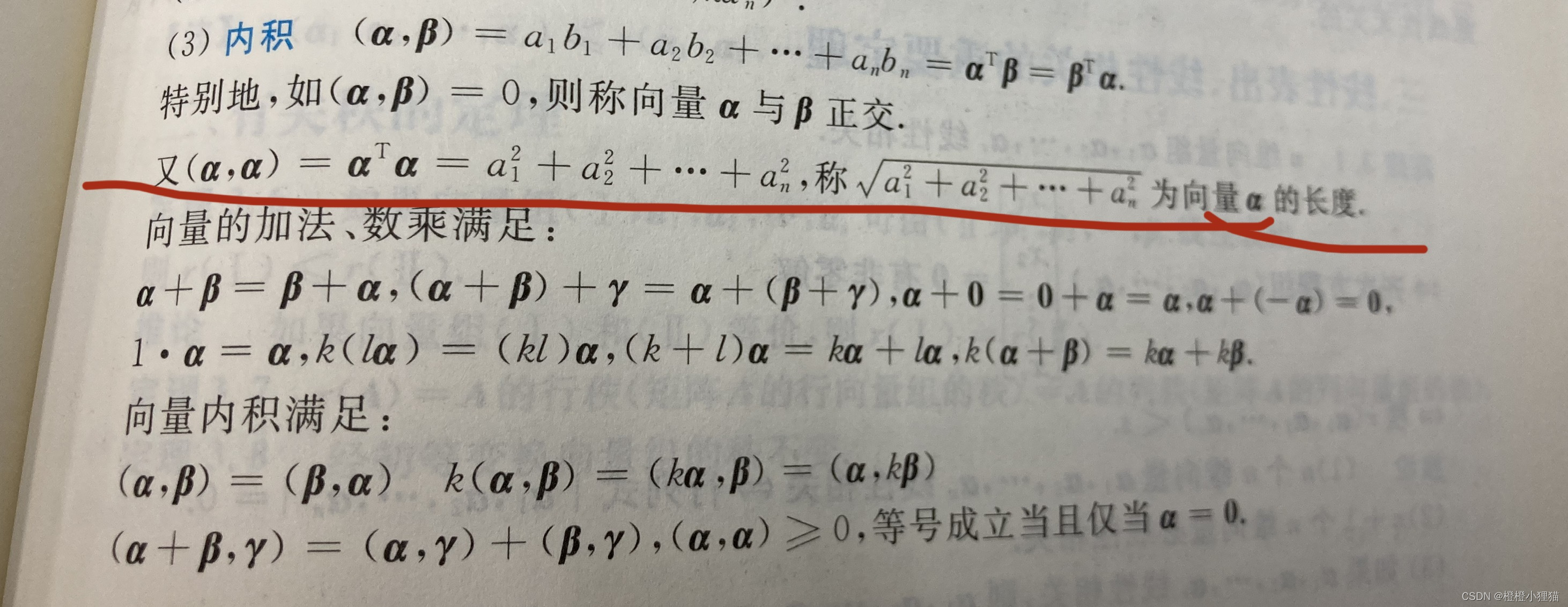
import numpy as nppoint0 = np.array([2, 2])
point1 = np.array([1, 1])
v1 = point0 - point1
distance = np.sqrt(np.sum(v1 * v1))
print(distance) ## 1.4142135623730951方法三:范数函数
| 所用函数名 | 参考网址 |
|---|---|
np.linalg.norm(x, ord=None, axis=None, keepdims=False) | 官网、np.linalg.norm()用法总结 |
import numpy as nppoint0 = np.array([2, 2])
point1 = np.array([1, 1])
distance1 = np.linalg.norm(point0 - point1)
print(distance1) ## 1.4142135623730951
python中numpy数组和矩阵的乘法
2. 向量之间的余弦距离
什么是余弦距离?余弦距离
| 所用函数名 | 参考网址 | 说明 |
|---|---|---|
np.dot(a, b[, out]) | 两个数组的点积,数组必须相同维度 | |
np.arccos(x[, out]) | 求其反余弦值 |
import numpy as np# 余弦距离计算角度[0-180)
def get_angle(v1, v2):# 如果其中一个是零向量则直接返回if np.count_nonzero(v1) == 0 or np.nonzero(v2) == 0:return np.nan# 求其余弦距离angle = np.dot(v1, v2) / (np.sqrt(np.sum(v1 * v1)) * np.sqrt(np.sum(v2 * v2)))# 转换成向量之间的角度angle = np.arccos(angle) / np.pi * 180return anglepoint0 = np.array([2, 2])
point1 = np.array([1, 1])
point3 = np.array([1, 0])
point4 = np.array([0, 0])# 组成向量
vv1 = point0 - point1
vv2 = point3 - point4
print(vv1 * vv2) ## [1 0]
print(get_angle(vv1, vv2)) ## 45.000000000000013. 向量之间的欧式距离
什么是欧式距离?计算两个向量间的欧氏距离_计算字符串距离
方法一:数学原理
import numpy as np
import mathdef euclidean_distance(v1, v2):return math.sqrt(math.pow((v2[0] - v1[0]), 2) + math.pow((v2[1] - v1[1]), 2))point0 = np.array([2, 2])
point1 = np.array([1, 1])
point3 = np.array([1, 0])
point4 = np.array([0, 0])vv1 = point0 - point1
vv2 = point3 - point4
print(euclidean_distance(vv1, vv2))方法二:其他
Python:计算两个向量的欧式距离
import numpy as npa = np.array([1,2,3,6])
b = np.array([3,2,1,5])def dist(a, b):return np.sqrt(sum((a - b) ** 2))print(dist(a,b))print(np.linalg.norm(a-b,ord=2))4. 点到向量的距离
方法一:利用向量计算点到直线的距离
原理
Python计算点到直线距离的两种方法
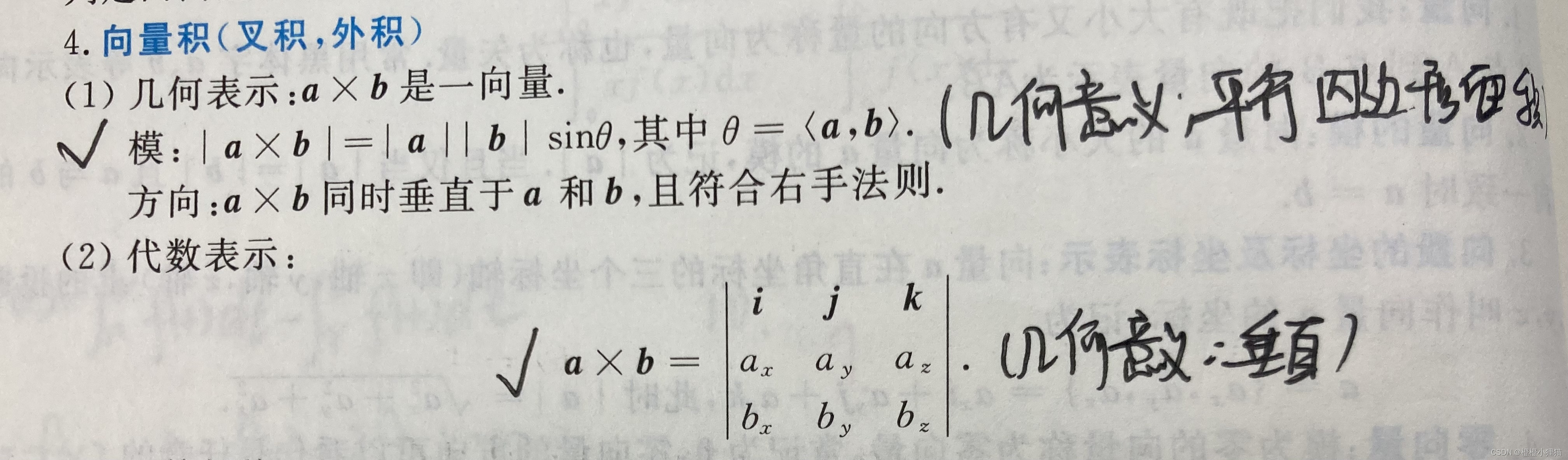
函数
| 所用函数名 | 参考网址 | 说明 |
|---|---|---|
np.cross(a, b, axisa=-1, axisb=-1, axisc=-1, axis=None) | 计算两个向量(向量数组)的叉乘。 |
代码
import numpy as npdef get_dot_line_distance(point, line_point1, line_point2):v1 = line_point1 - pointv2 = line_point2 - pointdistance = np.abs(np.cross(v1, v2)) / np.linalg.norm(line_point1 - line_point2)return distancepoint0 = np.array([2, 2])
point1 = np.array([1, 1])
point3 = np.array([1, 0])
point4 = np.array([0, 0])vv1 = point0 - point1
vv2 = point3 - point4print(get_dot_line_distance(point3, point0, point1)) ## 0.7071067811865475本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!