时间复杂度递归方程求解

简介

1.迭代法/Iteration方法

——把方程转化成一个和式

——然后用估计和的方法来求解

2.Master方法

——求解形为T(n)=aT(n/b)+f(n)的递归方程

迭代法/Iteration方法

1.不断用递归方程的右部替换左部

2.每次替换，随着n的降低，在和式中多出一项

3.直到出现初值，停止迭代

4.将初值代入并对和式求和

5.可用数学归纳法验证解的正确性

例题1：求n!

int fact(int n)
{if(n==0||n==1)return 1;elsereturn n*fact(n-1);
}

条件：

T(1)=1;

T(n)=T(n-1)+1;

解答：

T(n)=T(n-1)+1=T(n-2)+2=T(n-3)+3=......=T(1)+n-1=n=O(n)

例2：设n=2^k，T(1)=1，求T(n)=2T(n/2)+2的渐近阶

T(n)=2T(n/2)+2

=2(2T(n/4)+2)+2

=4T(n/4)+4+2

=4(2T(n/8)+2)+4+2

=8T(n/8)+8+4+2

=2^kT(n/2^k)+2^k+......+2

=2^k+2^k+......2

=2^k+2^(k+1)-2

=3n-2

=O(n)

例3：Hanoi塔算法T(n)=2T(n-1)+1 T(1)=1

T(n)=2T(n-1)+1

        =2(2T(n-2)+1)+1

        =4T(n-2)+2+1

        =4(2T(n-3)+1)+2+1

        =8T(n-3)+4+2+1

        =2^(n-1)+2^(n-2)+......1

        =2^n-1

迭代法总结：

有一个式子T(n)=aT(m)+b

和一个终止条件T(k)=z

然后就可以使用迭代法进行求解

Master方法

目的：求解T(n)=aT(n/b)+f(n)型方程，a>=1,b>0是常数，f(n)是正函数。

a:归约后的子问题个数

n/b:归约后的子问题规模

f(n):规约过程及组合子问题的解的工作量

1.在第一种情况下，f(n)不仅要小于，而且必须多项式地小于。

2.在第二种情况下，f(n)不仅要大于，而且必须多项式地大于。

例1：求解T(n)=9T(n/3)+n(第一种情况）

n^log=n^2

n^log>f(n)

T(n)=(n^2)

例2：求解T(n)=T(2n/3)+1（第三种情况）

n^log=1

n^log=f(n)

T(n)=(lgn)

例3:求解T(n)=3T(n/4)+nlgn(第二种情况）

n^log

n^log

T(n)=(nlgn)

例4:求解T(n)=2T(n/2)+nlgn

讨论：时间复杂性和空间复杂性的关系？举例说明时间复杂性和空间复杂性之间的联系。

  复杂度分为时间复杂度和空间复杂度。时间复杂度定性描述该算法的运行时间，空间复杂度是对一个算法在运行过程中临时占用存储空间大小的量度。时间复杂度和空间复杂度在一起衡量一个算法的效率，在时间复杂度在衡量算法效率中更受重视。我们在设计算法的过程中，也有用空间换时间和用时间换空间的说法，一般情况下是要在运算速度和空间资源之间找一个平衡。

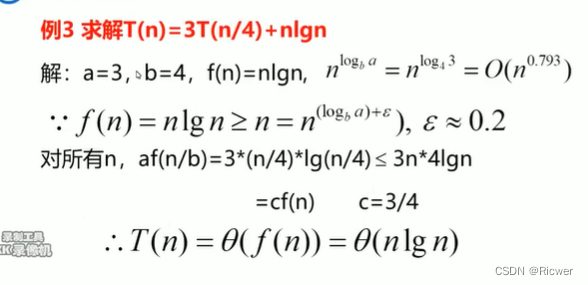
本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！