目录

一、决策树概述

1.1 决策树的概念

1.2 决策树的步骤

1.3 决策树的优缺点

二、决策树的创建

2.1 决策树的一般流程

2.2.典型算法

2.3.构造方法

三、决策树代码实例（ID3）

1.数据集

2、计算经验熵（香农熵）

3、计算信息增益

4、树的生成

5、树的深度和广度计算

6、未知数据的预测

7、树的存储与读取（以二进制形式存储）

8、完整代码

9、运行结果

一、决策树概述

1.1 决策树的概念

        决策树（decision tree）是一种基本的分类与回归方法。决策树模型呈树形结构，在分类问题中，表示基于特征对实例进行分类的过程。它可以认为是if-then规则的集合，也可以认为是定义在特征空间与类空间上的条件概率分布。

        决策树是一种描述对实例进行分类的树形结构，其中每个内部节点表示一个属性上的判断，每个分支代表一个判断结果的输出，最后每个叶节点代表一种分类结果，本质是一颗由多个判断节点组成的树。分类决策树模型是一种树形结构。 决策树由结点和有向边组成。结点有两种类型：内部结点和叶节点。内部结点表示一个特征或属性，叶节点表示一个类。

1.2 决策树的步骤

决策树通常有三个步骤：特征选择、决策树的生成、决策树的修剪。

• 特征选择：从训练数据的特征中选择一个特征作为当前节点的分裂标准（特征选择的标准不同产生了不同的特征决策树算法）。
• 决策树生成：根据所选特征评估标准，从上至下递归地生成子节点，直到数据集不可分则停止决策树停止声场。
• 决策树剪枝：决策树容易过拟合，需要剪枝来缩小树的结构和规模（包括预剪枝和后剪枝）。

        决策树学习的本质是从训练数据集中归纳出一组分类规则或者说是条件概率模型，与训练数据集不相矛盾的决策树可能有多个或者一个没有，我们需要找到一个与训练数据集矛盾较小的决策树，同时具有很好的泛化能力。换句话说，我们选择的条件概率模型应该不仅对现有的训练数据集有很好的拟合效果，而且能够对未知的数据有很好的预测（泛化能力）。实现的方法通过以上的三个方法。

1.3 决策树的优缺点

优点：

• 计算复杂度不高，输出结果易理解，对中间值缺失不敏感，可以处理不相关特征数据。
• 准确性高: 挖掘出来的分类规则准确性高, 便于理解, 决策树可以清晰的显示哪些字段比较重要, 即可以生成可以理解的规则。
• 可以处理连续和离散字段、不需要任何领域知识和参数假设、适合高维数据。

缺点：

• 对于各类别样本数量不一致的数据, 信息增益偏向于那些更多数值的特征。
• 容易过拟合、忽略属性之间的相关性。

适用数据类型：数值型和标称型

二、决策树的创建

2.1 决策树的一般流程

(1) 收集数据：可以使用任何方法。
(2) 准备数据：树构造算法只是用于标称型数据，因此数值型数据必须离散化。
(3) 分析数据：可以使用任何方法，决策树构造完成后，可以检查决策树图形是否符合预期。
(4) 训练算法：构造一个决策树的数据结构。
(5) 测试算法：使用经验树计算错误率。当错误率达到可接收范围，此决策树就可投放使用。
(6) 使用算法：此步骤可以使用适用于任何监督学习算法，而使用决策树可以更好地理解数据的内在含义。

2.2.典型算法

决策树的典型算法有ID3，C4.5，CART等。

国际权威的学术组织，数据挖掘国际会议ICDM （the IEEE International Conference on Data Mining）在2006年12月评选出了数据挖掘领域的十大经典算法中，C4.5算法排名第一。C4.5算法是机器学习算法中的一种分类决策树算法,其核心算法是ID3算法。C4.5算法产生的分类规则易于理解，准确率较高。不过在构造树的过程中，需要对数据集进行多次的顺序扫描和排序，在实际应用中因而会导致算法的低效。

2.3.构造方法

决策树构造的输入是一组带有类别标记的例子，构造的结果是一棵二叉树或多叉树。二叉树的内部节点(非叶子节点)一般表示为一个逻辑判断，如形式为a=aj的逻辑判断，其中a是属性，aj是该属性的所有取值：树的边是逻辑判断的分支结果。多叉树(ID3)的内部结点是属性，边是该属性的所有取值，有几个属性值就有几条边。树的叶子节点都是类别标记。 [3]

由于数据表示不当、有噪声或者由于决策树生成时产生重复的子树等原因，都会造成产生的决策树过大。因此，简化决策树是一个不可缺少的环节。寻找一棵最优决策树，主要应解决以下3个最优化问题：①生成最少数目的叶子节点；②生成的每个叶子节点的深度最小；③生成的决策树叶子节点最少且每个叶子节点的深度最小。

三、决策树代码实例（ID3）

1.数据集

dataSet=[[0, 0, 0, 0, 'no'],[0, 0, 0, 1, 'no'],[0, 1, 0, 1, 'yes'],[0, 1, 1, 0, 'yes'],[0, 0, 0, 0, 'no'],[1, 0, 0, 0, 'no'],[1, 0, 0, 1, 'no'],[1, 1, 1, 1, 'yes'],[1, 0, 1, 2, 'yes'],[1, 0, 1, 2, 'yes'],[2, 0, 1, 2, 'yes'],[2, 0, 1, 1, 'yes'],[2, 1, 0, 1, 'yes'],[2, 1, 0, 2, 'yes'],[2, 0, 0, 0, 'no']]labels=['年龄','有工作','有自己的房子','信贷情况']

2、计算经验熵（香农熵）

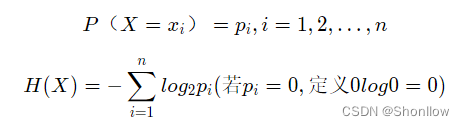
from math import log
def calcShannonEnt(dataSet):# 统计数据数量numEntries = len(dataSet)# 存储每个label出现次数label_counts = {}# 统计label出现次数for featVec in dataSet:current_label = featVec[-1]if current_label not in label_counts:  # 提取label信息label_counts[current_label] = 0  # 如果label未在dict中则加入label_counts[current_label] += 1  # label计数shannon_ent = 0  # 经验熵# 计算经验熵for key in label_counts:prob = float(label_counts[key]) / numEntriesshannon_ent -= prob * log(prob, 2)return shannon_ent

3、计算信息增益

g(D,A)=H(D)−H(D∣A)

def splitDataSet(data_set, axis, value):ret_dataset = []for feat_vec in data_set:if feat_vec[axis] == value:reduced_feat_vec = feat_vec[:axis]reduced_feat_vec.extend(feat_vec[axis + 1:])ret_dataset.append(reduced_feat_vec)return ret_datasetdef chooseBestFeatureToSplit(dataSet):# 特征数量num_features = len(dataSet[0]) - 1# 计算数据香农熵base_entropy = calcShannonEnt(dataSet)# 信息增益best_info_gain = 0.0# 最优特征索引值best_feature = -1# 遍历所有特征for i in range(num_features):# 获取dataset第i个特征feat_list = [exampel[i] for exampel in dataSet]# 创建set集合，元素不可重合unique_val = set(feat_list)# 经验条件熵new_entropy = 0.0# 计算信息增益for value in unique_val:# sub_dataset划分后的子集sub_dataset = splitDataSet(dataSet, i, value)# 计算子集的概率prob = len(sub_dataset) / float(len(dataSet))# 计算经验条件熵new_entropy += prob * calcShannonEnt(sub_dataset)# 信息增益info_gain = base_entropy - new_entropy# 打印每个特征的信息增益print("第%d个特征的信息增益为%.3f" % (i, info_gain))# 计算信息增益if info_gain > best_info_gain:# 更新信息增益best_info_gain = info_gain# 记录信息增益最大的特征的索引值best_feature = iprint("最优索引值：" + str(best_feature))print()return best_feature

4、树的生成

import operator
def majority_cnt(class_list):class_count = {}# 统计class_list中每个元素出现的次数for vote in class_list:if vote not in class_count:class_count[vote] = 0class_count[vote] += 1# 根据字典的值降序排列sorted_class_count = sorted(class_count.items(), key=operator.itemgetter(1), reverse=True)return sorted_class_count[0][0]def creat_tree(dataSet, labels, featLabels):# 取分类标签(是否放贷：yes or no)class_list = [exampel[-1] for exampel in dataSet]# 如果类别完全相同则停止分类if class_list.count(class_list[0]) == len(class_list):return class_list[0]# 遍历完所有特征时返回出现次数最多的类标签if len(dataSet[0]) == 1:return majority_cnt(class_list)# 选择最优特征best_feature = chooseBestFeatureToSplit(dataSet)# 最优特征的标签best_feature_label = labels[best_feature]featLabels.append(best_feature_label)# 根据最优特征的标签生成树my_tree = {best_feature_label: {}}# 删除已使用标签del(labels[best_feature])# 得到训练集中所有最优特征的属性值feat_value = [exampel[best_feature] for exampel in dataSet]# 去掉重复属性值unique_vls = set(feat_value)for value in unique_vls:my_tree[best_feature_label][value] = creat_tree(splitDataSet(dataSet, best_feature, value), labels, featLabels)return my_tree

5、树的深度和广度计算

def get_num_leaves(my_tree):num_leaves = 0first_str = next(iter(my_tree))second_dict = my_tree[first_str]for key in second_dict.keys():if type(second_dict[key]).__name__ == 'dict':num_leaves += get_num_leaves(second_dict[key])else:num_leaves += 1return num_leavesdef get_tree_depth(my_tree):max_depth = 0       # 初始化决策树深度firsr_str = next(iter(my_tree))     # python3中myTree.keys()返回的是dict_keys,不在是list,所以不能使用myTree.keys()[0]的方法获取结点属性，可以使用list(myTree.keys())[0]second_dict = my_tree[firsr_str]    # 获取下一个字典for key in second_dict.keys():if type(second_dict[key]).__name__ == 'dict':     # 测试该结点是否为字典，如果不是字典，代表此结点为叶子结点this_depth = 1 + get_tree_depth(second_dict[key])else:this_depth = 1if this_depth > max_depth:max_depth = this_depth      # 更新层数return max_depth

6、未知数据的预测

def classify(input_tree, feat_labels, test_vec):# 获取决策树节点first_str = next(iter(input_tree))# 下一个字典second_dict = input_tree[first_str]feat_index = feat_labels.index(first_str)for key in second_dict.keys():if test_vec[feat_index] == key:if type(second_dict[key]).__name__ == 'dict':class_label = classify(second_dict[key], feat_labels, test_vec)else:class_label = second_dict[key]return class_label

7、树的存储与读取（以二进制形式存储）

import pickle
def storeTree(input_tree, filename):# 存储树with open(filename, 'wb') as fw:pickle.dump(input_tree, fw)def grabTree(filename):# 读取树fr = open(filename, 'rb')return pickle.load(fr)

8、完整代码

from math import log
import operator
import pickledef calcShannonEnt(dataSet):# 统计数据数量numEntries = len(dataSet)# 存储每个label出现次数label_counts = {}# 统计label出现次数for featVec in dataSet:current_label = featVec[-1]if current_label not in label_counts:  # 提取label信息label_counts[current_label] = 0  # 如果label未在dict中则加入label_counts[current_label] += 1  # label计数shannon_ent = 0  # 经验熵# 计算经验熵for key in label_counts:prob = float(label_counts[key]) / numEntriesshannon_ent -= prob * log(prob, 2)return shannon_entdef splitDataSet(data_set, axis, value):ret_dataset = []for feat_vec in data_set:if feat_vec[axis] == value:reduced_feat_vec = feat_vec[:axis]reduced_feat_vec.extend(feat_vec[axis + 1:])ret_dataset.append(reduced_feat_vec)return ret_datasetdef chooseBestFeatureToSplit(dataSet):# 特征数量num_features = len(dataSet[0]) - 1# 计算数据香农熵base_entropy = calcShannonEnt(dataSet)# 信息增益best_info_gain = 0.0# 最优特征索引值best_feature = -1# 遍历所有特征for i in range(num_features):# 获取dataset第i个特征feat_list = [exampel[i] for exampel in dataSet]# 创建set集合，元素不可重合unique_val = set(feat_list)# 经验条件熵new_entropy = 0.0# 计算信息增益for value in unique_val:# sub_dataset划分后的子集sub_dataset = splitDataSet(dataSet, i, value)# 计算子集的概率prob = len(sub_dataset) / float(len(dataSet))# 计算经验条件熵new_entropy += prob * calcShannonEnt(sub_dataset)# 信息增益info_gain = base_entropy - new_entropy# 打印每个特征的信息增益print("第%d个特征的信息增益为%.3f" % (i, info_gain))# 计算信息增益if info_gain > best_info_gain:# 更新信息增益best_info_gain = info_gain# 记录信息增益最大的特征的索引值best_feature = iprint("最优索引值：" + str(best_feature))print()return best_featuredef majority_cnt(class_list):class_count = {}# 统计class_list中每个元素出现的次数for vote in class_list:if vote not in class_count:class_count[vote] = 0class_count[vote] += 1# 根据字典的值降序排列sorted_class_count = sorted(class_count.items(), key=operator.itemgetter(1), reverse=True)return sorted_class_count[0][0]def creat_tree(dataSet, labels, featLabels):# 取分类标签(是否放贷：yes or no)class_list = [exampel[-1] for exampel in dataSet]# 如果类别完全相同则停止分类if class_list.count(class_list[0]) == len(class_list):return class_list[0]# 遍历完所有特征时返回出现次数最多的类标签if len(dataSet[0]) == 1:return majority_cnt(class_list)# 选择最优特征best_feature = chooseBestFeatureToSplit(dataSet)# 最优特征的标签best_feature_label = labels[best_feature]featLabels.append(best_feature_label)# 根据最优特征的标签生成树my_tree = {best_feature_label: {}}# 删除已使用标签del(labels[best_feature])# 得到训练集中所有最优特征的属性值feat_value = [exampel[best_feature] for exampel in dataSet]# 去掉重复属性值unique_vls = set(feat_value)for value in unique_vls:my_tree[best_feature_label][value] = creat_tree(splitDataSet(dataSet, best_feature, value), labels, featLabels)return my_treedef get_num_leaves(my_tree):num_leaves = 0first_str = next(iter(my_tree))second_dict = my_tree[first_str]for key in second_dict.keys():if type(second_dict[key]).__name__ == 'dict':num_leaves += get_num_leaves(second_dict[key])else:num_leaves += 1return num_leavesdef get_tree_depth(my_tree):max_depth = 0       # 初始化决策树深度firsr_str = next(iter(my_tree))     # python3中myTree.keys()返回的是dict_keys,不在是list,所以不能使用myTree.keys()[0]的方法获取结点属性，可以使用list(myTree.keys())[0]second_dict = my_tree[firsr_str]    # 获取下一个字典for key in second_dict.keys():if type(second_dict[key]).__name__ == 'dict':     # 测试该结点是否为字典，如果不是字典，代表此结点为叶子结点this_depth = 1 + get_tree_depth(second_dict[key])else:this_depth = 1if this_depth > max_depth:max_depth = this_depth      # 更新层数return max_depthdef classify(input_tree, feat_labels, test_vec):# 获取决策树节点first_str = next(iter(input_tree))# 下一个字典second_dict = input_tree[first_str]feat_index = feat_labels.index(first_str)for key in second_dict.keys():if test_vec[feat_index] == key:if type(second_dict[key]).__name__ == 'dict':class_label = classify(second_dict[key], feat_labels, test_vec)else:class_label = second_dict[key]return class_labeldef storeTree(input_tree, filename):# 存储树with open(filename, 'wb') as fw:pickle.dump(input_tree, fw)def grabTree(filename):# 读取树fr = open(filename, 'rb')return pickle.load(fr)if __name__ == "__main__":# 数据集dataSet = [[0, 0, 0, 0, 'no'],[0, 0, 0, 1, 'no'],[0, 1, 0, 1, 'yes'],[0, 1, 1, 0, 'yes'],[0, 0, 0, 0, 'no'],[1, 0, 0, 0, 'no'],# [1, 0, 0, 0, 'yes'],[1, 0, 0, 1, 'no'],[1, 1, 1, 1, 'yes'],[1, 0, 1, 2, 'yes'],[1, 0, 1, 2, 'yes'],[2, 0, 1, 2, 'yes'],[2, 0, 1, 1, 'yes'],[2, 1, 0, 1, 'yes'],[2, 1, 0, 2, 'yes'],[2, 0, 0, 0, 'no']]# 分类属性labels = ['年龄', '有工作', '有自己的房子', '信贷情况']print(dataSet)print()print(calcShannonEnt(dataSet))print()featLabels = []myTree = creat_tree(dataSet, labels, featLabels)print(myTree)print(get_tree_depth(myTree))print(get_num_leaves(myTree))#测试数据testVec = [0, 1, 1, 1]result = classify(myTree, featLabels, testVec)if result == 'yes':print('放贷')if result == 'no':print('不放贷')# 存储树storeTree(myTree,'classifierStorage.txt')# 读取树myTree2 = grabTree('classifierStorage.txt')print(myTree2)testVec2 = [1, 0]result2 = classify(myTree2, featLabels, testVec)if result2 == 'yes':print('放贷')if result2 == 'no':print('不放贷')

9、运行结果

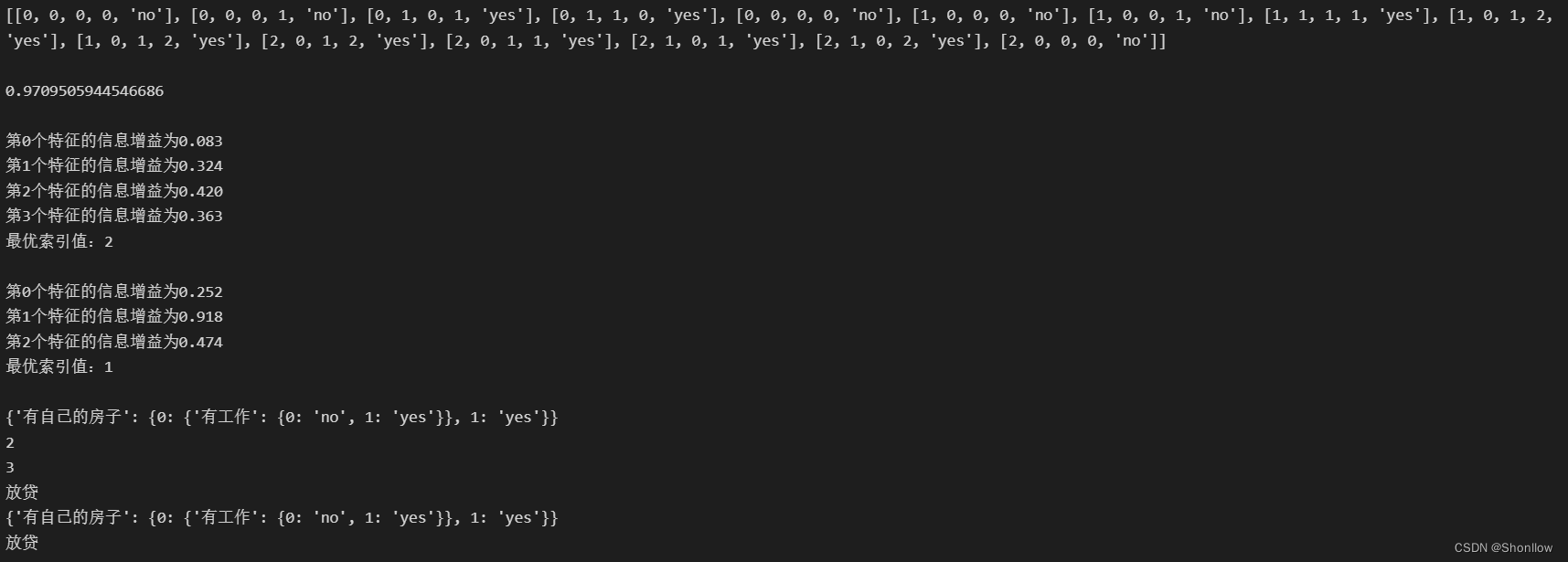
 通过我们的运行结果我们可知计算得出的香农熵为0.97。

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！