文章目录

• 典型例题一：石子合并
• • 1.1 题目：
  • 1.2 分析：
  • 1.3 完整代码：
• 典型例题二：环形石子合并
• • 2.1 题目：
  • 2.2 分析：
  • 2.3 完整代码:

顾名思义：区间dp就是在区间上进行动态规划，求解一段区间上的最优解。主要是通过合并小区间的 最优解进而得出整个大区间上最优解的dp算法。

典型例题一：石子合并

1.1 题目：

题目链接

1.2 分析：

1.2.1 状态表示：
f[l,r]表示把从L到R合并成一堆的最小代价。
1.2.2 状态转移：

1. 先把区间[L,R]切分成两部分[L,K], [K+1，R], k是切分点；
2. 再把两部分[L,R]和[k+1，R]合并在一起。（利用前缀和求区间和）

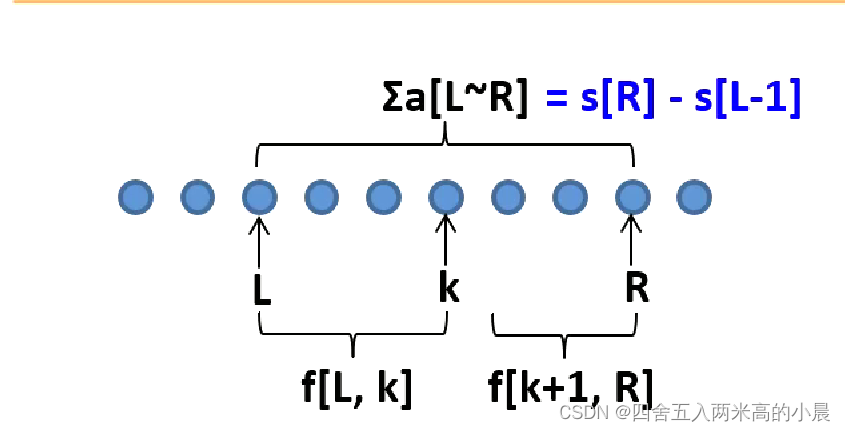
转移：
f[L,k] + f[k+1,R] + s[R] - s[L-1] ——>f[L,R]
计算：
f[L,R]=min(f[L,R] , f[L,k] + f[k+1,R] + s[R] - s[L-1])

1.2.3 边界情况：
f[i,i]=0(合并每堆石子的代价为0），其余为正无穷。

1.3 完整代码：

// 算法：区间DP
// 时间：2022.07.13 20点06分
#include
#include
using namespace std;const int N=310;
int n;//石子堆数
int s[N];//记录前缀和 用来求合并时候花费的代价
int f[N][N];//f[i][j]表示把从l到r合并成一堆的最小代价
int main ()
{cin>>n;for(int i=1;i<=n;i++) cin>>s[i];//求前缀和for(int i=1;i<=n;i++) s[i]+=s[i-1];for(int len=2;len<=n;len++)//阶段：枚举区间长度for(int i=1;i+len-1<=n;i++)//状态：枚举区间起点{int l=i,r=i+len-1;//区间的左右端点f[l][r]=1e9;for(int k=l;k<r;k++)//决策：枚举分割点//枚举最后一次合并的分界点f[l][r]=min(f[l][r],f[l][k]+f[k+1][r]+s[r]-s[l-1]);}cout<<f[1][n]<<endl;return 0;}

典型例题二：环形石子合并

2.1 题目：

2.2 分析：

这个问题只是将例题一的链式石子合并转换为环形，那么我们首先可以想到将环形问题转换为链式。对于环上的每一条边进行切割将其变为链式，所以只需要再多加一层循环即可。

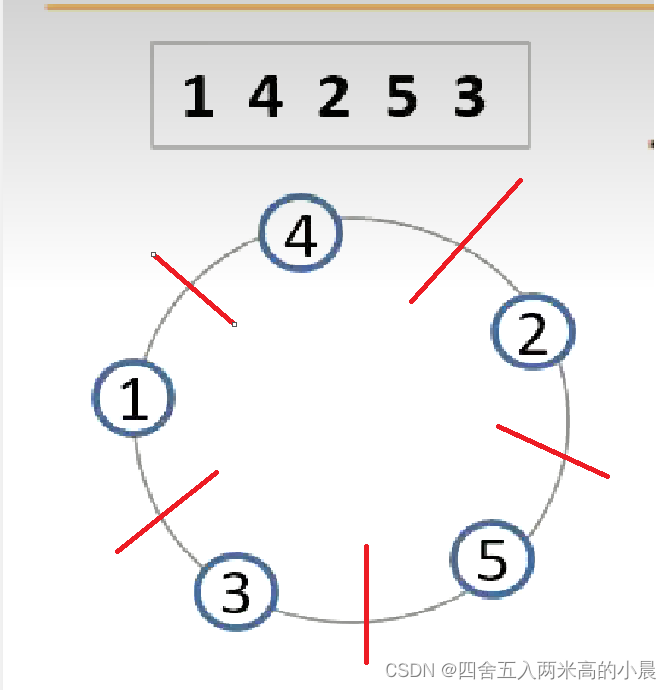
核心代码：

for(int j=1;j<=n;j++)//枚举环形的缺口for(int len=2;len<=n;len++)//阶段：枚举区间长度for(int i=1;i+len-1<=n;i++)//状态：枚举区间起点{int l=i,r=i+len-1;//区间的左右端点f[l][r]=1e9;for(int k=l;k<r;k++)//决策：枚举分割点//枚举最后一次合并的分界点f[l][r]=min(f[l][r],f[l][k]+f[k+1][r]+s[r]-s[l-1]);}

但是显而易见时间复杂度是O（n⁴)，所以会TLE,那么如何进行优化呢？？
这里提供一种常见的环形问题转换为链式的一种方法：
复制一遍数组，转化为长度为2N的链形数组。

核心代码：

//链形石子合并模板
for(int len=2;len<=n;len++)//阶段：枚举区间长度for(int l=1;l+len-1<=2*n;l++){//状态：枚举区间起点int r=l+len-1;//区间终点for(int k=l;k<r;k++)//决策：枚举分割点f[l][r]=min(f[l][r],f[l][k]+f[k+1][r]+s[r]-s[l-1]);}

2.3 完整代码:

#include
using namespace std;const int N=110,INF=0x3f3f3f3f;
int n;
int a[N];
int s[N];//记录前缀和
int f[N][N];//f[l][r]表示把从l到r合并成一堆的得分的最小值
int g[N][N];//g[l][r]表示把从l到r合并成一堆的得分的最大值
int main ()
{memset(f,INF,sizeof f);memset(g,-INF,sizeof g);cin>>n;for(int i=1;i<=n;i++){cin>>a[i];a[i+n]=a[i];//复制一遍区间}for(int i=1;i<=2*n;i++){s[i]=s[i-1]+a[i];//前缀和g[i][i]=0,f[i][i]=0;}//DPfor(int len=2;len<=n;len++)for(int l=1;l+len-1<=2*n;l++){int r=l+len-1;for(int k=l;k<r;k++){f[l][r]=min(f[l][r],f[l][k]+f[k+1][r]+s[r]-s[l-1]);g[l][r]=max(g[l][r],g[l][k]+g[k+1][r]+s[r]-s[l-1]);}}//输出int minv=INF,maxv=-INF;for(int i=1;i<=n;i++){minv=min(minv,f[i][i+n-1]);maxv=max(maxv,g[i][i+n-1]);}cout<<minv<<endl<<maxv<<endl;return 0;
}

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！