机器学习中矩阵向量求导
以下内容是根据刘建平的求导博客做的相关笔记
一、导数的定义与布局
1. 相关说明

2.导数布局
导数部分有分子布局和分母布局两种情况。
分子布局和分母布局相差一个转置。
- 标量对向量求导布局

- 向量对向量求导布局

- 求导布局总结
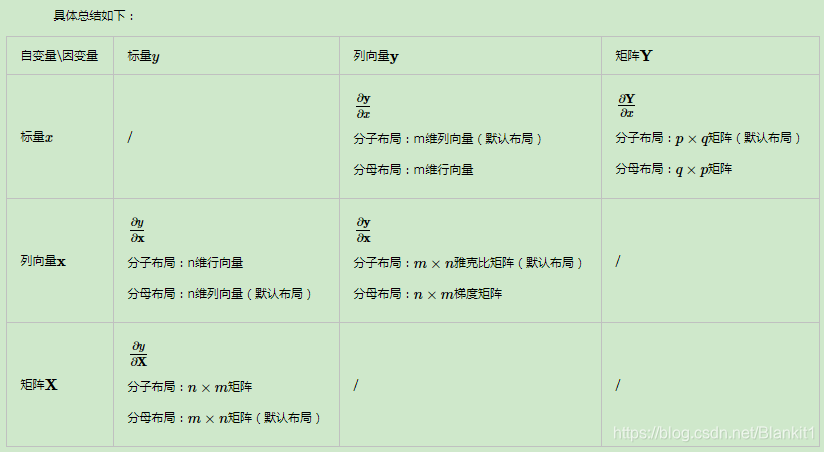
- 标量对向量或矩阵求导,以分母布局为主。向量对向量求导,以分母布局为主。
二、矩阵向量求导之定义法
写出单个元素间的求导关系,得出求导结果。
思路简单,适用于求解简单关系的导数
2.1 标量对向量求导


2.2 标量对矩阵求导

2.3 向量对向量求导

三、矩阵向量求导之微分法
3.1 矩阵微分

3.2 矩阵微分的性质
矩阵迹相关

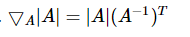
A∗A∗=∣A∣A*A^{*}=\left|A\right|A∗A∗=∣A∣
A∗=∣A∣A−1A^{*}=\left|A\right|A^{-1}A∗=∣A∣A−1
A∗A^{*}A∗是AAA的伴随矩阵,AAA相应位置的代数余子式构成的矩阵
3.3使用微分法求解矩阵向量求导

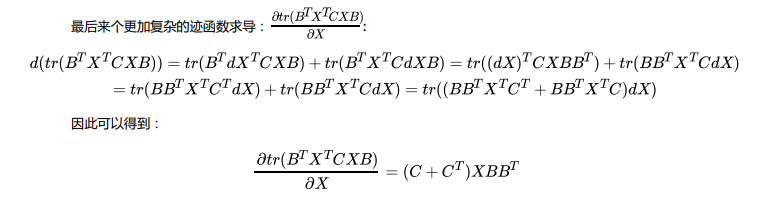
d(tr(X))=tr(d(x))d(tr(X))=tr(d(x))d(tr(X))=tr(d(x))
(uv)′=u′v+uv′(uv)^{'}=u^{'}v+uv^{'}(uv)′=u′v+uv′
四、链式法则
4.1 链式法则与矩阵相容
链式关系成立的条件是,相互关联的变量都是向量。

x\bm{x}x,y\bm{y}y,z\bm{z}z都是向量时,用上面的链式法则公式直接求解。
当最终的变量是标量时,按上面公式计算会出现维度不相容的情况。需要按下面的方法计算:

本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!