120. 三角形最小路径和

给定一个三角形，找出自顶向下的最小路径和。每一步只能移动到下一行中相邻的结点上。

相邻的结点 在这里指的是 下标 与 上一层结点下标 相同或者等于 上一层结点下标 + 1 的两个结点。

例如，给定三角形：

[
[2],
[3,4],
[6,5,7],
[4,1,8,3]
]
自顶向下的最小路径和为 11（即，2 + 3 + 5 + 1 = 11）。

说明：

如果你可以只使用 O(n) 的额外空间（n 为三角形的总行数）来解决这个问题，那么你的算法会很加分。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/triangle
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

三角形如下图

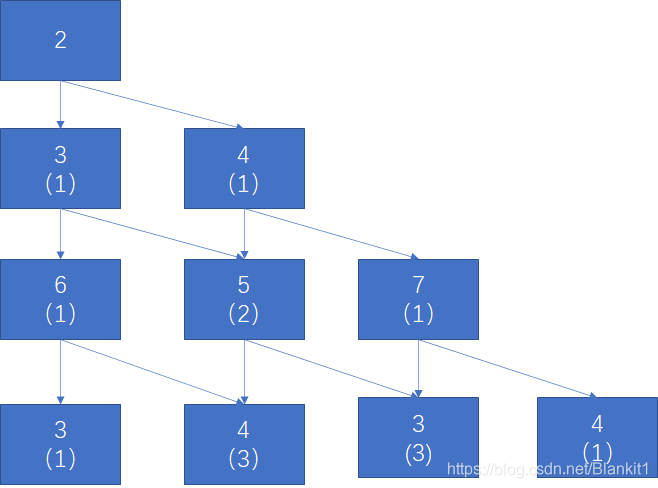
1 自顶向下方法

分析
加入一个棋子一开始在最顶层，他只能走向下一个或者斜下方的那格，每个格子都有权重，找出从最顶层向下走到最底层的最小权重和的路径。

括号内表示从顶层走到这个格子，有几条路径

1. 1二维矩阵的方法

构建一个相同的三角形S，S的第一个元素与给定矩阵的相同。
下面一个元素可以通过上面两条路径走下来，它的正上方的和左上方的。比如第三行的元素5（坐标(2，1)），可以从元素3（坐标（ 1，0 ））或者4 （坐标（ 1，1））走过来。如果保证，每次走下来的路径是上一层中，路径较小的那一条，那么到最后一层的时候，就是最小权重和的路径。在S中元素记录的是从顶层走到该处最小的路径权重。$S[i][j]=triangle[i][j]+min(s[i-1][j],s[i-1][j-1])$
还需要考虑边界条件:

• 最左边的元素，只能从正上方的元素哪里走下来
  $S[i][0]=triangle[i][0]+s[i-1][0]$
• 最右方的元素，只能从斜上方的元素走过来
  $S[i][i]=triangle[i][i]+s[i-1][i-1]$

构建完S矩阵后，返回最后一行最小的元素即可

class Solution:def minimumTotal(self, triangle) -> int:# triangle = [[2], [3, 4], [6, 5, 7], [4, 1, 8, 3]]# triangle = [[-1],[3,2],[1,-2,-1]]s = triangle.copy()# print(triangle)# print(s)l = len(triangle)if l < 1:returnelif l == 1:return s[0][0]else:s[0][0] = triangle[0][0]# s[1][0] = s[0][0] + triangle[1][0]# s[1][1] = s[0][0] + triangle[1][1]# print('after 1 epoch', s)for i in range(1, l):for j in range(i):if j == 0:s[i][0] = triangle[i][0] + s[i - 1][0]else:s[i][j] = triangle[i][j] + min(s[i - 1][j], s[i - 1][j - 1])s[i][i] = triangle[i][i] + s[i - 1][i - 1]# print(s)return min(s[l-1])

1.2一维数组

二维数组方法求解时，最重要的一步是
$S[i][j]=triangle[i][j]+min(s[i-1][j],s[i-1][j-1])$
可以看上，下一行的路径和只与上一层有关系，与上上层、上上上层…没有关系。所以可以构建一个以为数组，保存上一层路径的结果。另外新建一个以为数组，保存该层的结果就可以了。

class Solution:def minimumTotal(self, triangle):# triangle = [[2], [3, 4], [6, 5, 7], [4, 1, 8, 3]]# triangle = [[-1],[3,2],[1,-2,-1]]# s = triangle.copy()# print(triangle)# print(s)l = len(triangle)if l < 1:returnelif l == 1:return triangle[0][0]else:s = triangle[0]# s[1][0] = s[0][0] + triangle[1][0]# s[1][1] = s[0][0] + triangle[1][1]# print('after 1 epoch', s)for i in range(1, l):r = []for j in range(i):if j == 0:temp = triangle[i][j] + s[j]else:temp = triangle[i][j] + min(s[j], s[j - 1])r.append(temp)temp = triangle[i][i] + s[i - 1]r.append(temp)s = r.copy()# print(s)return min(s)

2 自下而上

从最后一层开始往上走，在原矩阵上就地操作，每个位置保存从下向上的最短路径$$triangle[i][j]=triangle[i][j]+min(triangle[i+1][j],triangle[i+1][j+1])$$

class Solution:def minimumTotal(self, triangle):l = len(triangle)for i in range(l-2,-1,-1):for j in range(i+1):triangle[i][j] = triangle[i][j]+min(triangle[i+1][j],triangle[i+1][j+1])return triangle[0][0]

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！