二叉树的深度和高度

二叉树的深度和高度的定义是不一样的，并且是相反的。深度是从上往下数的，高度是从下往上数的，即深度是从根节点到该节点的距离，高度是该节点到叶子节点的距离。当然树的高度和深度是相等的。

根节点的深度和高度为0，所以如果根节点的左右孩子不为空的话，那么根节点的左右孩子的深度就为1(并不是2）。

由于树的深度是从上往下，所以需要先遍历中间节点，所以遍历顺序为中左右，即前向遍历；树的高度是从下往上，所以需要先遍历孩子节点，所以遍历顺序是左右中，即后向遍历。

求节点的高度的方法：

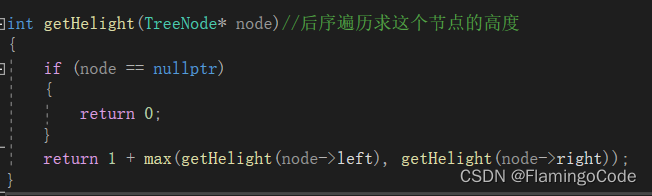
例题分析：

1、求树的最大深度。

二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。

 树的高度就是最大深度，所以求树的最大深度可以通过求根节点的高度来进行求解。

代码如下：

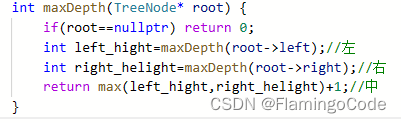
 2、求树的最小深度

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

叶子节点：左右孩子都为空的节点。

遍历顺序也是后向遍历。左右中。

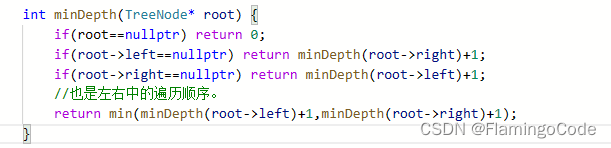
如果一个节点的左孩子为空且右孩子不为空，那么这个节点不为叶子节点，所以应该继续从右孩子继续往下计数，直到一个节点的左右孩子都为空才停止。

所以左孩子为空，应该继续去研究右孩子；右孩子为空，应该继续去研究左孩子。全为空，就停止计数。

代码如下：

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！