文章目录

• 一、巴什博弈(Bash Game)
• • 引例，最古老的一个游戏：
  • • 分析
    • 归纳
  • 巴什博弈(一般化)
  • • 问题描述
    • 代码示例
• 二、威佐夫博弈(Wythoff Game)
• • 问题描述
  • 解题结论
  • 代码示例
• 三、尼姆博弈 (Nimm Game)
• • 问题描述
  • 解题结论
  • 代码示例
• 四、斐波那契博弈
• • 问题描述
  • 解题结论
  • 代码示例
• 总结

借鉴了大佬的资料：
博弈论.

一、巴什博弈(Bash Game)

引例，最古老的一个游戏：

A和B一块报数，每人每次报最少1个，最多报4个，看谁先报到30(第30个数)。

分析

第一次报数，A报出数的个数是 x ，那么 B报数 5-x 个，接着现在问题变成了下面这个样子：
A 和 B 一块报数，看谁先报到第25个
然后问题逐渐简化，规模缩小：20、15、10、5。最后问题是看谁先报到 5，这时无论 A 怎么报数，最后一个数一定是 B 报出来的，所以 B 必胜。从这里的分析可以得到：
作为后手的 B 在这次游戏中是不会输的。

归纳

如果我们要报 n 个数，每次最少报 1 个，最多报 m 个，可以找出这么一个整数 k 和 r ，使得 n = k * (m+1) + r，代入引例中可知，如果 r = 0 ，那么先手必败，否则，先手必胜（这里我还不太会证明。。。）。

巴什博弈(一般化)

问题描述

只有一堆 n 个物品，两个人轮流从中取物，规定每次最少取 1 个，最多取 m 个，最后取光者为胜

代码示例

#include
using namespace std;
int main()
{int n, m;while (cin >> n >> m){if (n % (m + 1) == 0){cout << "后手必胜" << endl;//先手必败}else{cout << "先手必胜" << endl;}}return 0;
}

二、威佐夫博弈(Wythoff Game)

问题描述

有两堆各若干的物品，两人轮流从其中一堆取至少 1 件物品，至多不限，或从两堆中同时取相同件物品，规定最后取完者胜利。

解题结论

若两堆物品数量的初始值是 (x, y)，且 x < y，则令 z = y - x；
设 *w=（int）[（（sqrt（5）+1）/2）z ]；
(下图是人话)

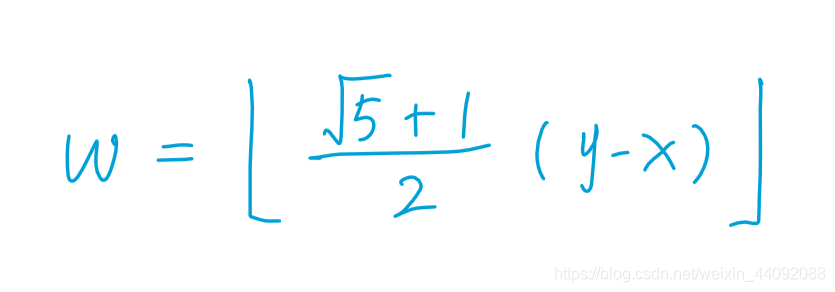
若 w = x，先手必败，否则后手必败；

代码示例

#include
#include
using namespace std;int main()
{int n1, n2, temp;while (cin >> n1 >> n2){if (n1 > n2) //保证 n1 <= n2{swap(n1, n2);}temp = floor((n2 - n1) * (sqrt(5.0) + 1) / 2.0);if (temp == n1){cout << "后手必胜" << endl;}else{cout << "先手必胜" << endl;}}return 0;
}

三、尼姆博弈 (Nimm Game)

问题描述

有任意堆物品，每堆物品的个数是任意的，两个人轮流从中取物品，每一次只能从一堆物品中取部分或全部物品，最少取 1 件，取到最后一件物品的人获胜。

解题结论

把每堆物品数全部异或起来，如果得到的值为 0 ，那么先手必败(后手必胜)，否则先手必胜。

代码示例

#include
#include
using namespace std;
int main()
{int i, n, ans, temp;// n 堆物品while (cin >> n){temp = 0;for ( i = 1; i <= n; i++){cin >> ans;temp ^= ans; //我们把每一堆的物品数给异或起来}if (temp == 0){cout << "后手必胜" << endl;}else{cout << "先手必胜" << endl;}}return 0;
}

四、斐波那契博弈

问题描述

有一堆物品，两人轮流取物品，先手最少取一个，至多无上限，但是不能把物品取完，之后每次取得物品数不能超过上一次取的物品数的 2 倍且至少为 1 件，取走最后 1 件物品的人获胜。

解题结论

当且仅当 n 是斐波那契数(n 为物品总数)时，先手必败。

代码示例

#include
#include
using namespace std;
#define N 55
int f[N] = {}; //斐波那契数列void Init();int main()
{bool flag = false; // true : 先手必败，flase : 后手必败int n, i;Init();while (cin >> n){if (n == 0)//不用玩了{break;}flag = false;for ( i = 0; i < N; i++) //判断是否是斐波那契数，只好一个一个试{if (n == f[i]){flag = true;//先手必败break;}}if (flag){cout << "后手必胜" << endl;}else{cout << "先手必胜" << endl;}}return 0;
}void Init()
{int i;f[0] = 1;f[1] = 1;for ( i = 2; i < N; i++){f[i] = f[i - 1] + f[i - 2];}
}

总结

可以注意到以上所有博弈问题
1、获胜条件都是取到最后一件物品；
2、如果结果满足对应条件，先手必败；

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！