开啃《机器学习》（周志华）- 第2章 模型评估与选择

重要概念：

• 错误率（error rate）：分类错误的样本占样本总数的比例
• 精度（accuracy）：分类正确的样本占样本总数的比例，精度=1-错误率
• 训练误差（training error）：学习器的实际预测输出与训练样本真实输出之间的差异
• 泛化误差（generalization error）：学习器的实际预测输出与新样本真实输出之间的差异
• 过拟合（overfitting）：把训练样本自身的一些特点，当作潜在样本的一般性质，常常表现为-训练输出精度很高但泛化输出精度不高
• 欠拟合（underfitting）：对训练样本的一般特性学习不够，影响了泛化性能，表现为-训练输出和泛化输出精度都不高
• 参数调节（parameter tuning）：包括算法参数和模型参数的调整；调参出来的值往往非最佳值，因为无法遍历参数的所有取值，但适当调参对模型性能的更优选择有积极意义。

学习模型的目标：

      通过一系列手段，获得泛化误差最小的学习器

评估方法（如何利用已有样本构造训练和测试样本，并获取泛化误差的近似值）：

    1. hold-out：将样本数据分为训练集和测试集，训练集用于训练，测试集用于评估泛化误差

• 训练和测试集的划分要尽可能保持数据分布的一致性
• 一般采用若干次随机划分，重复实验后算出平均值作为泛化精度指标
• 一般，训练集占比2/3~4/5

    2. cross-validation：将数据集D划分为k个大小相似的互斥子集，每次取其中一个子集作为测试集，剩余的并集作为训练集，则共训练k次

• k个子集的划分一般也采用若干次（假设为p次）随机划分，然后得到所有的测试结果求均值，训练总次数为k*p
• Leave-One-Out：假设数据集大小为m，且m=k，为cross-validation的特例，评估结果比较准确（因为每次训练集为m-1个，训练特性与数据集整体特性非常接近），但不适用于数据集比较大的情况

    3. bootstrapping：对数据集D随机采样m次（m为D的大小）放到新的数据集D1中，将D1作为训练集，D\D1（即D减掉D1后剩余的数据集）作为测试集

• 训练集样本总数等于数据集样本总数，但训练集样本有重复样本，不重复样本占原数据集比例约为（1-1/e）=63.2%，测试集样本占原数据集比例约为1/e=36.8%
• 解决训练样本规模与数据集规模不一致的问题，减少一定估计偏差；但训练样本更改了数据集分布，会引入其他估计偏差
• 在初始数据量够的情况下，建议优先考虑cross-validation和hold-out

 性能度量：

    另：参考机器学习性能评估指标

    1. error rate（错误率）与accuracy（精度）：

• 离散数据集情况：

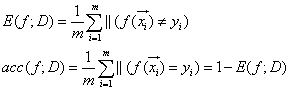
          其中，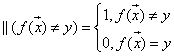

• 连续数据集情况：

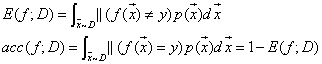
         其中，p()为样本的概率密度函数

    2. precision（查准率）与recall（查全率/召回率）：

• TP（true positive）：预测等于真实，且预测为正例
• FP（false positive）：预测不等于真实，且预测为正例（误报）
• TN（true negative）：预测等于真实，且预测为反例
• FN（false negative）：预测不等于真实，且预测为反例（漏报）
• precision = TP / (TP+FP)：预测为正例的情况中，预测准确的比例（挑出来的所有西瓜，好瓜所占的比例）- 衡量正例预测准确率的指标
• recall = TP / (TP+FN)：真实为正例的样本中，被挑出来的比例（所有好瓜当中，能被挑出来的比例）- 表示找到所有正例的能力
• Break-Event Point（查准/召回 平衡点）：PR曲线中precision=recall的点，每次测试得到的PR曲线，平衡点对应的P值或R值越大，则学习器的性能越好
• F1 = 2*P*R/(P+R)：基于precision和recal的harmonic mean（调和平均，1/F1=0.5*(1/P+1/R)）

    3. ROC与AUC

      理解参考：http://www.cnblogs.com/dlml/p/4403482.html

• TPR（true positive rate）= TP / (TP+FN)：真实为正例的样本中，被挑出来当成正例的比例，值同recall
• FPR（false positive rate）= FP / (FP+TN)：真实为反例的样本中，被挑出来当成正例的比例（所有坏瓜当中，被挑出来当成好瓜的比例）
• ROC（Receiver Operation Charateristics）曲线：横轴为FPR，纵轴为TPR，用于评价分类器的好坏
• ??? AUC（Area Under ROC Curve）：ROC曲线面积，表征分类器在不同阀值预测下，TPR大于FPR的概率；0.5

    4. cost-sensitive error rate & cost curve：权衡不同类型错误所造成的不同损失，当不同错误存在“非均等代价”（unequal cost）时使用

• cost matrix（代价矩阵）：第i行第j列的值cost(i,j)，代表在样本预测时，将第i类判别为第j类所造成的损失；当i=j时为正确判断，因此cost(i,i)=0；对于二分类器，cost matrix大小为2*2
• cost-sensitive error rate（代价敏感错误率）：在error rate的基础上，乘上对应的代价，得到total cost（总体代价）；最小化total cost作为学习器调整和优化的目标
• FNR（false negative rate）= FN/ (FN+TP)=1-TPR：真实为正例的样本中，未被挑出来的比例；与FPR一起，对应2维cost matrix中两个非0代价产生的概率值
• cost curve graph（代价曲线图，以二分类器为例）：

          横轴为，p是样本为正例的概率，P(+)称为正例概率代价

          纵轴为，为归一化代价

• 获取cost curve & total cost：ROC曲线每一对(FPR, TPR)值，换算出(0,FPR)和(1,FNR)，构成从(0,FPR)到(1,FNR)的多条交叉的线段，取各个线段的下界围成的区域的面积为total cost，围成区域的折线即为cost curve

比较检验（如何选择适当的方法对学习器的性能指标进行比较）：

    1. hypothesis test（假设检验，为性能比较提供重要依据；对单个学习器泛化性能的假设进行检验）

• binomial test（二项检验）
• t-test（t检验）

    2. 交叉验证t检验

       ......未理解的部分（待补充）

偏差与方差

    1. 泛化误差可分解为Bias（偏差），Variance（方差）与噪声之和

    2. 偏差与方差的区别：

• Bias：预测值（估计值）的数学期望与真实值之间的差距；偏差越大，越偏离真实数据
• Variance：预测值的变化范围，离散程度，也就是离其期望值的距离；方差越大，数据的分布越分散

转载于:https://www.cnblogs.com/wrightcw/p/7885548.html

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！