如下图的九宫格中，放着 1 ~ 8 的数字卡片，还有一个格子空着。与空格子相邻的格子中的卡片可以移动到空格中。 经过若干次移动，可以形成图 2 所示的局面。

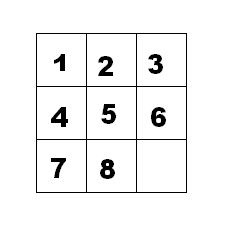
我们把上图的局面记为：12345678.

把下图的局面记为：123.46758

显然是按从上到下，从左到右的顺序记录数字，空格记为句点。

题目的任务是已知九宫的初态和终态，求最少经过多少步的移动可以到达。如果无论多少步都无法到达，则输出 -1。

输入描述

输入第一行包含九宫的初态，第二行包含九宫的终态。

输出描述

输出最少的步数，如果不存在方案，则输出 -1。

输入输出样例

示例

输入

12345678.
123.46758

输出

3

典型的BFS问题，像这一种在一个平面上移动的，要先移动空的格子，这样就可以只移动一个格子就行，如果是移动数字的话就要移动八个数。可以先把一维数转换成为二维数组的下标来进行移动，移动完后再把其转换成一维数组

具体转换公式:

一维转二维 ： x = index // 数组宽度 ， y = index % 数组宽度

二维转一维 ： x * 3 + y

代码实现 

import collections
def bfs():q = collections.deque()dist = {}                                           #使用字典存储步数dist[s1] = 0dire = [(1,0),(-1,0),(0,1),(0,-1)]q.append(s1)while q:now = list(q.popleft())                         #将pop出来的字符串逐个加入列表，方便操作if "".join(now) == s2:return dist["".join(now)]                   #如果达到要求，返回次数point = now.index(".")                          #找到移动“.”的索引x = point // 3                                  #一维转二维下标，可以自己举个例子试一下y = point % 3distance = dist["".join(now)]for i in dire:tx,ty = inx,ny = x + tx, y + tyif nx in [0,1,2] and ny in [0,1,2]:         #如果没有过界new_now = now.copy()new_now[point],new_now[nx*3 + ny] = new_now[nx*3 + ny],new_now[point]       #二维转一维if "".join(new_now) not in dist.keys():                                     #如果没有出现过在字典中，就创建并且步数加1dist.setdefault("".join(new_now),distance+1)q.append("".join(new_now))return -1s1 = input()
s2 = input()
print(bfs())

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！