目录

一、剩余BPR算法的优化

二、算法流程

三、BPR算法的实现代码

 四、性能指标的补充

五、参考文献

一、剩余BPR算法的优化

上次化简到该步

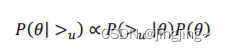
 对于第一部分，由于我们假设每个用户之间的偏好行为相互独立，同一用户对不同物品 的偏序相互独立，所以有：

其中：

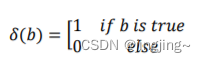
 根据上面讲到的完整性和反对称性，优化目标的第一部分可以简化为：

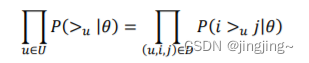
而对于𝑃(𝑖 >𝑢 𝑗|𝜃)这个概率，我们可以使用下面这个式子来代替:

𝜎(𝑥)是 sigmoid 函数，满足这三个性质且方便优化计算。

对于𝑥𝑢𝑖𝑗(𝜃)这个式子，我们要满足当𝑖 >𝑢 𝑗时，𝑥𝑢𝑖𝑗(𝜃) > 0, 反之当𝑗 >𝑢 𝑖时，𝑥𝑢𝑖𝑗(𝜃) < 0，最简单的表示这个性质的方法就是：

而𝑥𝑢𝑖(𝜃), 𝑥𝑢𝑗(𝜃)，就是我们的矩阵𝑋对应位置的值。这里为了方便，我们不写𝜃,这样上 式可以表示为:

注意上面的这个式子也不是唯一的，只要可以满足上面提到的当𝑖 >𝑢j 时，𝑥𝑢𝑖𝑗(𝜃) > 0， 以及对应的相反条件即可。最终，我们的第一部分优化目标转化为： 

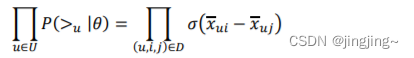
对于第二部分𝑃(𝜃)，使用了贝叶斯假设，即这个概率分布符合正太分布，且对应的均值是 0，协方差矩阵是𝜆𝜃I,即 

为了优化方便，因为后面做优化时，需要计算𝑙𝑛𝑃(𝜃)，而对于上面假设的这个多维正态分布，其对数和||𝜃|| 2成正比。即： 

最终对于我们的最大对数后验估计函数(即BPR损失函数):

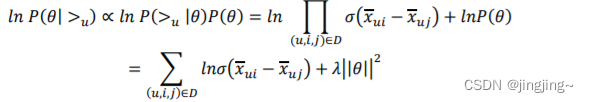
这个式子可以用梯度上升法或者牛顿法等方法来优化解，解模型参数。

如果用梯度上升 法，对𝜃解导有： 

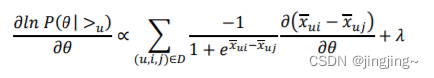
由于，

所有可以求得，

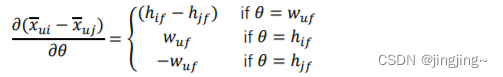
这样就有了梯度迭代式子。再用梯度上升法解解模型参数。 

二、算法流程

输入：训练集D三元组，梯度步长α，正则化参数λ,分解矩阵维度k。　　　　　　　　　　
输出：模型参数，矩阵W,H
　　1. 随机初始化矩阵W,H
　　2. 迭代更新模型参数

       3. 如果W,H收敛，则算法结束，输出W,H，否则回到步骤2.
　　 当我们拿到W,H后，就可以计算出每一个用户u对应的任意一个商品的排序分，最终选择排序分最高的若干商品输出。

三、BPR算法的实现代码

第一部分的代码，文件命名为BPR_basical.py

import random
from collections import defaultdict
import numpy as np
from sklearn.metrics import roc_auc_score
import scoresclass BPR:user_count = 943item_count = 1682latent_factors = 20lr = 0.01reg = 0.01train_count = 1000train_data_path = 'train.txt'test_data_path = 'test.txt'size_u_i = user_count * item_count# latent_factors of U & VU = np.random.rand(user_count, latent_factors) * 0.01V = np.random.rand(item_count, latent_factors) * 0.01biasV = np.random.rand(item_count) * 0.01test_data = np.zeros((user_count, item_count))test = np.zeros(size_u_i)predict_ = np.zeros(size_u_i)def load_data(self, path):user_ratings = defaultdict(set)with open(path, 'r') as f:for line in f.readlines():u, i = line.split(" ")u = int(u)i = int(i)user_ratings[u].add(i)return user_ratingsdef load_test_data(self, path):file = open(path, 'r')for line in file:line = line.split(' ')user = int(line[0])item = int(line[1])self.test_data[user - 1][item - 1] = 1def train(self, user_ratings_train):for user in range(self.user_count):# sample a useru = random.randint(1, self.user_count)if u not in user_ratings_train.keys():continue# sample a positive item from the observed itemsi = random.sample(user_ratings_train[u], 1)[0]# sample a negative item from the unobserved itemsj = random.randint(1, self.item_count)while j in user_ratings_train[u]:j = random.randint(1, self.item_count)u -= 1i -= 1j -= 1r_ui = np.dot(self.U[u], self.V[i].T) + self.biasV[i]r_uj = np.dot(self.U[u], self.V[j].T) + self.biasV[j]r_uij = r_ui - r_ujloss_func = -1.0 / (1 + np.exp(r_uij))# update U and Vself.U[u] += -self.lr * (loss_func * (self.V[i] - self.V[j]) + self.reg * self.U[u])self.V[i] += -self.lr * (loss_func * self.U[u] + self.reg * self.V[i])self.V[j] += -self.lr * (loss_func * (-self.U[u]) + self.reg * self.V[j])# update biasVself.biasV[i] += -self.lr * (loss_func + self.reg * self.biasV[i])self.biasV[j] += -self.lr * (-loss_func + self.reg * self.biasV[j])def predict(self, user, item):predict = np.mat(user) * np.mat(item.T)return predictdef main(self):user_ratings_train = self.load_data(self.train_data_path)self.load_test_data(self.test_data_path)for u in range(self.user_count):for item in range(self.item_count):if int(self.test_data[u][item]) == 1:self.test[u * self.item_count + item] = 1else:self.test[u * self.item_count + item] = 0# trainingfor i in range(self.train_count):self.train(user_ratings_train)predict_matrix = self.predict(self.U, self.V)# predictionself.predict_ = predict_matrix.getA().reshape(-1)self.predict_ = pre_handel(user_ratings_train, self.predict_, self.item_count)auc_score = roc_auc_score(self.test, self.predict_)print('AUC:', auc_score)# Top-K evaluationscores.topK_scores(self.test, self.predict_, 5, self.user_count, self.item_count)def pre_handel(set, predict, item_count):# Ensure the recommendation cannot be positive items in the training set.for u in set.keys():for j in set[u]:predict[(u - 1) * item_count + j - 1] = 0return predictif __name__ == '__main__':bpr = BPR()bpr.main()

第二部分自写scores， 命名为scores.py和BPR_basical.py处于同级。

import heapq
import numpy as np
import math
#计算项目top_K分数
def topK_scores(test, predict, topk, user_count, item_count):PrecisionSum = np.zeros(topk+1)RecallSum = np.zeros(topk+1)F1Sum = np.zeros(topk+1)NDCGSum = np.zeros(topk+1)OneCallSum = np.zeros(topk+1)DCGbest = np.zeros(topk+1)MRRSum = 0MAPSum = 0total_test_data_count = 0for k in range(1, topk+1):DCGbest[k] = DCGbest[k - 1]DCGbest[k] += 1.0 / math.log(k + 1)for i in range(user_count):user_test = []user_predict = []test_data_size = 0for j in range(item_count):if test[i * item_count + j] == 1.0:test_data_size += 1user_test.append(test[i * item_count + j])user_predict.append(predict[i * item_count + j])if test_data_size == 0:continueelse:total_test_data_count += 1predict_max_num_index_list = map(user_predict.index, heapq.nlargest(topk, user_predict))predict_max_num_index_list = list(predict_max_num_index_list)hit_sum = 0DCG = np.zeros(topk + 1)DCGbest2 = np.zeros(topk + 1)for k in range(1, topk + 1):DCG[k] = DCG[k - 1]item_id = predict_max_num_index_list[k - 1]if user_test[item_id] == 1:hit_sum += 1DCG[k] += 1 / math.log(k + 1)# precision, recall, F1, 1-callprec = float(hit_sum / k)rec = float(hit_sum / test_data_size)f1 = 0.0if prec + rec > 0:f1 = 2 * prec * rec / (prec + rec)PrecisionSum[k] += float(prec)RecallSum[k] += float(rec)F1Sum[k] += float(f1)if test_data_size >= k:DCGbest2[k] = DCGbest[k]else:DCGbest2[k] = DCGbest2[k-1]NDCGSum[k] += DCG[k] / DCGbest2[k]if hit_sum > 0:OneCallSum[k] += 1else:OneCallSum[k] += 0# MRRp = 1for mrr_iter in predict_max_num_index_list:if user_test[mrr_iter] == 1:breakp += 1MRRSum += 1 / float(p)# MAPp = 1AP = 0.0hit_before = 0for mrr_iter in predict_max_num_index_list:if user_test[mrr_iter] == 1:AP += 1 / float(p) * (hit_before + 1)hit_before += 1p += 1MAPSum += AP / test_data_sizeprint('MAP:', MAPSum / total_test_data_count)print('MRR:', MRRSum / total_test_data_count)print('Prec@5:', PrecisionSum[4] / total_test_data_count)print('Rec@5:', RecallSum[4] / total_test_data_count)print('F1@5:', F1Sum[4] / total_test_data_count)print('NDCG@5:', NDCGSum[4] / total_test_data_count)print('1-call@5:', OneCallSum[4] / total_test_data_count)return

本次用到的训练集（train.txt）和测试集(test.txt)文件已上传资源中。

代码运行结果：

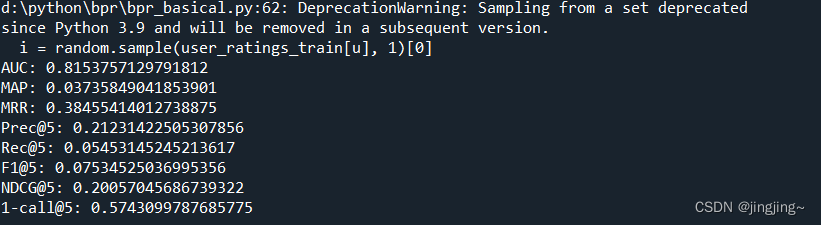
 四、性能指标的补充

MAP (Mean Average Precision)和MRR (Mean Reciprocal Rank) 是在信息检索领域中常用的评估指标。详细见（MRR,MAP等评估方法(常用与IR和QA任务) - 简书 (jianshu.com)）。

MAP (Mean Average Precision) 是用于评估信息检索系统排序质量的指标。在信息检索任务中，系统根据查询的相关性对文档进行排序，并返回前N个最相关的文档。MAP考虑了每个查询的平均精确性，它通过计算检索结果中每个相关文档的平均精确性来衡量系统的性能。MAP的值介于0和1之间，值越高表示系统的排名效果越好。

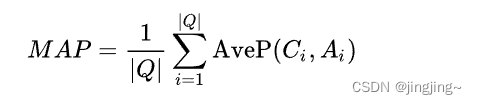
MRR (Mean Reciprocal Rank) 是用于评估信息检索系统的排序质量的指标之一。与MAP不同，MRR考虑的是排名第一个相关文档的位置。MRR的计算方式是取每个查询的倒数排名的平均值。在MRR中，相关文档的排名越高，得分越高，最佳结果为1。

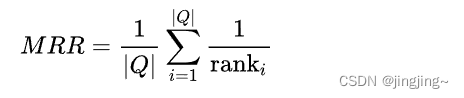
Precision、Recall、F1和1-call（或者称为False Negative Rate）是经常用来评估分类模型性能的指标。

Precision（精确率）衡量了模型预测为正例中有多少是真正的正例。它的计算公式是真正例（True Positives，TP）除以真正例加上假正例（False Positives，FP），即 Precision = TP / (TP + FP)。精确率越高，模型预测为正例的准确性越高。

Recall（召回率，也称为敏感度或真正例率）衡量了模型正确找出的正例占所有真正正例的比例。它的计算公式是真正例（TP）除以真正例加上假反例（False Negatives，FN），即 Recall = TP / (TP + FN)。召回率越高，模型找出真正正例的能力越强。

F1 Score（F1得分）是Precision和Recall的调和平均数，可以综合考虑模型的准确性和查全率。它的计算公式是2 * (Precision * Recall) / (Precision + Recall)。F1 Score的取值范围在0和1之间，值越高表示模型的性能越好。

1-Call（1-错误拒绝率）衡量了模型将负例（即真实为负例的样本）错误预测为正例的概率。它的计算公式是假正例（FP）除以真负例（True Negatives，TN）加上假反例（FN），即 1-Call = FP / (TN + FP)。1-Call越低，模型将负例错误预测为正例的能力越强。

这些指标都在分类模型的评估中起到重要的作用，通过比较它们的数值可以判断模型的准确性、查全率和错误拒绝率等性能。

NDCG（Normalized Discounted Cumulative Gain）是一种用于评估排序算法或推荐系统排序质量的指标。

在信息检索或推荐系统中，通常需要对一系列项目进行排序，并将最相关或最有用的项目排在前面。NDCG衡量了算法在排序中正确地放置相关项目的能力。

NDCG结合了两个重要的概念：折扣累计增益（DCG）和理想折扣累计增益（IDCG）。

DCG是通过对搜索结果进行打分和折扣加权之后的排序结果。具体计算方法是将每个项目的得分除以一个对数增益的折扣因子，再对项目进行累加。

IDCG是理想情况下的折扣累计增益，用于表示排序最优的情况。它通过将查询结果按照真实相关性得分进行排序，并计算出其折扣累计增益。

NDCG的计算方法是将DCG除以IDCG，再用1减去这个值，最后取平均值。它的取值范围在0和1之间，值越接近1表示排序质量越好。

五、参考文献

(1条消息) BPR贝叶斯个性化推荐算法—推荐系统基础算法（含python代码实现以及详细例子讲解）_bpr代码_啥都不懂的小程序猿的博客-CSDN博客

MRR,MAP等评估方法(常用与IR和QA任务) - 简书 (jianshu.com)

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！