电力电子技术(11)——变压器漏感对整流电路的影响、电容滤波
目录
2.3 变压器漏感对整流电路的影响
换相重叠角的计算
变压器漏抗对各种整流电路的影响
2.4 电容滤波的不可控整流电路
2.4.1 电容滤波的单相不可控整流电路
1)工作原理及波形分析
2)主要的数量关系
感容滤波的二极管整流电路
2.4.2 电容滤波的三相不可控整流电路
1)基本原理
2)主要数量关系
3)二极管承受的电压
2.3 变压器漏感对整流电路的影响
考虑包括变压器漏感在内的交流侧电感的影响,该漏感可用一个集中的电感表示。
以三相半波为例,然后将其结论推广。
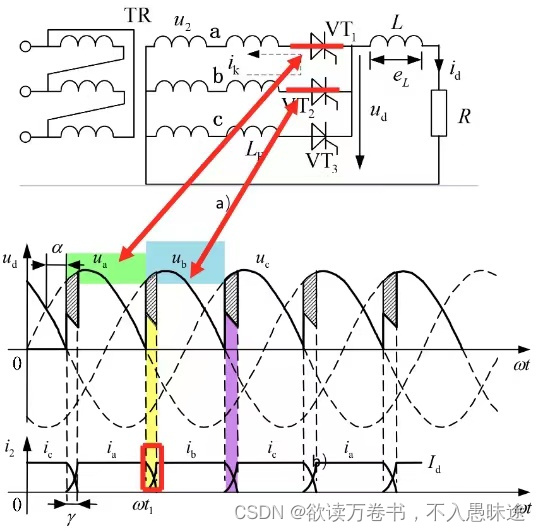
换相至
的过程:
因a、b两相均有漏感,故、
均不能突变。于是
和
同时导通,相当于将a、b两相短路,在两相组成的回路中产生环流
。
是逐渐增大的,而
是逐渐减小的。
当增大到等于
时,
,
关断,换流过程结束。
换相重叠角——换相过程持续的时间,用电角度表示。
换相过程中,整流电压为同时导通的两个晶闸管所对应的两个相电压的平均值。
换相压降——与不考虑变压器漏感时相比,平均值降低的多少。
换相重叠角的计算
由上式得:
进而得出:
当时,
,于是:
随其它参数变化的规律:
越大则
越大;
越大
越大;
- 当
时,
越小
越大。
变压器漏抗对各种整流电路的影响
| 电路形式 | 单相全波 | 单相全控桥 | 三相半波 | 三相全控桥 | m脉波整流电路 |
注意:
- 单相全控桥电路中,环流
是从
变为
。本表所列通用公式不适用;(对于单相桥式全控整流电路来说,在一周期的两次换相中都起作用,
用
代入。)
- 三相桥等效为相电压等于
的6脉波整流电路,故其m=6,相电压按
代入。单相全波m=2,三相半波m=3。
考虑漏抗造成换相压降后,输出整流电压平均值为:。
为时不考虑漏抗影响的整流电压平均值。
- 对于单相桥式可控整流电路感性负载:
。
- 对于三相半波可控整流电路 :
。
- 对于三相桥式可控整流电路:
。
正比于负载电流,相当于在整流电源增加了一项“内阻”,并不消耗功率。
变压器漏感对整流电路影响的一些结论:
- 出现换相重叠角
,整流输出电压平均值
降低。
- 整流电路的工作状态增多。(管子通断状态的组合由6种变为12种)
- 晶闸管的di/dt减小,有利于晶闸管的安全开通。有时人为串入进线电抗器以抑制晶闸管的di/dt。
- 换相时晶闸管电压出现缺口,产生正的du/dt,可能使晶闸管误导通,为此必须加吸收电路。
- 换相使电网电压出现缺口,成为干扰源。
2.4 电容滤波的不可控整流电路
在交——直——交变频器、不间断电源、开关电源等应用场合中,大量应用。
最常用的是单相桥和三相桥两种接法。
由于电路中的电力电子器件采用整流二极管(不可控),故也称这类电路为二极管整流电路。
2.4.1 电容滤波的单相不可控整流电路
常用于小功率单相交流输入的场合,如目前大量普及的微机、电视机等家用产品中。
1)工作原理及波形分析
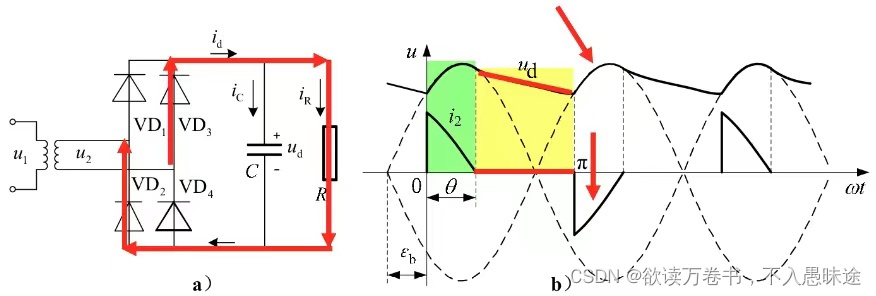
基本工作过程:
在正半周过零点至
期间,因
,故二极管均不导通,电容C向R放电,提供负载所需电流。
至之后,
将要超过
,使得
和
开通,
,交流电源向电容充电,同时向负载R供电。
2)主要的数量关系
输出电压平均值
空载时,。
重载时,逐渐趋近于
,即趋近于接近电阻负载时的特性。
在设计时根据负载的情况选择电容C值,使,此时输出电压为:
。
电流平均值
输出电流平均值为:
(电容电流平均值为0)。
二极管电流的平均值为:
。
二极管承受的电压:。
感容滤波的二极管整流电路
实际应用为此情况,但分析复杂。
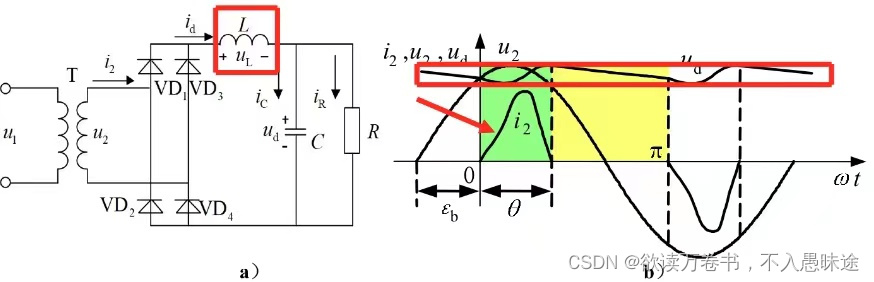
波形更平直,电流的上升段平缓了许多,这对于电路的工作是有利的。
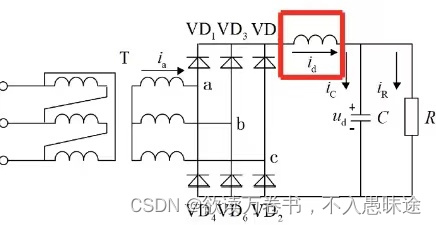
2.4.2 电容滤波的三相不可控整流电路
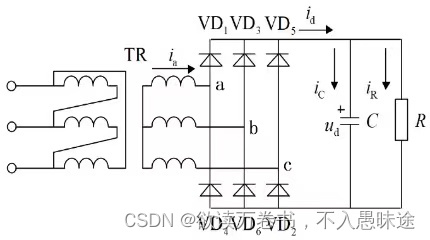
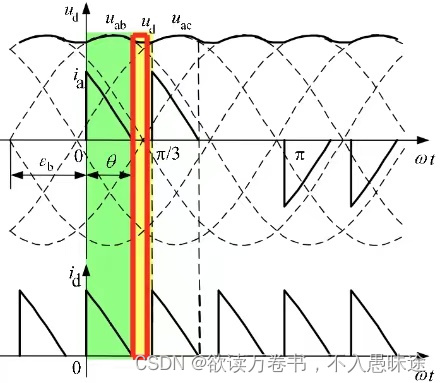
1)基本原理
某一对二极管导通时,输出电压等于交流侧线电压中最大的一个,该线电压既向电容供电,也向负载供电。
当没有二极管导通时,由电容向负载放电,按指数规律下降。
由“电压下降速度相等”的原则,可以确定临界条件。假设在的时刻“速度相等”恰好发生,则有
由上式可得,电流断续和连续的临界条件:
。
考虑实际电路中存在的交流侧电感以及抑制冲击电流而串联的电感时的工作情况:
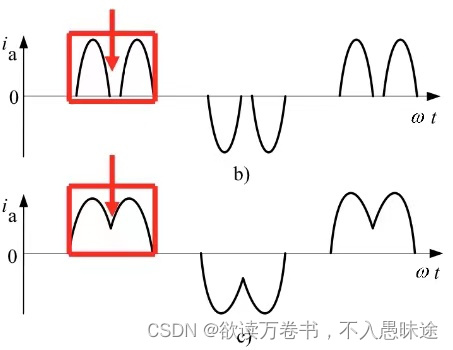
电流波形的前沿平缓了许多,有利于电路的正常工作。随着负载的加重,电流波形与电阻负载时的交流侧电流波形逐渐接近。
2)主要数量关系
输出电压平均值
在
之间变化。
电流平均值
输出电流平均值为:
。
与单相电路情况一样,电容电流的平均值为零,因此
。
二极管电流平均值为的1/3,即:。
3)二极管承受的电压
二极管承受的最大反向电压为线电压的峰值,为。
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!