C++ | 数据结构 | B树的讲解与模拟实现

文章目录

• • B树的性质
  • 搜索逻辑讲解
  • 插入逻辑讲解
  • B树的整体实现，文件展示

B树的性质

1.根节点至少有两个孩子
2.每个分支节点包含k-1个关键字和k个孩子，其中ceil(m/2) <= k <= m，ceil为向上取整，m是树的阶数
3.每个叶节点包含k-1个关键字，叶子节点就没有孩子了，其中ceil(m/2) <= k <= m
4.所有叶子节点都在同一层，B树是平衡的
5.每个节点的结构为：（n，A0，K1，A1，K2，A2，… ，Kn，An），n为节点中关键字的数量，Kn表示关键字，An表示孩子，它们之间满足升序关系，即A0孩子节点中的所有关键字与所有的孩子的值都小于K1，A1节点中所有的关键字与所有孩子的值都大于K1的值

也就是说，与AVL，红黑树不同，B树的一个节点可以存储多个key值，而AVL，红黑树只能存储一个key值。B树的一个节点能存储的key值个数与其阶数有关，阶数是指一个节点可以拥有的最多的孩子数量。比如一棵1024阶的B树，一个节点可以有1024个孩子，1023个关键字。可以粗略的估算一下，1024阶的B树比较矮胖，它是横向扩展的，一般来说，一棵4层高的1024阶的B树就可以满足存储需求，这个数量级的B树容量能存储千亿级别的关键字

而节点中的关键字与孩子按照升序排序，使得我们可以用二分，或者直接顺序查找，很快的找到某个关键字

搜索逻辑讲解

个人认为，对于某个结构增删查改，先理解它的查找会更好一些。因为学习一个陌生的结构时，先了解的肯定是该结构的性质，而查找某个元素就需要充分的了解这些性质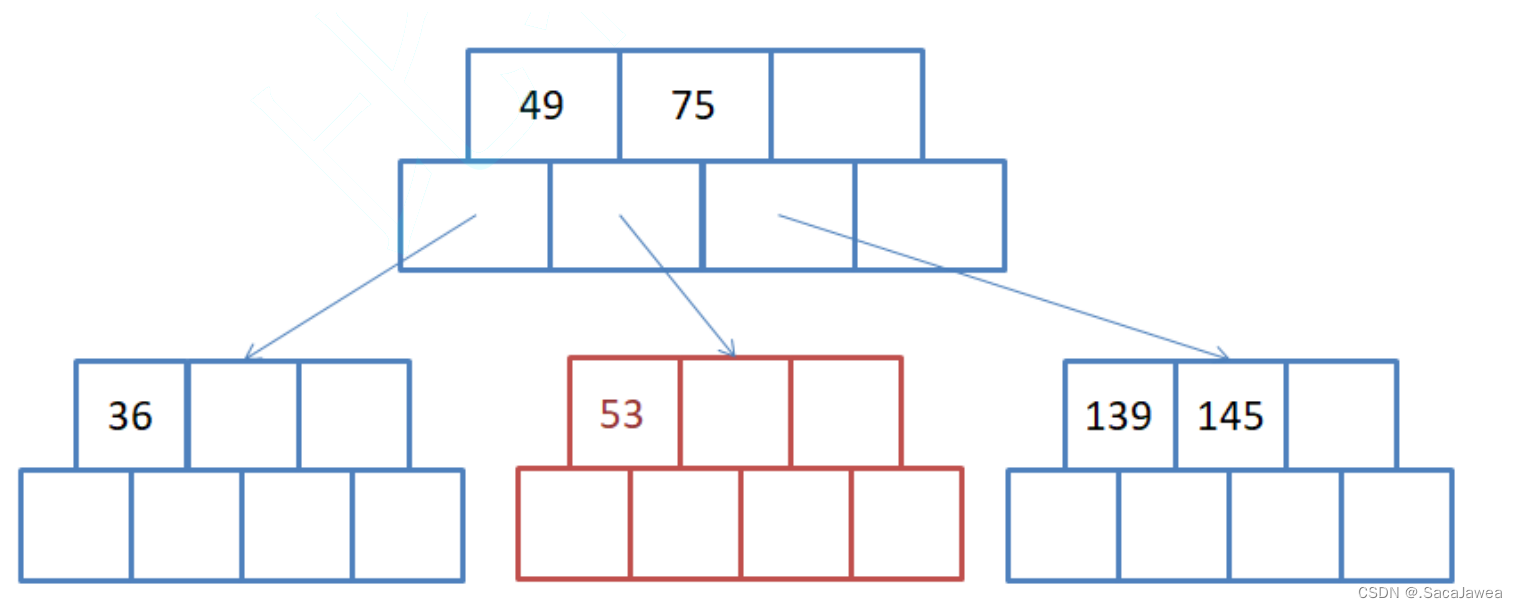
比如要在这棵B树中查找53，先从根节点开始，采用顺序比较，49小于53，说明后面的元素可能有等于53的，所以继续向后比较。75小于53，说明后面的元素都是大于53的，所以停下来，进入孩子节点继续查找（第一个孩子的所有值小于49，而第二个孩子的所有值介于49到75之间，可能含有53，所以进入这个孩子查找）。而这个节点的第一个关键字就是53，查找完成。如果这个节点中没有53，并且可能存在53的孩子节点为空，说明我们查找到叶子节点却没有找到，B树中没有这个元素，查找失败

先交代节点的结构，由于节点需要存储关键字与孩子节点，这两种数据大概率是不同类型的，所以我们使用两个数组分别存储这两种数据，需要注意的是两个数组都比它们应有的长度多了1，这是后续算法的设计需要。并且孩子数组的长度比关键字数组大1，这是B树的性质。除了两个数组，节点还需要存储关键字的数量n，那么n+1就是孩子的数量。最后还要存储一个双亲节点指针，这也是算法设计的需要。关于节点的构造，我们对数组进行初始化，n初始化为0，双亲节点指针也是如此

// 存储k类型的数据，M是B树的阶数
template <class K, size_t M>
struct BTreeNode
{// 孩子与关键字集合// 不过需要多使用一个空间，以方便算法的实现K _keys[M];					 // key的数量最多为M-1BTreeNode* _children[M + 1]; // 孩子的数量为Msize_t _n;					 // n是关键字的数量BTreeNode* _parent;			 // 双亲节点的指针BTreeNode(){for (size_t i = 0; i < M; ++i){_keys[i] = K();_children[i] = nullptr;}_n = 0;_parent = nullptr;_children[M] = nullptr;}
};

根据B树的性质，在关键字数组中，下标为i的节点大于孩子数组中同一下标的孩子，这里有点抽象，不是说关键字大于孩子，而是关键字大于孩子节点中所有的关键字。比如_keys[0]大于_children[0]，小于_children[1]，这样的性质是查找的关键。下面是查找算法的实现

// B树的查找，返回key所在的节点和其在keys数组的下标
// 如果未查找到节点，返回其parent节点与-1
pair<Node*, size_t> Find(const K& key)
{// 从根节点开始遍历Node* cur_node = _root;Node* cur_parent = nullptr;// 遍历分为两层，外层是节点的遍历，当前节点中没有key值，遍历到下一节点// 内层是一个节点的遍历，遍历节点的keys数组while (cur_node){size_t cur_i = 0;// cur是一个节点，现在节点中的keys数组中查找while (cur_i < cur_node->_n){if (key == cur_node->_keys[cur_i]){// 如果相等，直接返回return make_pair(cur_node, cur_i);}else if (key < cur_node->_keys[cur_i]){// 因为keys都是从小到大排列的，如果遇到比key还大的数，说明后面的数都比key大// 此时没必要再往后比较，进入下一个节点遍历break; // 退出当前节点的遍历，进行下一次遍历}else{// 当前的数比key小，后面可能出现等于key的数，继续遍历当前节点cur_i++;}} // while(一个节点的遍历)// 进入下一个节点遍历// 节点的更新与维护cur_parent = cur_node;cur_node = cur_node->_children[cur_i];}// while(整棵树的遍历)// 没有找到返回最后查找的叶子节点return make_pair(cur_parent, -1); 
}

插入逻辑讲解

插入前我们先查找一下，key值是否存在，由于B树不允许键值冗余，所以如果key存在就不进行插入。对于不存在的key值，Find函数会返回这个key应该在的叶子节点（由于当前节点为空，Find的外层循环退出，Find结束。对于一个节点来说，只要你有key值，你就有孩子节点，除非你是叶子节点，所以Find失败是返回一个叶子节点），我们将Find的返回值保存，将key值插入到这个叶子节点中

与搜索同样的，不断地对key进行比较，这是插入排序的单趟排序，将key值插入到keys数组的正确位置上，接着判断keys数组的长度是否在ceil(m/2) - 1 到m - 1之间，如果keys的长度大于m-1，我们就需要对该节点进行分裂。先保存该节点的中间值，接着将中间值往右的所有key值移动到新的节点上，我们将新的节点称为兄弟节点，如果被分裂的节点拥有孩子（不是叶子节点）我们也需要将一半的孩子移动给兄弟节点。兄弟节点构造完成后，将之前保存的之间值插入到它们的双亲节点上，并且将兄弟节点的地址保存到双亲节点的children数组上。

大概总结就是：保存中间值，向右分裂节点，将中间值插入到parent节点中。其中，如果当前节点没有parent节点，即它自己就是根节点，那么我们需要构造一个新的根节点，将中间值放到它的keys[0]上，将两孩子的地址放到children[0]和children[1]上。如果当前节点有parent节点，那么将中间值插入到parent后，只要保存兄弟节点的地址即可，因为当前节点的地址已经被存储在parent中了。至于兄弟节点的地址要怎么保存到parent的children数组中，我们可以拿到中间值在keys数组中的下标，将兄弟节点的地址保存到中间值的右边（children数组中，中间值的下标+1就是中间值的右边）

这里就能理解为什么两个数组的长度要比规定的多1了，因为keys数组如果满了，就无法插入，需要进行分裂，但是分裂节点需要提取中间值，不把key值插入，这个中间值提取就比较困难了。此外，分裂会向parent节点children数组添加孩子，如果一次分裂使得它们的parent节点的keys数组长度达到m，那么children数组就要达到m + 1，否则不满足B树性质。

bool Insert(const K& key)
{// 如果根节点为空，构造根节点，并保存keyif (_root == nullptr){_root = new Node;_root->_keys[0] = key;++(_root->_n);return true;}// 查找是否有相同的值pair<Node*, size_t> ret = Find(key);if (ret.second != -1) // 找到了，不允许键值冗余，返回false{return false;}// 保存当前插入的节点// 因为没有找到的话，Find会返回一个叶子节点，向叶子节点插入Node* cur_node = ret.first;// 将key插入到叶子节点中key_to_node(cur_node, key);// 如果插入后，keys的程度和阶数相等，需要分裂if (cur_node->_n == M){while (true){// 构造一个新的节点Node* brother_node = new Node;// 取出中间值size_t mid = cur_node->_n / 2;K mid_key = cur_node->_keys[mid];// 把右边的值给兄弟size_t j = 0;for (size_t i = mid + 1; i < M; ++i){brother_node->_keys[j++] = cur_node->_keys[i];}// 节点的维护// 注意要减去中间值cur_node->_n -= (j + 1);brother_node->_n += j;brother_node->_parent = cur_node->_parent;// 如果分裂的不是叶子节点，需要分裂孩子if (cur_node->_children[mid + 1] != nullptr){j = 0;// 注意孩子的数量比关键字多1for (size_t i = mid + 1; i <= M; ++i){brother_node->_children[j++] = cur_node->_children[i];}}// 分裂完成// 添加中间值到父节点Node* parent_node = cur_node->_parent;// 如果父节点为空，需要重新构造新的根节点if (parent_node == nullptr){parent_node = new Node;// 记得修改保存的根节点值_root = parent_node;// 将key和两个孩子都插入到根节点parent_node->_keys[0] = mid_key;parent_node->_children[0] = cur_node;parent_node->_children[1] = brother_node;// 父节点的维护cur_node->_parent = _root;brother_node->_parent = _root;++(_root->_n);return true;}// 如果根节点已经存在// 将中间值的key插入，兄弟节点的地址插入key的右边both_to_node(parent_node, mid_key, brother_node);// 如果父节点的keys数组没满，不用分裂，退出循环if (parent_node->_n < M){break;}// 如果此时父节点的keys数组也满了，说明该它也要分裂// 更新父节点，继续循环cur_node = parent_node;} // end of while(true)}return true;
}

其中需要注意的是：添加key值一般就只是添加key值，所以我封装了一个key_to_node接口，接收节点的地址和要插入的key，将key插入指定的节点

// 往指定节点中插入key
size_t key_to_node(Node* dest_node, const K& key)
{int end = dest_node->_n - 1; // 锁定keys的最后一个元素while (end >= 0){// 插入排序，遇到比key大的，往后移动，小的就插入它的后面if (dest_node->_keys[end] <= key){break;}else{dest_node->_keys[end + 1] = dest_node->_keys[end];}--end;}dest_node->_keys[end + 1] = key;++(dest_node->_n);return end + 1;
}

这就是插入排序的单趟排序的逻辑，此外，如果进行了分裂，那么就需要提取中间值到parent节点中。如果parent不存在，就先构造一个再把两个孩子的地址插入到parent中。但parent存在的话，就只要将兄弟节点的地址插入到parent中，为什么被分裂的节点地址不需要插入？因为该地址可能在构造parent时，与兄弟节点地址一起插入parent了，所以这里只要将兄弟的地址插入到中间值的右边，这里我封装了both_to_node接口，将key和一个节点地址插入到指定节点的右边

void both_to_node(Node* dest_node, const K& key, Node* child)
{// key的插入，注意返回值的保存size_t cur_i = key_to_node(dest_node, key) + 1;// 将child插入到key的右孩子处// 锁定最后一个孩子，移动size_t end = dest_node->_n - 1;// 移动children数组，将child存储到数组中while (end >= cur_i){dest_node->_children[end + 1] = dest_node->_children[end];--end;}dest_node->_children[cur_i] = child;
}

B树的整体实现，文件展示

#pragma once#include 
#include 
#include 
using namespace std;// 存储k类型的数据，M是B树的阶数
template <class K, size_t M>
struct BTreeNode
{// 孩子与关键字集合// 不过需要多使用一个空间，以方便算法的实现K _keys[M]; // key的数量最多为M-1BTreeNode* _children[M + 1]; // 孩子的数量为Msize_t _n; // n是关键字的数量BTreeNode* _parent; // 双亲节点的指针BTreeNode(){for (size_t i = 0; i < M; ++i){_keys[i] = K();_children[i] = nullptr;}_n = 0;_parent = nullptr;_children[M] = nullptr;}
};template <class K, size_t M>
class BTree
{
public:typedef BTreeNode<K, M> Node;
private:// B树的查找，返回key所在的节点和其在keys数组的下标pair<Node*, size_t> Find(const K& key){// 从根节点开始遍历Node* cur_node = _root;Node* cur_parent = nullptr;while (cur_node){size_t cur_i = 0;// cur是一个节点，现在节点中的keys数组中查找while (cur_i < cur_node->_n){if (key == cur_node->_keys[cur_i]){// 如果相等，直接返回return make_pair(cur_node, cur_i);}else if (key < cur_node->_keys[cur_i]){// 因为keys都是从小到大排列的，如果遇到比key还大的数，说明后面的数都比key大// 此时没必要再往后比较，进入下一个节点遍历break; // 退出当前节点的遍历，进行下一次遍历}else{// 当前的数比key小，后面可能出现等于key的数，继续遍历当前节点cur_i++;}} // while(一个节点的遍历)// 进入下一个节点遍历cur_parent = cur_node;cur_node = cur_node->_children[cur_i];}// while(整棵树的遍历)return make_pair(cur_parent, -1); // 没有找到返回最后查找的叶子节点}// 往指定节点中插入keysize_t key_to_node(Node* dest_node, const K& key){int end = dest_node->_n - 1; // 锁定keys的最后一个元素while (end >= 0){// 插入排序，遇到比key大的，往后移动，小的就插入它的后面if (dest_node->_keys[end] <= key){break;}else{dest_node->_keys[end + 1]  = dest_node->_keys[end];}--end;}dest_node->_keys[end + 1] = key;++(dest_node->_n);return end + 1;}void both_to_node(Node* dest_node, const K& key, Node* child){// key的插入，注意返回值的保存size_t cur_i = key_to_node(dest_node, key) + 1;// 将child插入到key的右孩子处// 锁定最后一个孩子，移动size_t end = dest_node->_n - 1;// 移动children数组，将child存储到数组中while (end >= cur_i) {dest_node->_children[end + 1] = dest_node->_children[end];--end;}dest_node->_children[cur_i] = child;}public://  key值的插入bool Insert(const K& key){// 如果根节点为空，构造根节点，并保存keyif (_root == nullptr){_root = new Node;_root->_keys[0] = key;++(_root->_n);return true;}// 查找是否有相同的值pair<Node*, size_t> ret = Find(key);if (ret.second != -1) // 找到了，不允许键值冗余，返回false{return false;}// 保存当前插入的节点// 因为没有找到的话，Find会返回一个叶子节点，向叶子节点插入Node* cur_node = ret.first;// 将key插入到叶子节点中key_to_node(cur_node, key);// 如果插入后，keys的程度和阶数相等，需要分裂if (cur_node->_n == M){while (true){// 构造一个新的节点Node* brother_node = new Node;// 取出中间值size_t mid = cur_node->_n / 2;K mid_key = cur_node->_keys[mid];// 把右边的值给兄弟size_t j = 0;for (size_t i = mid + 1; i < M; ++i){brother_node->_keys[j++] = cur_node->_keys[i];}// 节点的维护// 注意要减去中间值cur_node->_n -= (j + 1);brother_node->_n += j;brother_node->_parent = cur_node->_parent;// 如果分裂的不是叶子节点，需要分裂孩子if (cur_node->_children[mid + 1] != nullptr){j = 0;// 注意孩子的数量比关键字多1for (size_t i = mid + 1; i <= M; ++i){brother_node->_children[j++] = cur_node->_children[i];}}// 分裂完成// 添加中间值到父节点Node* parent_node = cur_node->_parent;// 如果父节点为空，需要重新构造新的根节点if (parent_node == nullptr){parent_node = new Node;// 记得修改保存的根节点值_root = parent_node;// 将key和两个孩子都插入到根节点parent_node->_keys[0] = mid_key;parent_node->_children[0] = cur_node;parent_node->_children[1] = brother_node;// 父节点的维护cur_node->_parent = _root;brother_node->_parent = _root;++(_root->_n);return true;}// 如果根节点已经存在// 将中间值的key插入，兄弟节点的地址插入key的右边both_to_node(parent_node, mid_key, brother_node);// 如果父节点的keys数组没满，不用分裂，退出循环if (parent_node->_n < M){break;}// 如果此时父节点的keys数组也满了，说明该它也要分裂// 更新父节点，继续循环cur_node = parent_node;} // end of while(true)}return true;}// for testvoid level_order(){queue<Node*> for_print;for_print.push(_root);size_t lev_size = 1;while (!for_print.empty()){while (lev_size){Node* cur_node = for_print.front();for_print.pop();--lev_size;size_t i = 0;for (i = 0; i < cur_node->_n; ++i){cout << cur_node->_keys[i] << ' ';if (cur_node->_children[i])for_print.push(cur_node->_children[i]);}if (cur_node->_children[i])for_print.push(cur_node->_children[i]);cout << "| ";}cout << endl;lev_size = for_print.size();}}
private:Node* _root = nullptr; // 一颗B树的根节点
};

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！