【数据结构】初识二叉树
目录
前言（为什么要有树）
1数的概念
2树的相关概念
3二叉树的定义
4树的存储方式
5.二叉树的特点
前言（为什么要有树）
我们在数前面已经学了许多数据结构，顺序表，链表，栈，队列。但是他们都有一个特点那就是，他们通常存储具有线性关系的数据，而在实际应用中许多逻辑结构并不是简单线性结构，常常存在着一对多，甚至多对多的情况。如：企业里的职级关系。族谱……
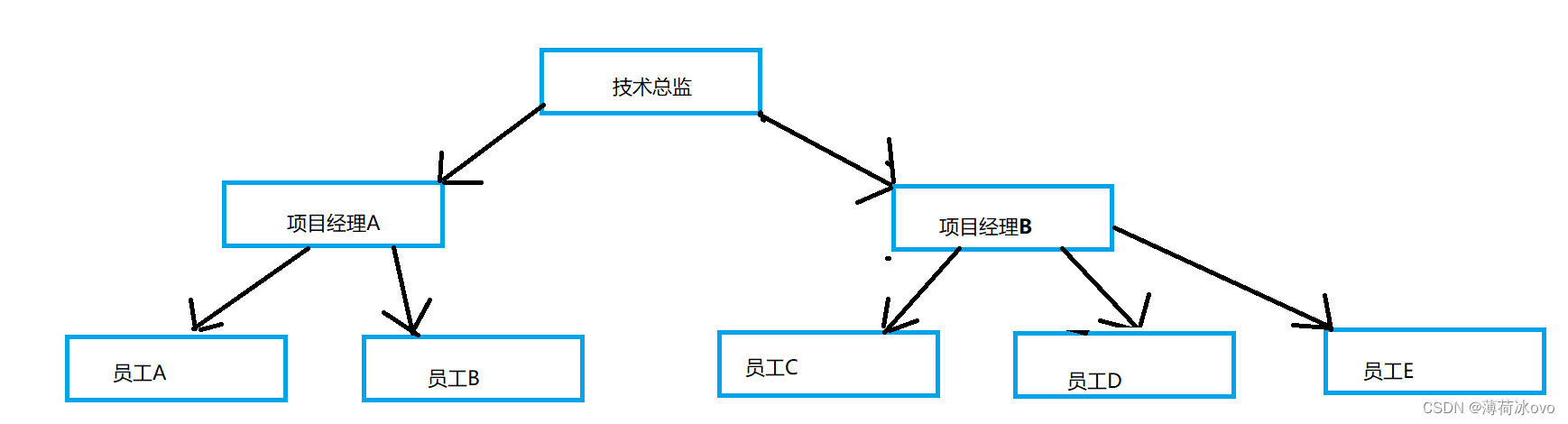
这种由同一个根向下衍生的结构就被成为树；
1数的概念
树是一种 非线性 的数据结构，它是由 n （ n>=0 ）个有限结点组成一个具有层次关系的集合。 把它叫做树是因 为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的 。
- 有一个特殊的结点，称为根结点，根节点没有前驱结点
- 除根节点外，其余结点被分成M(M>0)个互不相交的集合T1、T2、……、Tm，其中每一个集合Ti(1<= i <= m)又是一棵结构与树类似的子树。每棵子树的根结点有且只有一个前驱，可以有0个或多个后继
- 因此，树是递归定义的。
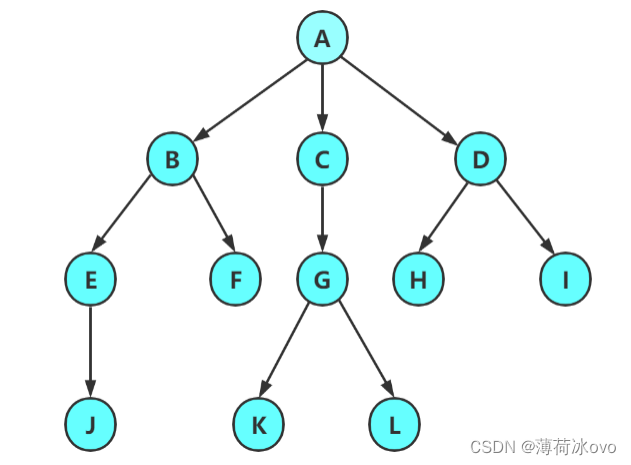
注意：树形结构中，子树之间不能有交集，否则就不是树形结构
2树的相关概念
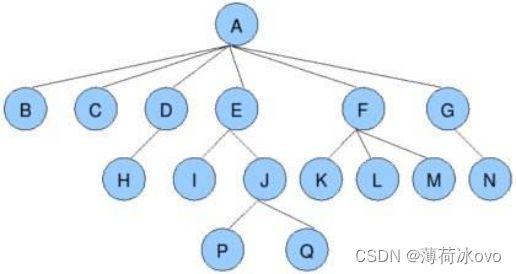
3二叉树的定义
二叉树是树的一种特殊形式，二叉，顾名思义，这种树每个节点累计最多有两个节点
任意二叉树都只有以下的情况
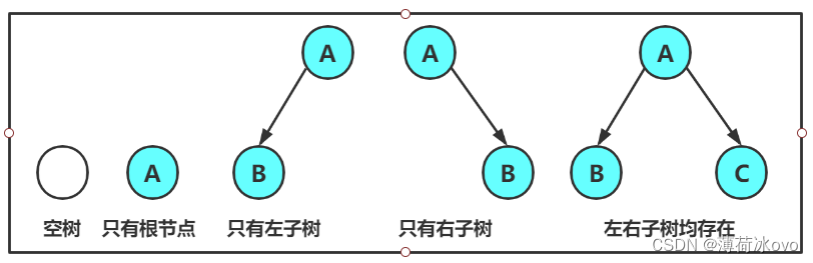
此外二叉树还有两种特殊形式，一个叫满二叉树，一个叫做完全二叉树。
1. 满二叉树 ：一个二叉树，如果每一个层的结点数都达到最大值，则这个二叉树就是满二叉树。也就是 说，如果一个二叉树的层数为K ，且结点总数是 ，则它就是满二叉树。 2. 完全二叉树 ：完全二叉树是效率很高的数据结构，完全二叉树是由满二叉树而引出来的。对于深度为 K 的，有n 个结点的二叉树，当且仅当其每一个结点都与深度为 K 的满二叉树中编号从 1 至 n 的结点一一对 应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树。
4树的存储方式
数据结构的的存储分为物理结构和逻辑结构，树属于逻辑结构，可以用多种物理方式表达。
1链式储存结构
2数组
在链式结构中有很多种表示方式如：双亲表示法，孩子表示法、孩子双亲表示法以及孩子兄弟表示法 等。我们这里就简单的了解其中最常用的孩子兄弟表示法。这也是二叉树最直观的储存方式，
typedef int DataType;
struct Node
{struct Node* _firstChild1; // 第一个孩子结点struct Node* _pNextBrother; // 指向其下一个兄弟结点DataType _data; // 结点中的数据域
};
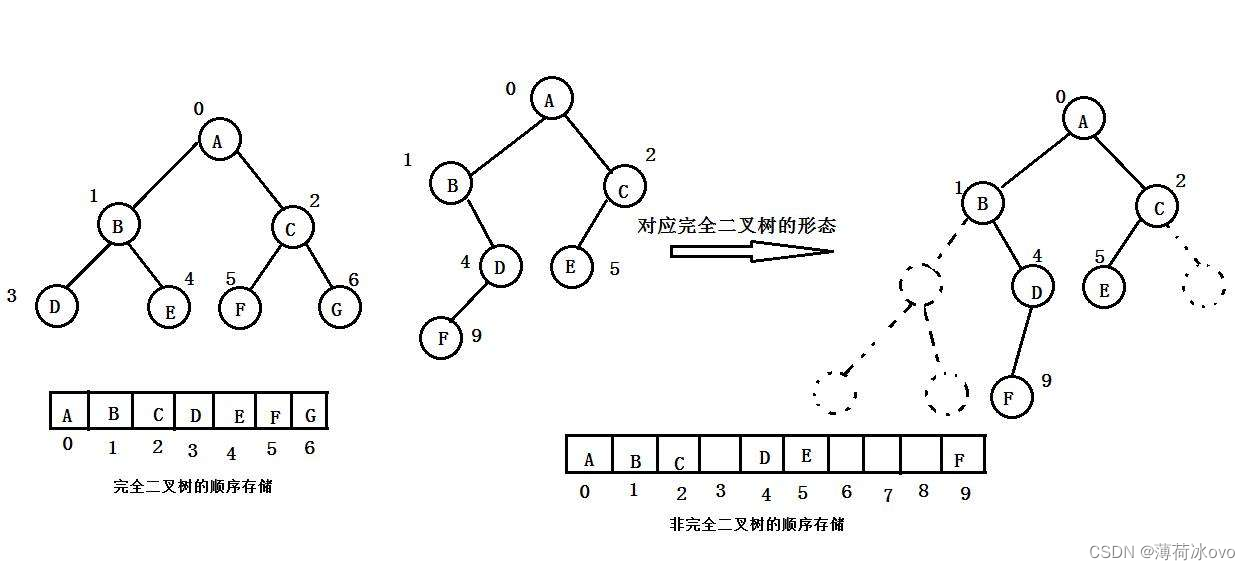那么用数组存储如何找到左右孩子节点？
假设一个父节点的下标为parent，那么他的左孩子节点的下标为2*parent+1,右孩子节点下表为2*parent+2，反过来假设一个子节点的下标为child,那他的父节点的下表为（child-1）/2.
5.二叉树的特点
1. 若规定根节点的层数为1，则一棵非空二叉树的第i层上最多有 2^(i-1)个结点. 2. 若规定根节点的层数为1，则深度为h的二叉树的最大结点数是2^h - 1. 3. 对任何一棵二叉树, 如果度为0其叶结点个数为 n0, 度为2的分支结点个数为n2 ,则有 n0＝ n2＋1 4. 若规定根节点的层数为1，具有n个结点的满二叉树的深度，h=本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！