第二期第五周周报
第一题,巨大的牛棚:
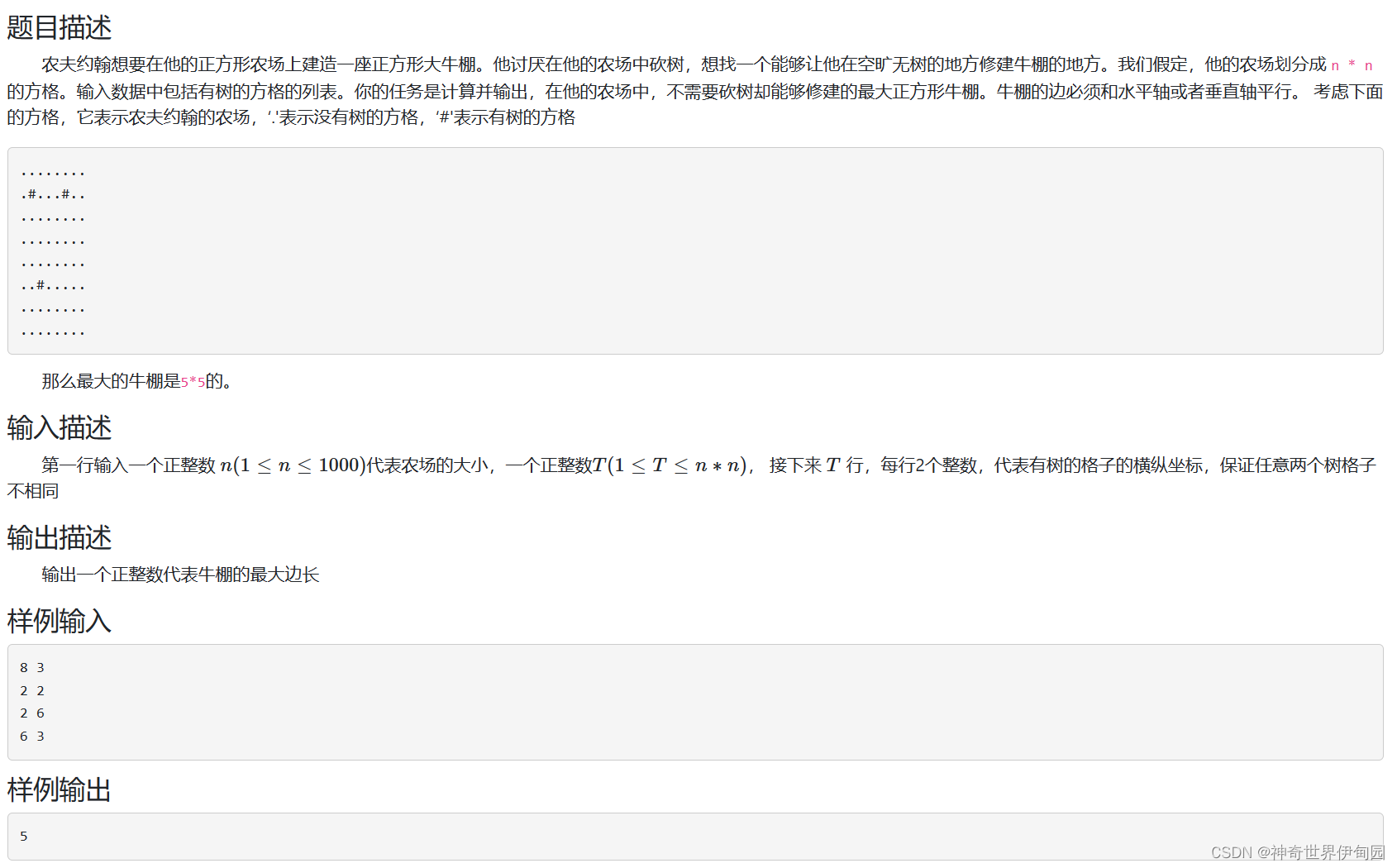
和迷宫题类似的dp法,截止到某一个点的边长长度与其上方,左方,左上方的长度有关。三者中取最小值+1。如果碰到#就记为0
#include
using namespace std;
int n, t, arr[1005][1005], ans, dp[1005][1005];
int main()
{cin >> n >> t;while(t--){int a, b;cin >> a >> b;arr[a][b] = 1;}for(int i = 1; i <= n; ++i){for(int j = 1; j <= n; ++j){if(!arr[i][j]){dp[i][j] = min(dp[i-1][j-1], min(dp[i-1][j], dp[i][j-1]))+1;ans = max(dp[i][j], ans);}}}cout << ans << endl;return 0;
} 第二题,高利贷
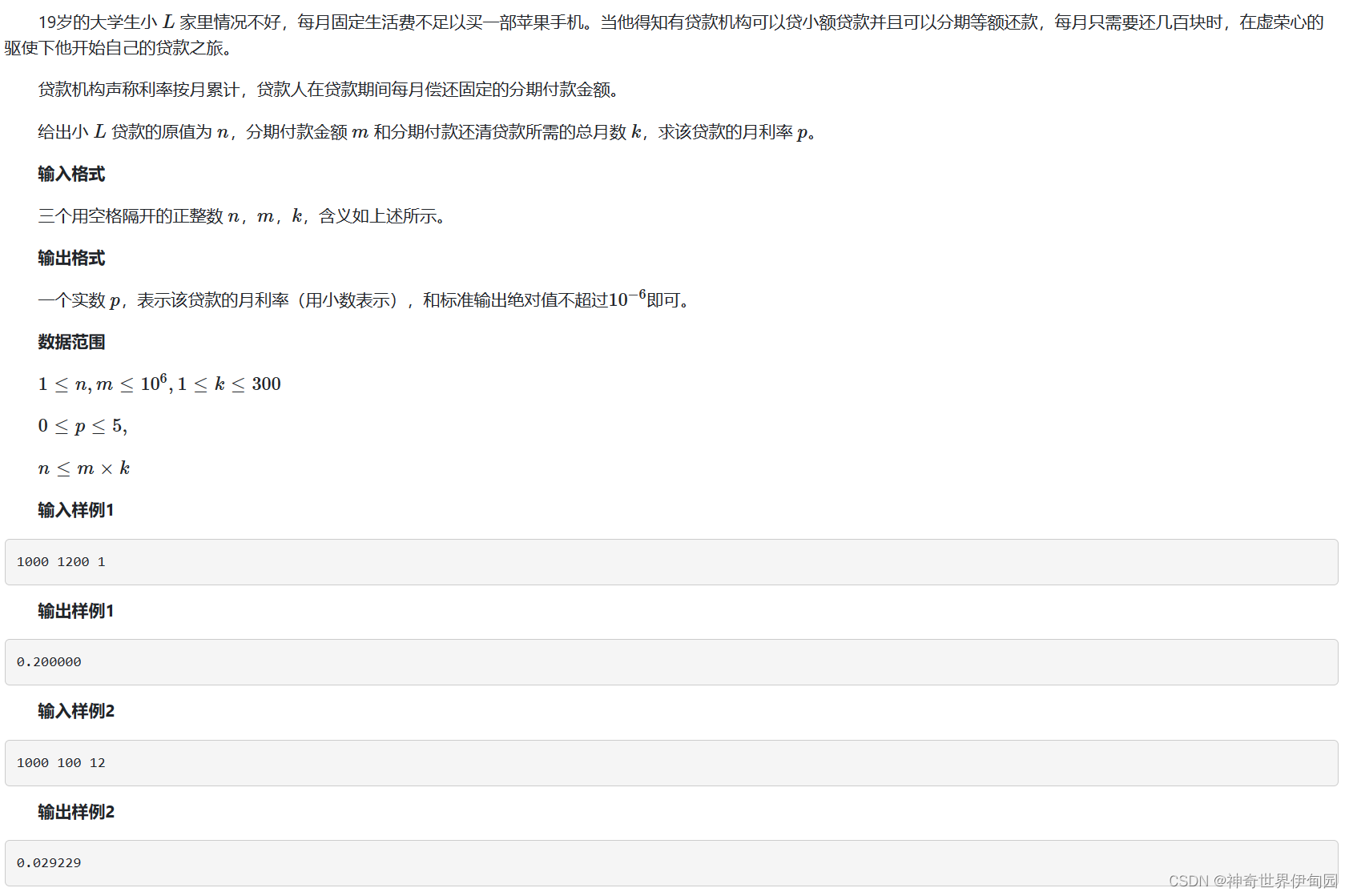
 本来以为是数学运算,其实我们只需要根据题意列出方程然后,找到一个解的范围二分法求近似解即可。利率不一定是小于1的(真就高利贷),这个方程也不是很难列。浮点结果运算多半就是二分。和以前周赛的解方程题差不多。
本来以为是数学运算,其实我们只需要根据题意列出方程然后,找到一个解的范围二分法求近似解即可。利率不一定是小于1的(真就高利贷),这个方程也不是很难列。浮点结果运算多半就是二分。和以前周赛的解方程题差不多。
#include
using namespace std;int n, m, k;
bool check(double p)
{double s = 0, mul = m;for(int i = 1; i <= k; ++i){mul /= (1+p);s += mul;}if(s >= n){return 0;}else{return 1;}
}
int main()
{cin >> n >> m >> k;double l = 0, r = m*k/n-0.95, mid; //比最坏的情况多一点while(fabs(r-l) >= 5E-7){mid = (l+r)/2;if(check(mid)) //结果比较大了{r = mid-1E-7;}else //比较小{l = mid+1E-7;}}printf("%.6lf", mid);return 0;
} 第三题 背包:
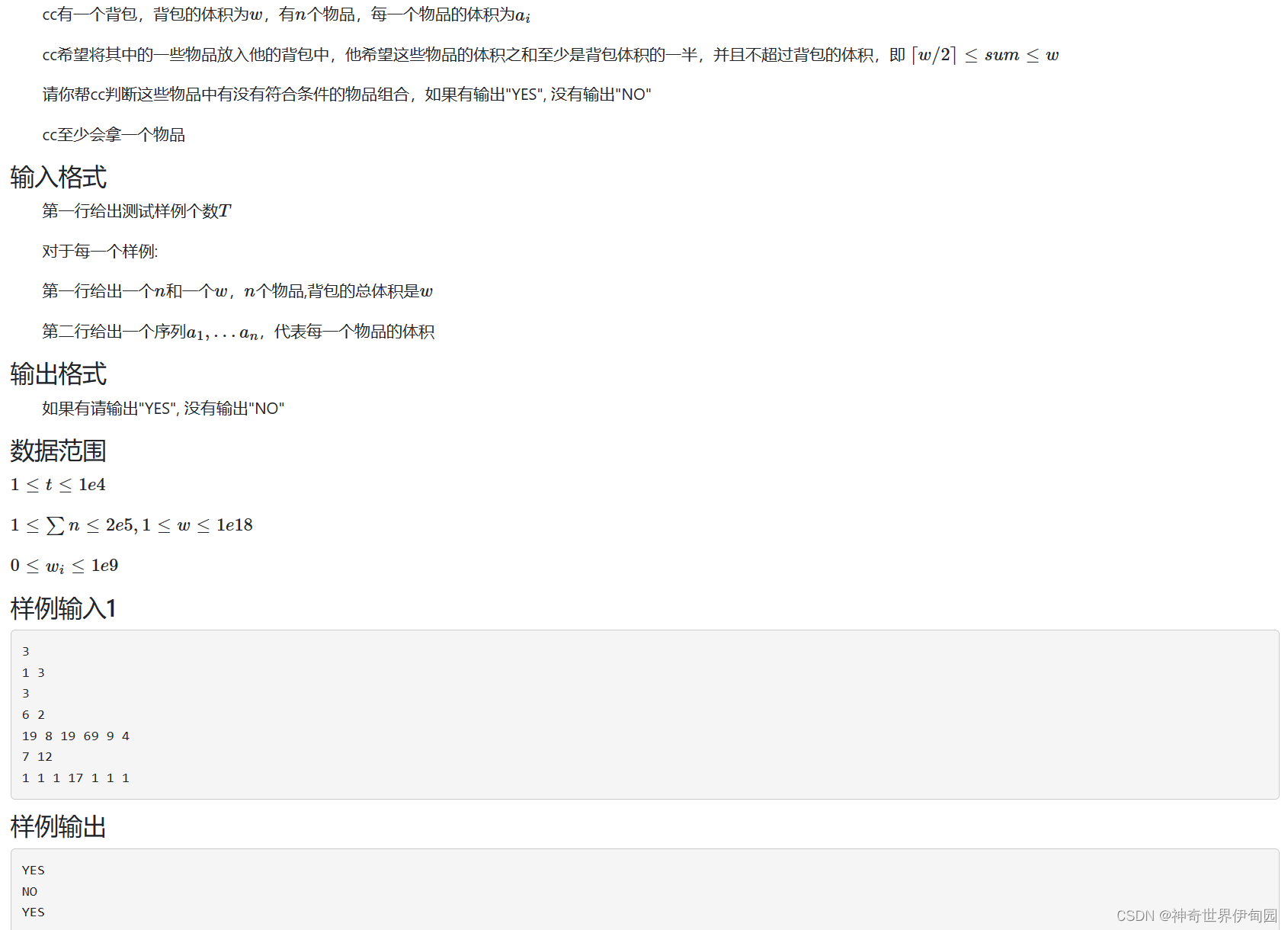
如果背包内存在这样一个物品那么就是true了。如果每个物品都比w大那么就是false了。相反,如果不存在这样一个物品但是存在比w/2小的物品,就逐个累加求和即可。小技巧:向上取整能用(w+1)/2来取代。还有要开long long
#include
#define endl '\n'
#define int long long
using namespace std;
const int MAXN = 2E5+10;
int t;
int n, w;
signed main() //数据范围大,不开ll见祖宗
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin >> t;while(t--){int flag = 0, sum = 0;cin >> n >> w;while(n--){int num;cin >> num; //小技巧,用(w+1)/2代替向上取整if(num >= (w+1)/2 && num <= w){flag = 1;}else if(num < (w+1)/2){sum += num;}if(sum >= (w+1)/2 && sum <= w){flag = 1;}}if(flag){cout << "YES" << endl;}else{cout << "NO" << endl;}}return 0;
} 第四题 三回文序列
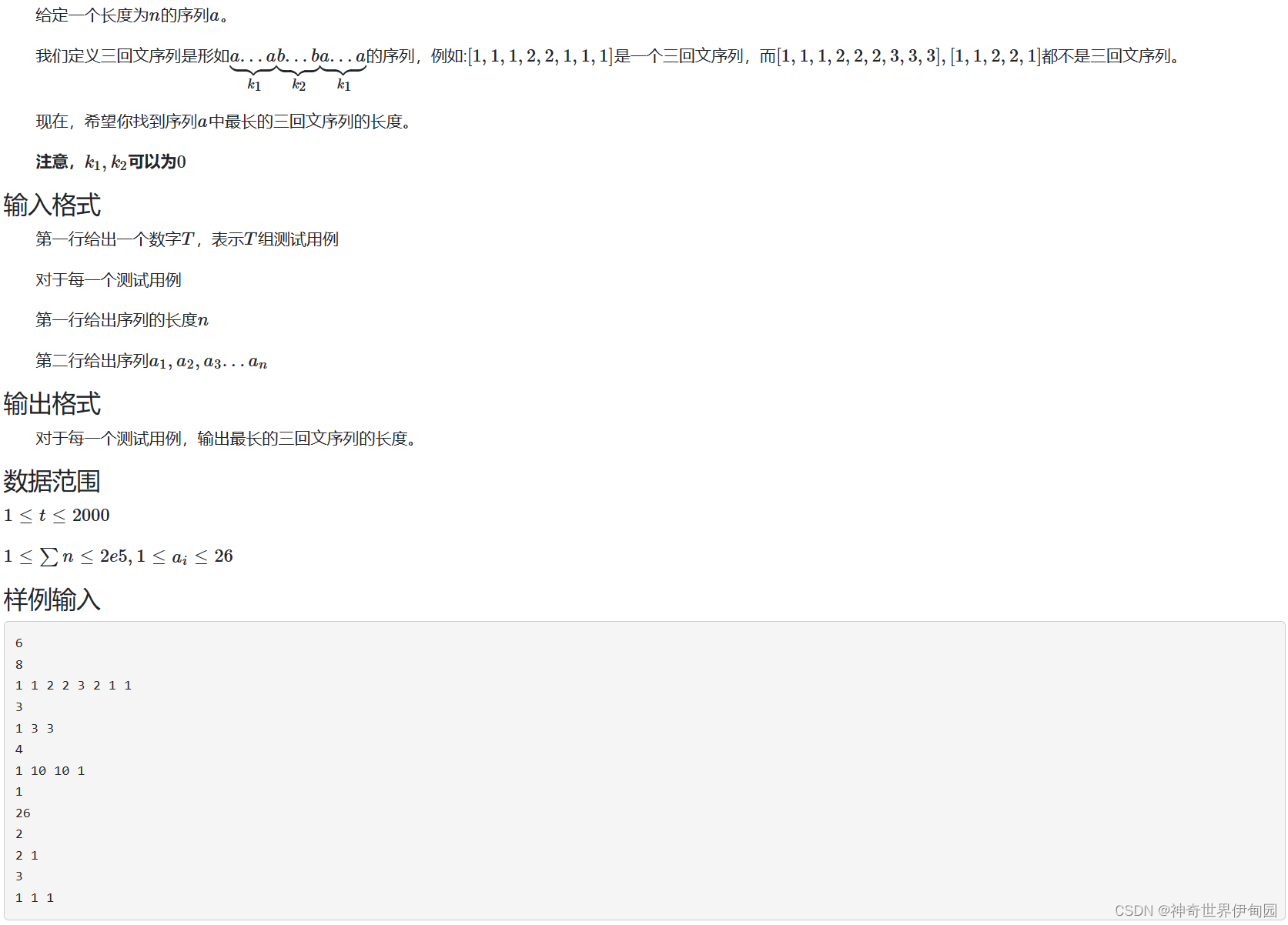
 这个题有点难度,由于数值的范围比较小所以可以枚举数据然后匹配。需要记住每个数值第i次出现的位置。然后还有前缀和sum[i][j]表示前i个字符中j字符出现的次数。枚举时首先枚举两边的情况,看看最多出现多少个且不碰到一起,然后再枚举中间的字符,看哪个字符出现的最多。注意二回文序列也是特殊的三回文序列。
这个题有点难度,由于数值的范围比较小所以可以枚举数据然后匹配。需要记住每个数值第i次出现的位置。然后还有前缀和sum[i][j]表示前i个字符中j字符出现的次数。枚举时首先枚举两边的情况,看看最多出现多少个且不碰到一起,然后再枚举中间的字符,看哪个字符出现的最多。注意二回文序列也是特殊的三回文序列。
#include
using namespace std;
const int max_num = 26;
const int max_len = 2e5;int sum[max_num + 1][max_len + 1], indices[max_num + 1][max_len + 1];int main() {int t, n, x;cin >> t;for (int i = 0; i < t; i++) {cin >> n;for (int j = 1; j <= n; j++) {cin >> x;for (int k = 1; k <= max_num; k++) {sum[k][j] = sum[k][j - 1];}sum[x][j]++;indices[x][sum[x][j]] = j;}int ans = 0;for (int a = 1; a <= 26; a++) {for (int k1 = 0; k1 <= sum[a][n]; k1++) {int l, r;if (k1) {l = indices[a][k1];r = indices[a][sum[a][n] - k1 + 1];}else {l = 0;r = n + 1;}if (l > r) break;else if (l == r) ans = max(ans, 2 * k1 - 1);else {for (int b = 1; b <= 26; b++) {int k2 = sum[b][r - 1] - sum[b][l];ans = max(ans, k1 * 2 + k2);}}}}cout << ans << endl;}return 0;
} 第五题 简单的异或问题
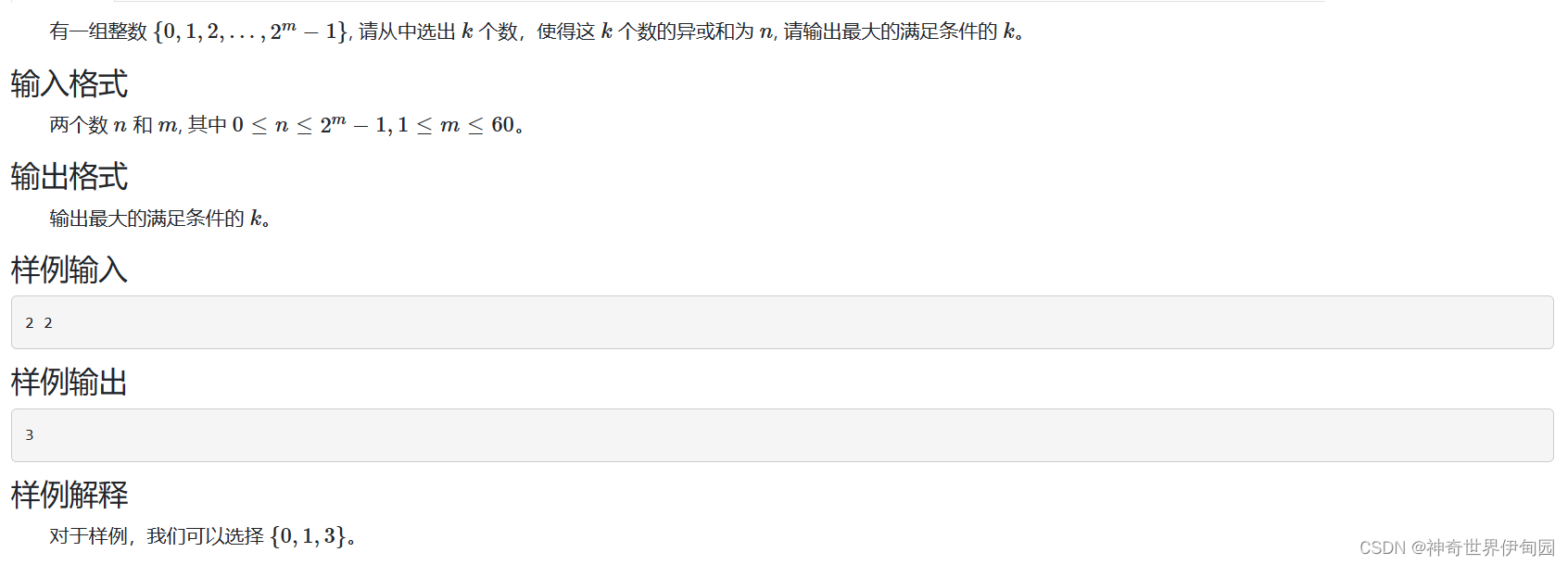
这题的样例具有迷惑性。首先明白的是这样的范围内每个数和他相补的数异或结果为其最大值(比如0和255,1和254) ,转化为二进制是全1,两个全1的数异或就是0,全1的数和其他数异或可以得到自己。所有的数异或起来就是0,但是如果只有2个数(0和1)那么异或起来就是1了。
#include
#define int long long
using namespace std;
int n, m, k;signed main()
{cin >> n >> m; //0^1 == 1if(n == 0){if(m > 1){cout << (int)pow(2, m);}else{cout << 1;}}else{if(m > 1){cout << (int)pow(2, m)-1;}else{cout << 2;}}return 0;
} 第六题 字串的循环挪动
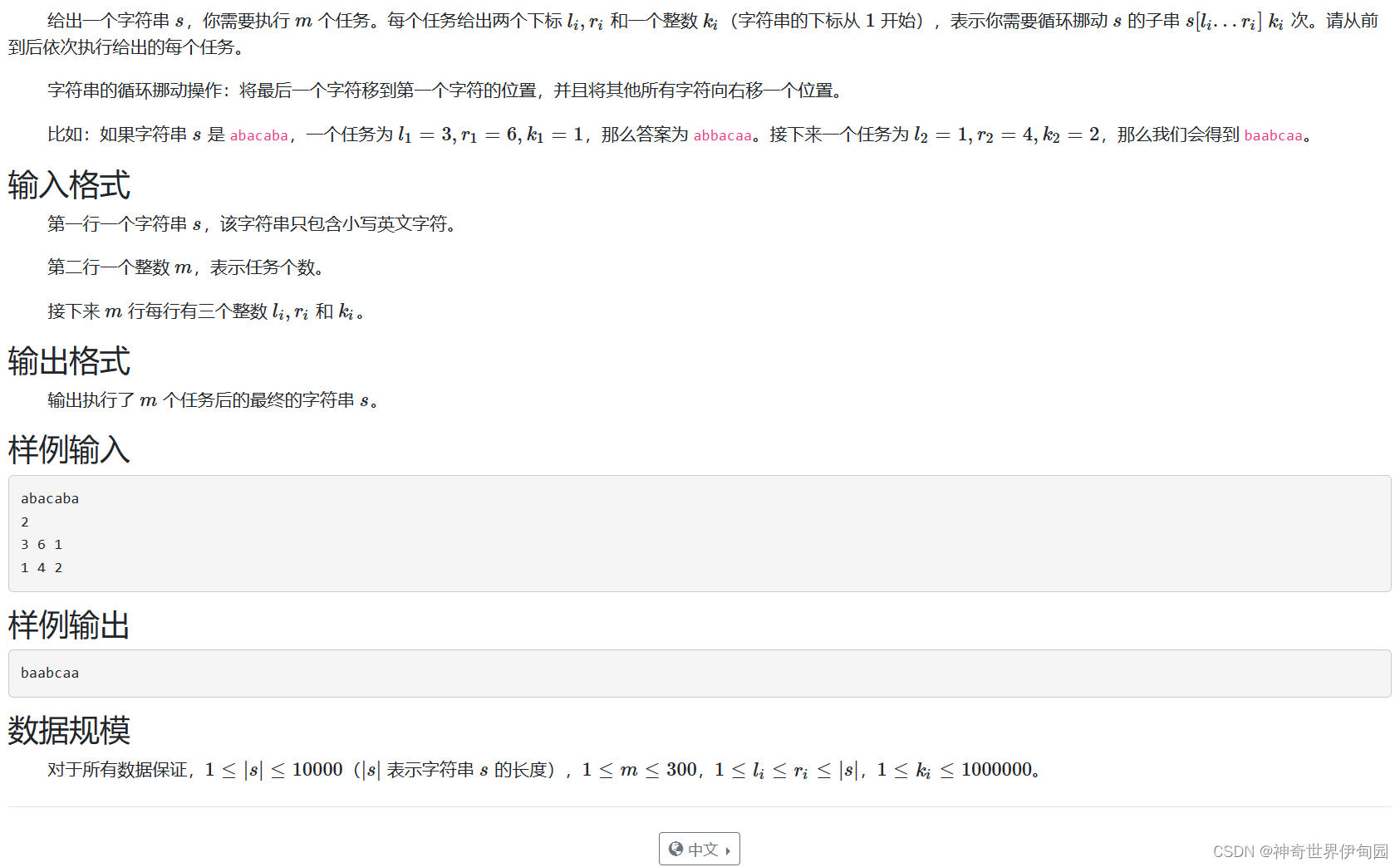
看到这题我就想起了队列。这题其实很简单,只要按照要求首尾循环挪动即可。但是由于挪动的次数比较多所以要对字符串的长度进行取余然后再挪动。
#include
using namespace std;string str;
int m;
//这一题还是比较简单的,substr
int main()
{ios::sync_with_stdio(0);cin.tie(0), cout.tie(0);cin >> str >> m;while(m--){int l, r, k;cin >> l >> r >> k;--l, --r;string sub = str.substr(l, r-l+1);k %= sub.size();while(k--){char c = sub.back();sub.pop_back();sub = c+sub;}str.replace(l, r-l+1, sub);}cout << str << endl;return 0;
} 第七题 弗拉德和糖果II
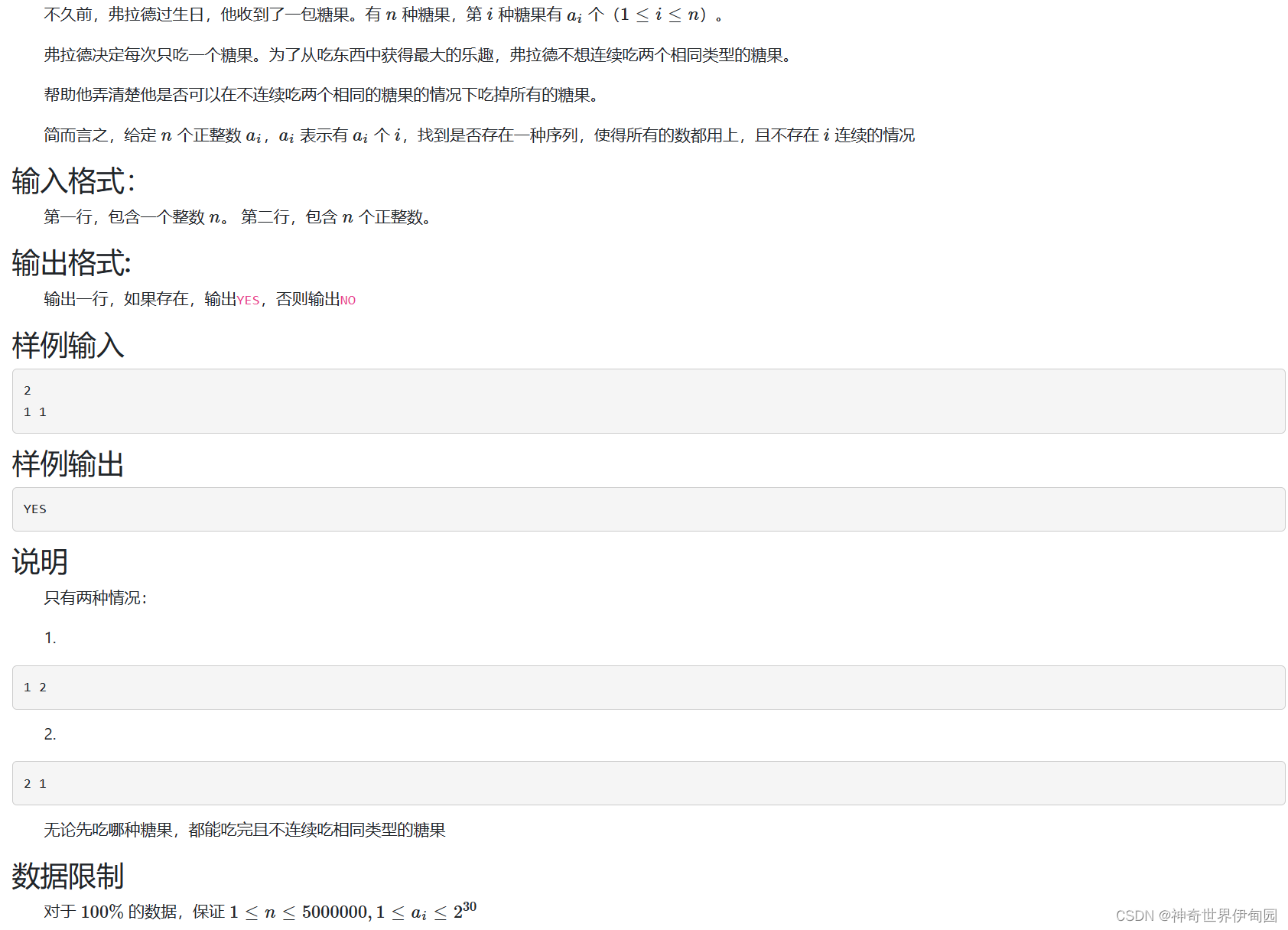
首先吃最多的糖果同时在来吃其他类型的糖果。如果最多的糖果没吃完其他糖果就已经吃完了,肯定是不行的。相反,如果最多的糖果吃完了其他糖果刚好吃完,肯定行。如果最多的糖果没有其他糖果加起来多,可以考虑把其他糖果总数吃的和最多的糖果一样多然后再来吃。比较最多的糖果和其他糖果总和就行,这题算是贪心
#include
#define int long long
using namespace std;
int n, sum;
signed main()
{ios::sync_with_stdio(0);cin.tie(0);cin >> n;vector arr(n);for(int i = 0; i < n; ++i){cin >> arr[i];}sort(arr.begin(), arr.end()); //从小到大排序for(int i = 0; i < n-1; ++i){sum += arr[i];}if(arr[n-1] > sum && n != 1){cout << "NO" << endl;}else{cout << "YES" << endl;}return 0;
} 第八题 上帝的集合
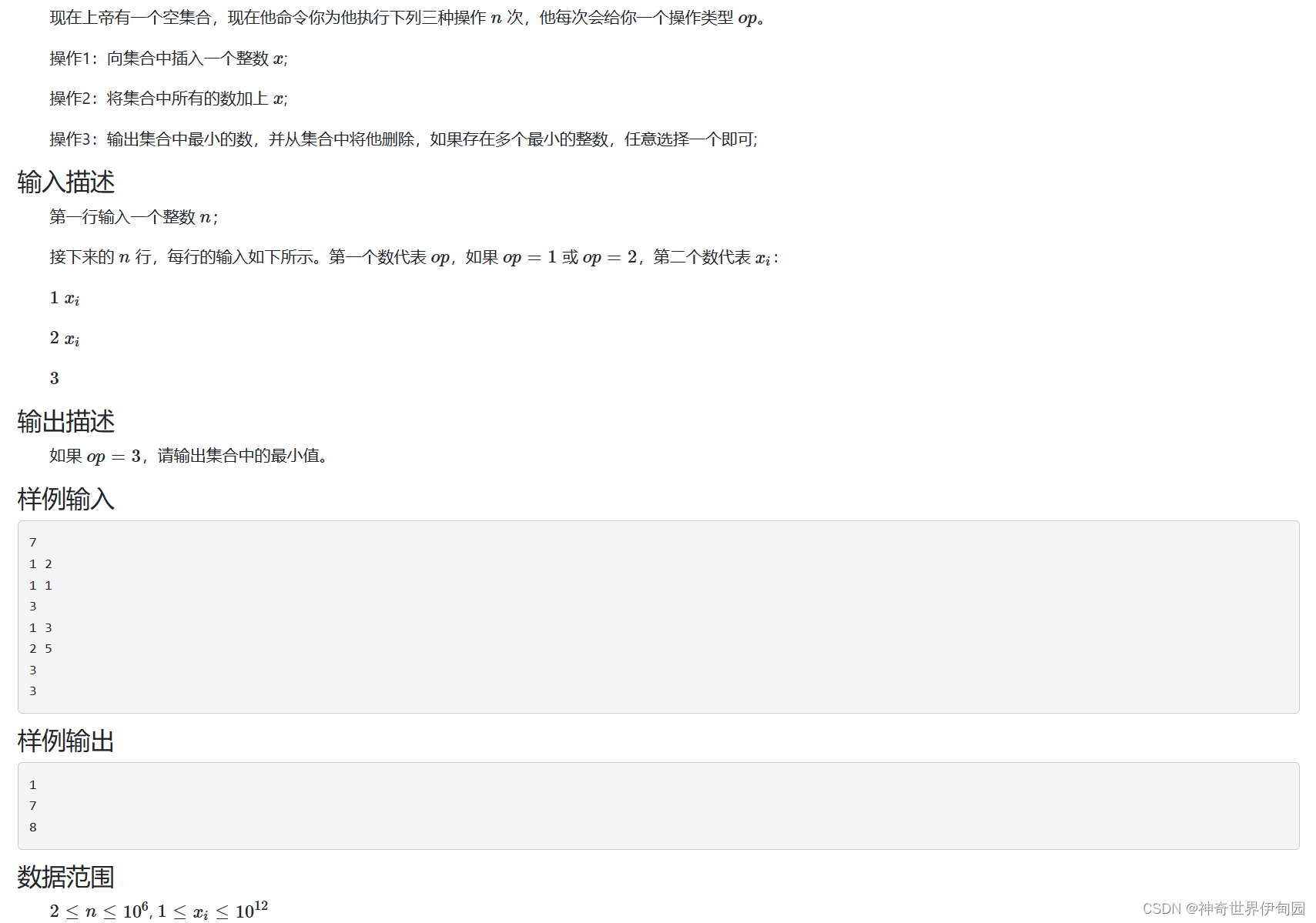
使用multiset来维护集合。我发现multiset的从迭代器访问的第一个元素不一定是最小的,可以使用lower_bound(LONG_LONG_MIN)来得到最小的元素。此外由于可能进行多次加操作,如果加操作每次都对每个元素做可能会超时,所以我们要记住总共加了多少,然后新插入的元素没有进行加操作,所有就相对其他元素是减了。保持每个元素相对值不变即可。此外或许使用map来维护集合。map可以根据键值自动排序,然后记录元素出现的次数。
#include
#define int long long
#define endl '\n'
using namespace std;
int n, sum;
//总共加了多少个数
//需要使用multiset
multiset s;
signed main()
{ios::sync_with_stdio(0);cin.tie(0), cout.tie(0);cin >> n;while(n--){int op, x;cin >> op;if(op == 1){cin >> x;s.insert(x-sum);}else if(op == 2){cin >> x;sum += x;}else{auto it = s.lower_bound(LONG_LONG_MIN); //返回>=给定值的最小值迭代器cout << *it+sum << endl;s.erase(it);}}return 0;
} 第九题 最长公共子序列
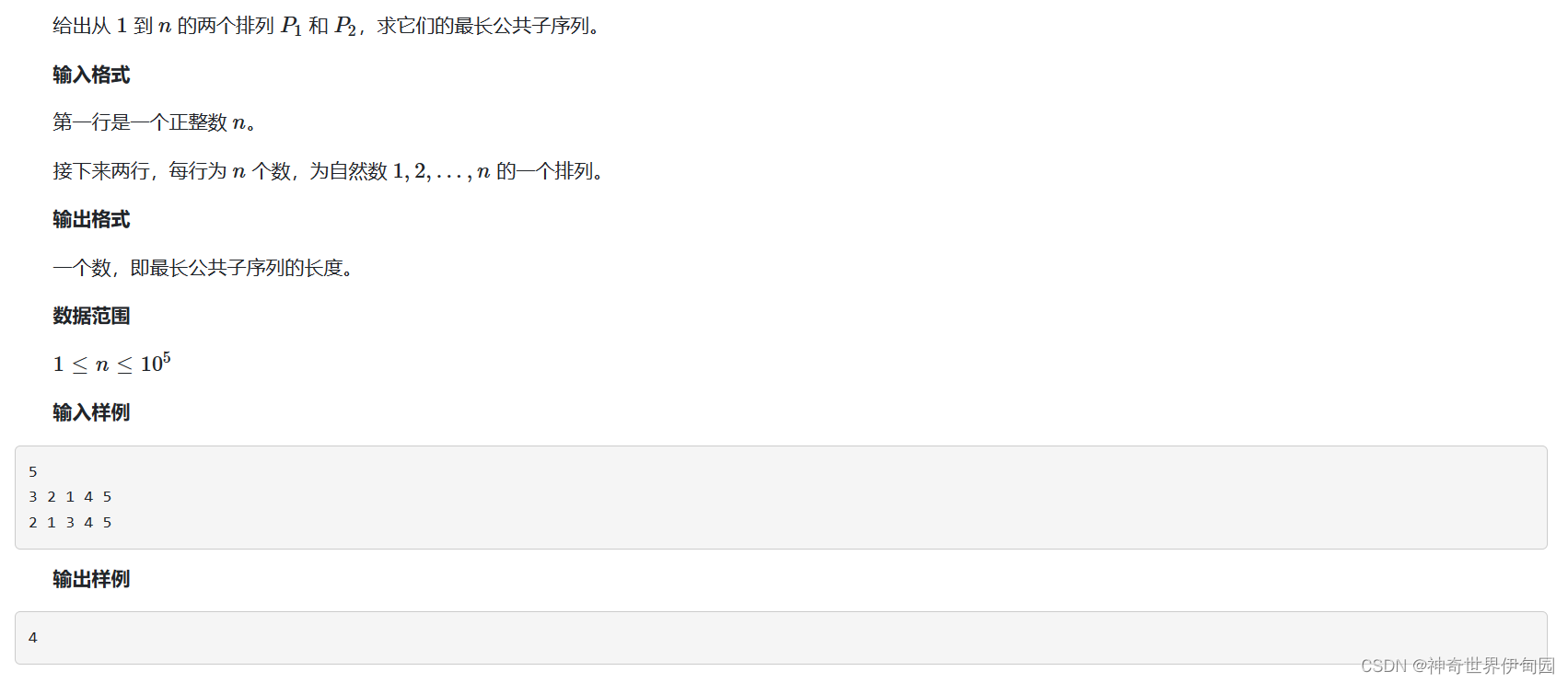
应该是最难的了。可以用O(n2)的方法来dp两个集合公共子序列的长度,但是会TLE。考虑到这两个数列的元素都是1-n的自然数,只要第二个数列子序列的元素在第一个序列中的位置是单调递增即可,找到这样一个子序列,但是二分查找这点思路我还是不太明白。但是感觉这个有点道理的样子。可以当作板子记下。lower_bound和upper_bound可以实现线性数据结构的二分查找,长知识了。
#include
using namespace std;
const int N=100010;
int n,len,a[N],m[N],b[N],f[N];
int main()
{scanf("%d",&n);for (int i=1;i<=n;i++) {scanf("%d",&a[i]);m[a[i]]=i;}for (int i=1;i<=n;i++){scanf("%d",&b[i]);f[i]=99999999;}f[0]=0;for (int i=1;i<=n;i++){if (m[b[i]]>f[len]) f[++len]=m[b[i]];else{int k=lower_bound(f+1,f+1+len,m[b[i]])-f; //这段代码相当于一串二分查找,就是寻找f[]中第一个大于等于m[b[i]]的数的位置f[k]=min(m[b[i]],f[k]);} }cout< 第十题 喵喵序列
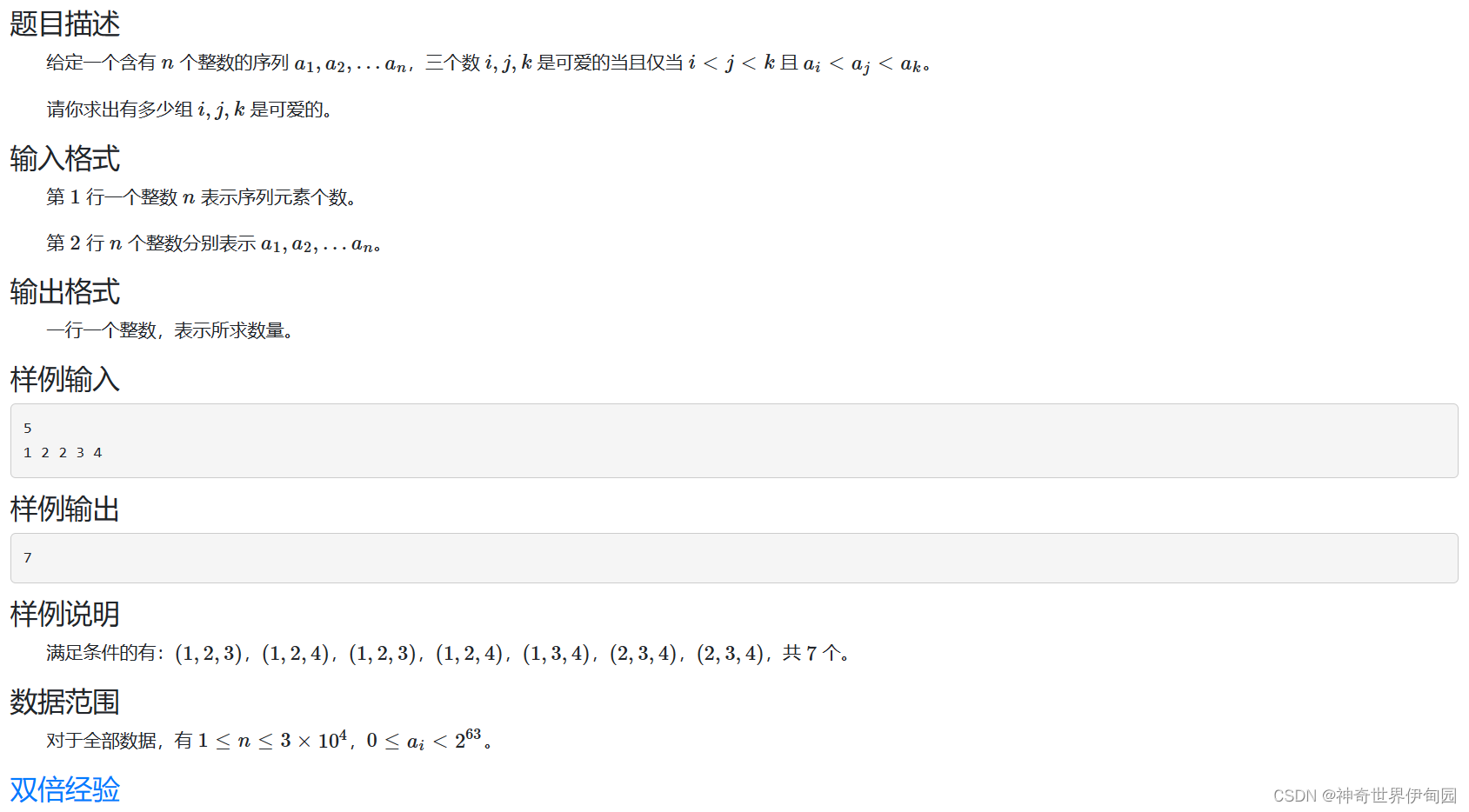
可以通过暴力的算法枚举三个数出现的位置,但不一定要用三重循环, 枚举一个中间点,找比它小的点和比它大的点,然后找到个数做乘积,时间复杂度O(n2),这样比三重循环要好,三元组类型的题都可以这样写。
#include
#define int long long
using namespace std;
const int MX = 3E4+5;
int arr[MX];
int n, ans;
signed main()
{ios::sync_with_stdio(0);cin.tie(0);cin >> n;for(int i = 1; i <=n ; ++i){cin >> arr[i];}for(int m = 2; m < n; ++m){int cl=0, cr=0;for(int l = 1; l < m; ++l){if(arr[l] < arr[m]){cl++;}}for(int r = m+1; r <= n; ++r){if(arr[r] > arr[m]){cr++;}}ans += cl*cr;}cout << ans << endl;return 0;
} 本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!