南宁周赛13周
第一题
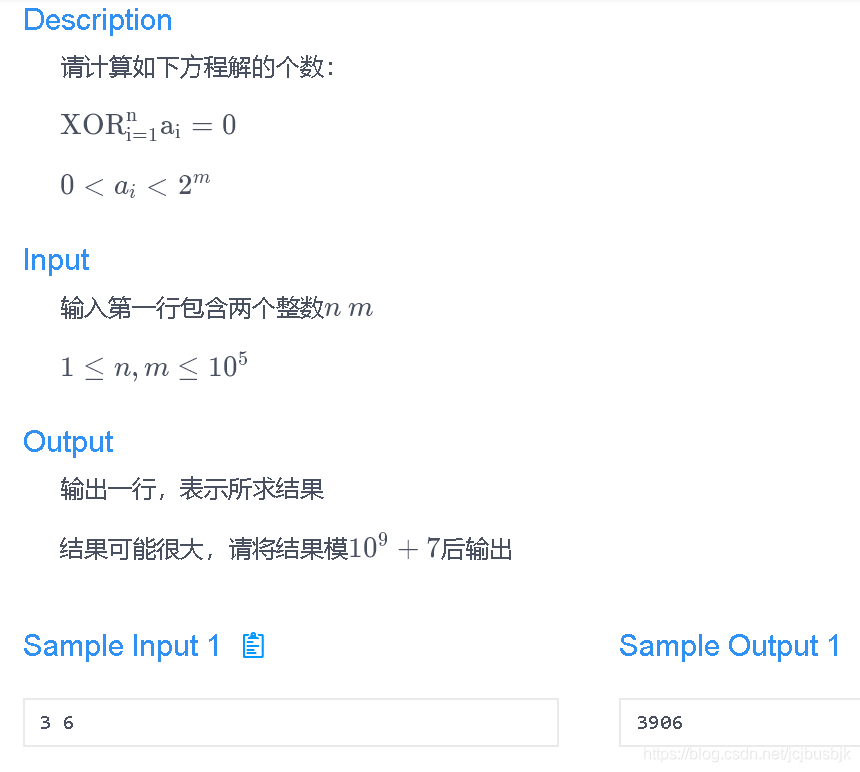
异或操作:
- 相同为0,不同为1
- 用1异或x能够使得x在0和1之间转换
- 偶数个相同的数异或在一起等于0
本题思路:本题是一个计数DP,突破口在于,当新的数加进来时,他的可能的值的数量与前面几个数异或的结果,以及他本身的取值范围有关。
新的数加进来后异或结果为0:前几个数异或结果为0了,由于新的数不为0,因此不可能。
前几个数异或结果不为0了,那么对于每一个结果,在范围内总能找到一个数与之中和得0。
新的数加进来后异或结果不为0:前几个数异或结果为0了,那么就有2m-1种方式使得结果不为0.
前几个数异或结果不为0:那么一定有一种方式是异或结果为0的,其余方式异或结果还是不为0,即2m-2种方式使得结果不为0.
个人见解,本题巧妙之处在于,将结果分成了两类,结果为0和结果不为0,作为一维状态,进行交替转换。
代码如下:
【在代码中,值得注意的是,2m求的时候会太大,因此要一个个%mod慢慢求】
#include第四题

这道题和上一题类似,改变的是每一个数拥有了自己的数据范围,根据上题的经验,异或运算是方便计数转化的,这题我们不难想到也是用计数DP。由于b的数据范围一直在变化,我们不难想到可能要特意写一个循环给整个异或进行到的位数。
还应该写一个循环给进行到第几个数。
进行到每个数的时候,需要存储当前位的值,以及当前数有没有使得当前位发生变化。
当当前数当前位为0的计数:当前位之后的数的选择乘上上一个数状态同样状态的计数。(因为0异或0,1都是其本身)
当当前数当前位为1的计数:
如果前几个数的当前位异或是1,则当当前值决策不会产生当前位的变化时,当前值异或1,其余和为0的计数一样。
当当前值决策会产生当前值的变化的时候,除了本来就得到答案的计数,还有每一位未改变得到这个答案的计数,和每一位改变了得到这个答案的计数乘以可以改变的数量,也就是后面位数随机组合的数量260-k.
没有变化的时候,所有数异或起来为0,则基础值为1,否则基础值为0.最后统计变化后所有位都为0的情况。
代码如下:
#include//统计初始值是不是就异或为0了if(t==0)res=1;elseres=0;for(ll d=60;d>=0;d--){memset(dp,0,sizeof dp);dp[0][0][0]=1;t=1ll<<d;//表示在哪一位z=0; //表示有多少个1 for(ll i=1;i<=n;i++)//枚举每个数 {if(!(b[i]&t))//d位置为0{for(ll j=0;j<2;j++)for(ll k=0;k<2;k++){dp[i][j][k]=dp[i-1][j][k]*((b[i]+1)%mod)%mod;//有每种数再加第k位一种数的情况 }} else{z++; for(ll j=0;j<2;j++){dp[i][j][0]=dp[i-1][j^1][0]*(((b[i]^t)+1)%mod)%mod;dp[i][j][1]=((dp[i-1][j^1][1]*(((b[i]^t)+1)%mod)%mod+dp[i-1][j][0]%mod)%mod+dp[i-1][j][1]*t%mod)%mod;//要一个个取模不然会溢出的!!!这就是标程为什么分开来取模!!! }b[i]^=t;//改变该位情况 }}res=(res+dp[n][0][1]%mod)%mod;//cout<if(z&1) break;//奇数的话就不用做了。 }cout<<res;return 0;
}
第二题

这还是一道卡时间的题目。一开始我用线性筛素数加公式法,
即 n ! = ∏ p r i m e s [ i ] n!=\prod_{}primes[i] n!=∏primes[i]n/i
但是最后大数还是过不去不知道哪里出了问题
代码如下:
include<iostream>
#includell n;while(cin>>n){if(n==0){cout<<"0"<<endl;}else{ll m=0,res=1;while(primes[m]<=n&&primes[m]!=-1){ll power=call(primes[m],n)%mod;res*=quickpow(primes[m],power)%mod;m++;}cout<<res%mod<<endl;}}return 0;
}
后来我发现竟然是个打表题。。。好吧也不是很惊讶,自己当时的思维不是很活跃,早就该想到的。。。
106的倍数都打在表里即可。
下面是打表代码:
#include然后下面是题解:
#include第三题

这道题曾经有一个106规模的类似的题,我们无论是运用筛约数也好,用约数个数公式也好,都很容易做出来。
约数个数和公式: ∑ k = 1 n n i \sum_{k=1}^{n}\frac{n}{i} k=1∑nin
但是对于109来说这远远不够。
下面我们来看整数分块问题:
这个在数论中运用很普遍,例如莫比乌斯反演。
并且最经典的应用就是在对 n i \frac{n}{i} in求和上。
假设n为10.
n/1=1;
n/2=5;
n/3=3;
n/4=2;
n/5=2;
n/6=1;
n/7=1;
n/8=1;
n/9=1;
n/10=1;
我们可以看到,除4和除5结果相同,除678910结果都相同,我们便不需要一个个把结果相加。我们把除出来结果相同的分为一个块【n/i,n/(n/i)】。
此时,每一个块的结果都是n/i,将n/i乘上n/(n/i)-n/i+1,相当于一次性加起来了,大大降低了复杂度。在这里我们只需O( x 2 \sqrt{x^2} x2)的时间复杂度求出约数个数和。
代码如下:
#include本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!