【2021年蓝桥杯Java-B组省赛（第一场）题解】

2021Java-B组省赛（第一场）

• • • 一、ASC
    • 二、卡片（模拟）
    • ※三、直线（模拟）
    • 四、货物摆放（约数）
    • 五、路径（最短路径）
    • 六、时间显示（模拟）
    • 七、最少砝码（找规律）
    • 八、杨辉三角形
    • 九、双向排序
    • 十、括号序列

一、ASC

已知大写字母 A 的 ASCII 码为 65，请问大写字母 L 的 ASCII 码是多少？

public class Main {public static void main(String[] args) {System.out.println((int)('L'));}
}

答案：76

二、卡片（模拟）

小蓝有很多数字卡片，每张卡片上都是数字 0 到 9。小蓝准备用这些卡片来拼一些数，他想从 1 开始拼出正整数，每拼一个，就保存起来，卡片就不能用来拼其它数了。
小蓝想知道自己能从 1 拼到多少。例如，当小蓝有 30 张卡片，其中 0 到 9 各 3 张，则小蓝可以拼出 1 到 10，但是拼 11 时卡片 1 已经只有一张了，不够拼出 11。现在小蓝手里有 0 到 9 的卡片各 2021 张，共 20210 张，请问小蓝可以从 1 拼到多少？

public class Main {public static void main(String[] args) {int[] nums = new int[10];int flag = 0;for (int i = 1; i <= 20210; i++) {int tmp = i;while (tmp != 0) {nums[tmp % 10]++;if (nums[tmp % 10] > 2021) {System.out.println(i);System.out.println(tmp % 10);flag = 1;break;}tmp /= 10;}if (flag == 1) {break;}}}
}

不要想复杂了，从1开始统计每位数个数就行。
答案：3181

※三、直线（模拟）

在平面直角坐标系中，两点可以确定一条直线。如果有多点在一条直线上，那么这些点中任意两点确定的直线是同一条。

给定平面上 2 × 3 个整点 {(x,y)|0 ≤ x < 2,0 ≤ y < 3, x ∈ Z,y ∈ Z}，即横坐标是 0 到 1 (包含 0 和 1) 之间的整数、纵坐标是 0 到 2 (包含 0 和 2) 之间的整数的点。这些点一共确定了 11 条不同的直线。

给定平面上 20 × 21 个整点 {(x,y)|0 ≤ x < 20,0 ≤ y < 21, x ∈ Z,y ∈ Z}，即横坐标是 0 到 19 (包含 0 和 19) 之间的整数、纵坐标是 0 到 20 (包含 0 和 20) 之间的整数的点。请问这些点一共确定了多少条不同的直线。

这道题属实不会做啊…一开始在找规律，发现找不到规律呀！

那就遍历！遍历每两个点，找到k、b，然后去重。注意，因为k、b可能为分数，最好的方式是转换成String，存入Map！！！

// 存储每一个坐标
class node {int x, y;node (int x, int y) {this.x = x;this.y = y;}
}
public class Main {public static void main(String[] args) {Scanner scan = new Scanner(System.in);int x = scan.nextInt();int y = scan.nextInt();node[] nodes = new node[500];int index = 0;for (int i = 0; i < x; i++) {for (int j = 0; j < y; j++) {// 存储每一个坐标nodes[index++] = new node(i, j);}}HashSet<String> set = new HashSet<>();// 遍历每两个点for (int i = 0; i < index; i++) {int x1 = nodes[i].x;int y1 = nodes[i].y;for (int j = i + 1; j < index; j++) {// y = kx + bint x2 = nodes[j].x;int y2 = nodes[j].y;String ans = "";if (x2 == x1) {ans = "x=" + x2;} else {if (y2 == y1) {ans = "y=" + y2;} else {int a = y2 - y1;int b = x2 - x1;int tmp = gcd(Math.abs(a), Math.abs(b));// 约分a = a / tmp;b = b / tmp;if ((a > 0 && b > 0) || (a < 0 && b < 0)) {// 就取x1,y1算ba = Math.abs(a);b = Math.abs(b);int up = y1 * b - a * x1;int down = b;int tmpp = gcd(Math.abs(up), Math.abs(down));up = up / tmpp;down = down / tmpp;if (up == 0) {// y = kxans = "y=" + a + "/" + b + "x";} else if ((up > 0 && down > 0) || (up < 0 && down < 0)) {up = Math.abs(up);down = Math.abs(down);ans = "y=" + a + "/" + b + "x" + "+" + up + "/" + down;} else if ((up > 0 && down < 0) || (up < 0 && down > 0)) {up = Math.abs(up);down = Math.abs(down);ans = "y=" + a + "/" + b + "x" + "+" + "-" + up + "/" + down;}} else if ((a < 0 && b > 0) || (a > 0 && b < 0)) {a = Math.abs(a);b = Math.abs(b);// 就取x1,y1算bint up = y1 * b - a * x1;int down = b;int tmpp = gcd(Math.abs(up), Math.abs(down));up = up / tmpp;down = down / tmpp;if (up == 0) {// y = kxans = "y=" + "-" + a + "/" + b + "x";} else if ((up > 0 && down > 0) || (up < 0 && down < 0)) {up = Math.abs(up);down = Math.abs(down);ans = "y=" + "-" + a + "/" + b + "x" + "+" + up + "/" + down;} else if ((up > 0 && down < 0) || (up < 0 && down > 0)) {up = Math.abs(up);down = Math.abs(down);ans = "y=" + "-" + a + "/" + b + "x" + "+" + "-" + up + "/" + down;}}}}System.out.println(ans);set.add(ans);}}System.out.println(set.size());}static int gcd (int a, int b) {if (b == 0) return a;return gcd(b, a % b);}
}

使用gcd约分时，不用管分子分母的正负，把分子分母/gcd后约分的结果会考虑正负的。例如gcd(-4,-2) = -2，-4 / -2 = 2 / 1，与除以-2约分是一样的，所以就不用再判断分子、分母正负了。

上面的代码自己做复杂了，太蠢了…

直接用：(y1-y2) * x +(x2-x1) * y +( x1 * y2 - x2 * y1)=0直线方程（由两点式转换而来），这种方程避免了精度问题，也避免了分数表达问题，只需要对三个数求gcd进行约分，太妙了！自己没有想到，高中知识忘完了。

答案：40257

四、货物摆放（约数）

小蓝有一个超大的仓库，可以摆放很多货物。

现在，小蓝有 n 箱货物要摆放在仓库，每箱货物都是规则的正方体。小蓝规定了长、宽、高三个互相垂直的方向，每箱货物的边都必须严格平行于长、 宽、高。

小蓝希望所有的货物最终摆成一个大的立方体。即在长、宽、高的方向上分别堆 L、W、H 的货物，满足 n = L × W × H。

给定 n，请问有多少种堆放货物的方案满足要求。 例如，当 n = 4 时，有以下 6 种方案：1×1×4、1×2×2、1×4×1、2×1×2、 2×2×1、4×1×1。

请问，当 n = 2021041820210418 （注意有 16 位数字）时，总共有多少种方案？

这道题当时也不会做，因为上一道题没想出来就很焦虑…然后又遇到这道题，更焦虑了…整个比赛一直在焦虑…

    // 4 有 3个约数：1 2 4// 最外面可以提供 3 种，最中间可以提供 3 种，6种// 6：1 2 3 6// 1 6 提供 三种，2 3 提供三种，6种// 找约数的个数，如果能被2整除 = 约数个数 / 2 * 3// 不能被2整除 = (约数个数 / 2 + 1) * 3// 这规律不就出来了	

上面的规律是错的…只考虑了两个约数组合，没有考虑三个、多个约数组合！！！先求出所有约数，然后三重循环，积=n即可。 找约数用sqrt!!!

public class Main {public static void main(String[] args) {// 问题转换为快速找一个 大数 的约数// 注意java的long要在后面加L！！！long num = 2021041820210418L;int index = 0;long[] divisor = new long[100000];for (long i = 1; i <= (long)Math.sqrt(num); i++) {if (num % i == 0) {divisor[index++] = i;if (i * i != num) {divisor[index++] = num / i;}}}int res = 0;// 顺序改变也算不同方案for (int i = 0; i < index; i++) {for (int j = 0; j < index; j++) {for (int k = 0; k < index; k++) {if (divisor[i] * divisor[j] * divisor[k] == num) {res++;}}}}System.out.println(res);}
}

答案：2430

前面的题目说实话都不难，靠模拟就能得到答案，都做对了，再加上后面几道简单的编程题，随随便便就省一了（四川省）。但是比赛场上，真的遇到需要多思考的题目难以静下心去思考，容易烦躁、焦虑，总想着题目都是一看就做得来的，那肯定是不可能的，比赛的时候一定要保持好良好的心态，仔细+心态要稳，一定要稳住，仔细读题，仔细分析，多多磨练自己比赛的心态…

五、路径（最短路径）

小蓝学习了最短路径之后特别高兴，他定义了一个特别的图，希望找到图 中的最短路径。

小蓝的图由 2021 个结点组成，依次编号 1 至 2021。

对于两个不同的结点 a, b，如果 a 和 b 的差的绝对值大于 21，则两个结点 之间没有边相连；如果 a 和 b 的差的绝对值小于等于 21，则两个点之间有一条 长度为 a 和 b 的最小公倍数的无向边相连。

例如：结点 1 和结点 23 之间没有边相连；结点 3 和结点 24 之间有一条无 向边，长度为 24；结点 15 和结点 25 之间有一条无向边，长度为 75。

请计算，结点 1 和结点 2021 之间的最短路径长度是多少。

数据结构方面的题目还没刷，待更，（树、图）

学成归来！！就是简单的最短路径模板题，这里用SPFA，因为可以处理负环，我给大家表演打板子。

public class main {public static void main(String args[]) {// 编号1 - 2021List<int[]>[] graph = new LinkedList[2022];for (int i = 0; i < 2022; i++) {graph[i] = new LinkedList<>();}// 建图for (int i = 1; i <= 2021; i++) {for (int j = i + 1; j <= 2021; j++) {// 无向边：双向if (Math.abs(i - j) > 21) continue;graph[i].add(new int[] {j, i * j / gcd(i, j)});graph[j].add(new int[] {i, i * j / gcd(i, j)});}}// SPFA// 记录答案int[] distTo = new int[2022];Arrays.fill(distTo, Integer.MAX_VALUE);// 起点距离 = 0distTo[1] = 0;// 是否在队列中boolean[] vis = new boolean[2022];// 起点入队vis[1] = true;Queue<Integer> queue = new LinkedList<>();queue.offer(1);while (!queue.isEmpty()) {int curId = queue.poll();// 出队vis[curId] = false;// 遍历相邻节点for (int[] node : graph[curId]) {int to = node[0];int weight = node[1];// 可以更新if (distTo[to] > weight + distTo[curId]) {distTo[to] = weight + distTo[curId];if (vis[to] == false) {// 入队vis[to] = true;queue.offer(to);}}}}System.out.println(distTo[2021]);}static int gcd(int a, int b) {return b == 0 ? a : gcd (b, a % b);}
}

答案：10266837

六、时间显示（模拟）

注意ms转s是1000，直接算。

import java.util.*;public class Main {public static void main(String[] args) {// 10^18Scanner scan = new Scanner(System.in);long n = scan.nextLong();// ms => sn = n / 1000;long hour = n / 60 / 60 % 24;long min = n / 60 % 60;long sec = n % 60;System.out.printf("%02d:%02d:%02d", hour, min, sec);}
}

七、最少砝码（找规律）

我们先看看C++组的砝码称重：


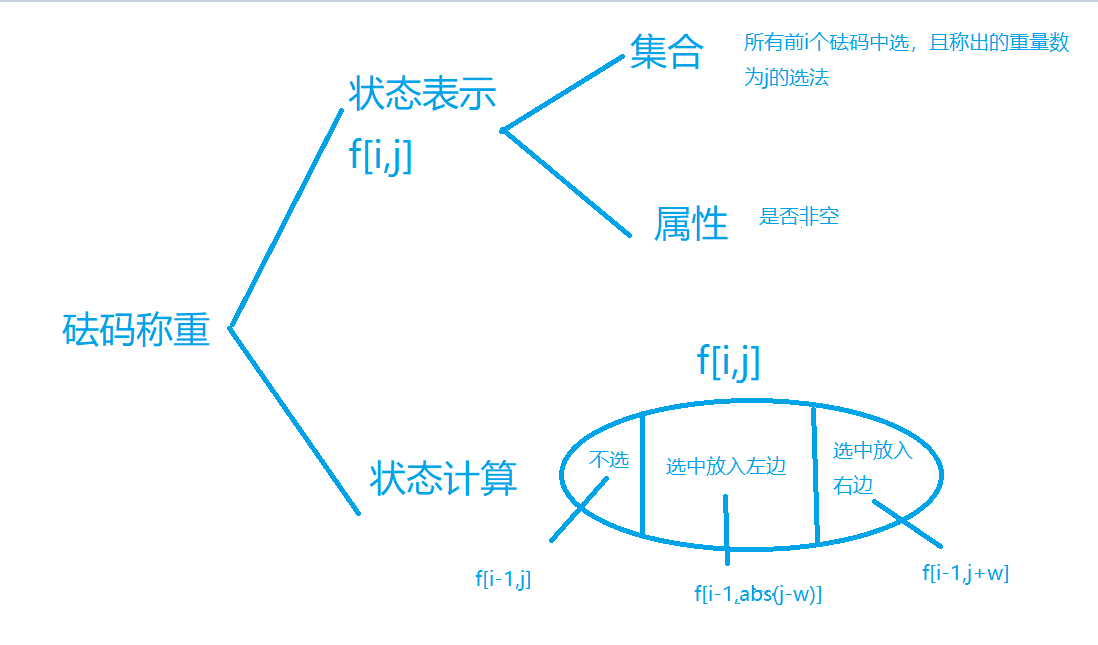
对于一个砝码，把它放在左边算+，放在右边算-，不放算0，现在有N个砝码，可以看成背包问题，dp[i][j]：只从前 i 个物品中选，且总重量为 j 的所有方案的集合，那么dp[i][j]的属性值应该表示这个集合是否为非空（boolean）。最后再枚举所有砝码的总重，如果dp[i][j]非空，那就是凑出了新的正整数，答案就+1。

import java.util.*;public class Main {public static void main(String[] args) {Scanner scan = new Scanner(System.in);int n = scan.nextInt();int[] w = new int[101];// 砝码总重int m = 0;for (int i = 1; i <= n; i++) {w[i] = scan.nextInt();m += w[i];}boolean[][] dp = new boolean[101][200010];// dp[i][j]：只考虑前 i个砝码，能否凑出正整数 j// -100000 <= j <= 100000// 负数不能表示，可以加上偏移// 0 <= j <= 200000// 一个砝码放左边是 + ，放右边是 -，不放是0// 偏移量int B = 200010 / 2;// 0个砝码可以凑出0 + B（偏移）dp[0][B] = true;for (int i = 1; i <= n; i++) {for (int j = -m; j <= m; j++) {// 遍历三种情况：不放、放左边、放右边dp[i][j + B] = dp[i - 1][j + B];if (j - w[i] >= -m) {dp[i][j + B] |= dp[i - 1][j - w[i] + B];}if (j + w[i] <= m) {dp[i][j + B] |= dp[i - 1][j + w[i] + B];}}}// 注意偏移量一定要都加上int ans = 0;// 最大的情况就是砝码总重for (int i = 1; i <= m; i++) {if (dp[n][i + B]) {ans++;}}System.out.println(ans);}
}

回到java组的这道题，并不是dp，而是找规律。（根本想不到…）

只需要找到第一个total >= n的count即可。

public class Main {public static void main(String[] args) {Scanner sc = new Scanner(System.in);int n = sc.nextInt();int weight = 1;int count = 1;int total = 1;while (total < n) {count++;weight *= 3;total += weight;}System.out.println(count);}
}

八、杨辉三角形

因为只用找第一次出现的数字，只需要关注杨辉三角的左半边

1
1 2
1 3
1 4 6
1 5 10

而每一行的第一个元素 = 1 * 行数 / 1，第二个元素 = 第一个元素 * （行数-1）/ 2，这里的行数从0开始算才成立。

#include 
typedef long long ll;
using namespace std;
ll N;
ll C(int a, int b)//求第i行第j列的值
{ll res = 1;for (ll i = a, j = 1; j <= b; i--, j++){res = res * i / j;if (res > N)//如果中间结果超过N就直接返回return res;}return res;
}
int main()
{cin >> N;for (int k = 16; k >= 0; k--)//一列一列的找{ll l = 2 * k, r = max(N, l), mid;while (l <= r) {//对第k列二分查找行mid = l + (r - l) / 2;//二分行ll CC = C(mid, k);if (CC == N)break;else if (CC > N)r = mid - 1;elsel = mid + 1;}if (C(mid, k) == N){//第mid行、第k列的数就是Ncout << (mid + 1) * mid / 2 + k + 1 << endl;//杨辉三角形的行数符号公差为1的等差数列，故用等差数列求和公式//加上第几列再加上1（因为列从0开始）即可得出该数的位置break;}}return 0;
}

转自：https://blog.csdn.net/zjsru_Beginner/article/details/121875334

九、双向排序

只会暴力骗分…贴一个yxc大佬写的：

#include 
#include 
#include #define x first
#define y secondusing namespace std;typedef pair<int, int> PII;const int N = 100010;int n, m;
PII stk[N];
int ans[N];int main()
{scanf("%d%d", &n, &m);int top = 0;while (m -- ){int p, q;scanf("%d%d", &p, &q);if (!p)//操作1 {while (top && stk[top].x == 0) q = max(q, stk[top -- ].y);//出现连续的操作1，我们取最大 while (top >= 2 && stk[top - 1].y <= q) //如果当前的操作1比上一次的操作1范围大，则将上一次操作1和操作2删除 top -= 2;stk[ ++ top] = {0, q};//存本次最佳操作 }else if (top)//操作2 &&且操作1已经进行过（操作二第一个用没效果） {while (top && stk[top].x == 1) q = min(q, stk[top -- ].y);while (top >= 2 && stk[top - 1].y >= q) top -= 2;stk[ ++ top] = {1, q};}}int k = n, l = 1, r = n;for (int i = 1; i <= top; i ++ ){if (stk[i].x == 0)//如果是操作1 while (r > stk[i].y && l <= r) ans[r -- ] = k -- ;//移动r值 ，并赋值 elsewhile (l < stk[i].y && l <= r) ans[l ++ ] = k -- ; if (l > r) break;}if (top % 2)while (l <= r) ans[l ++ ] = k -- ;elsewhile (l <= r) ans[r -- ] = k -- ;for (int i = 1; i <= n; i ++ )printf("%d ", ans[i]);return 0;
}

十、括号序列

是dp，但是推不出来转移方程…GG

这年题目好难…基本只能靠填空题和前面的编程题…

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！