P, NP, NP-Complete, NP-Hard 问题

P, NP, NP-Complete, NP-Hard 问题

形如： a x n + b x n − 1 + ⋯ + c ax^n+bx^{n-1}+\cdots+c axn+bxn−1+⋯+c 这种形式的式子称为 $x$ 的 $n$ 次多项式。一个算法的时间复杂度可以分为多项式时间复杂度和非多项式时间复杂度，多项式时间复杂度由小到大依次为： O ( 1 ) ＜ O ( l o g n ) ＜ O ( n ) ＜ O ( n l o g n ) ＜ O ( n 2 ) ＜ O ( n 3 ) Ο(1)＜Ο(logn)＜Ο(n)＜Ο(nlogn)＜Ο(n^2)＜Ο(n^3) O(1)＜O(logn)＜O(n)＜O(nlogn)＜O(n2)＜O(n3) ，非多项式时间复杂度由小到大依次为： O ( 2 n ) ＜ O ( n ! ) ＜ O ( n n ) Ο(2^n)＜Ο(n!)＜Ο(n^n) O(2n)＜O(n!)＜O(nn) ，非多项式时间复杂度大于多项式时间复杂度。

P问题（Polynominal）：即可以在多项式时间内解决的问题。一个规模为 $n$ 的问题，如果能在 $n$ 的多项式时间内解决，就是P问题。

NP问题（Non-deterministic Polynominal，非确定性多项式）：即能够在一个多项式时间里验证一个解是否正确的问题。注意：求解与验证的时间复杂度是完全不同的，例如旅行家推销问题（TSP），找出一个路径长度小于 $L$ 且包含所有 $n$ 个城市的环路。如果是 ”求解“ 的话，时间复杂度将达到 $O(n!)$ ，但如果是 ”验证“ 一条环路是否符合要求，那时间复杂度就低得多了。所谓 ”非确定“ 是指我们不知道 NP问题 是否存在一个多项式时间复杂度的算法，也就是不确定它是不是一个 P问题。即 NP问题 是 P问题 的超集。

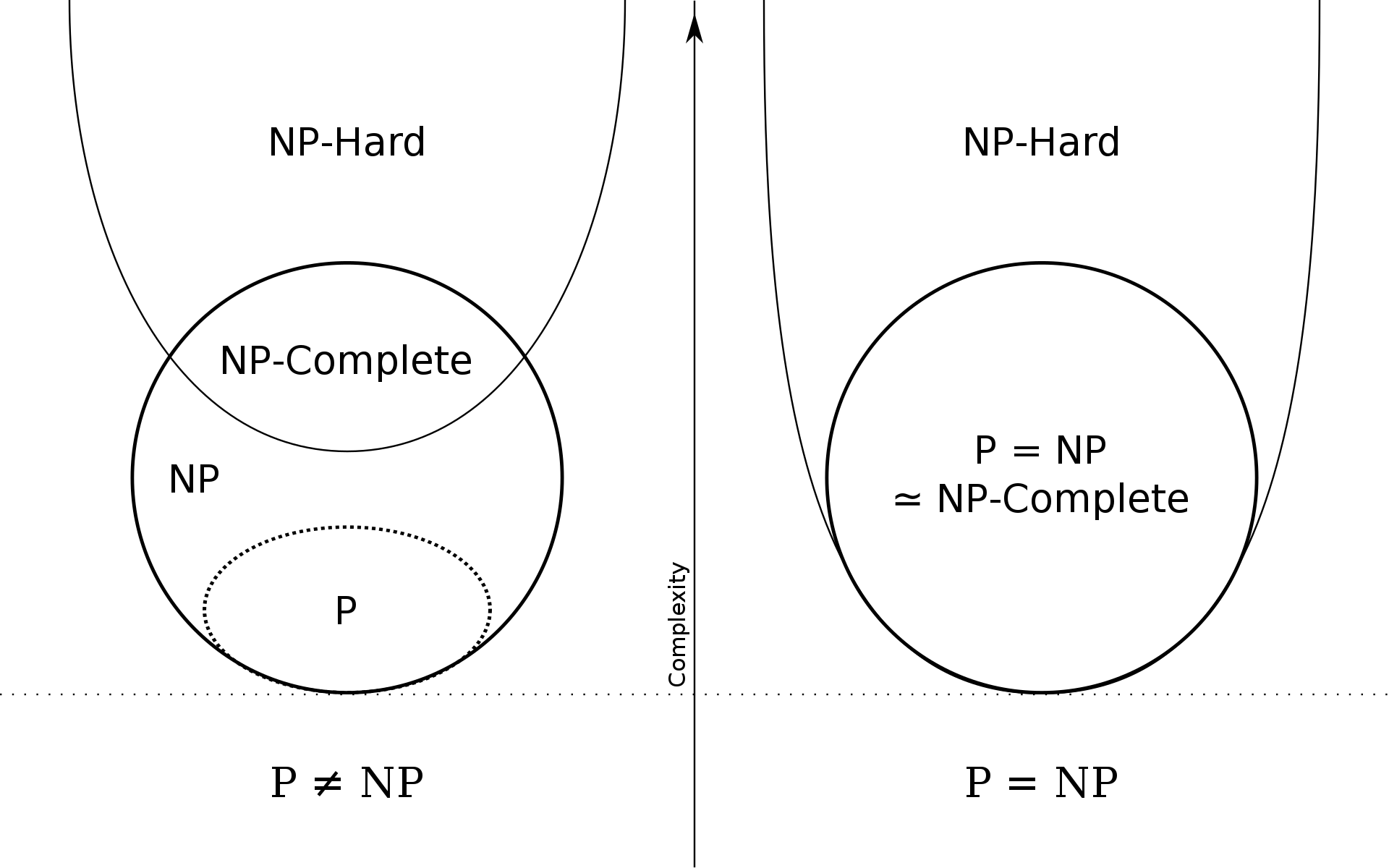
若所有的 NP问题 都能在多项式时间内归约到问题X（X的复杂度大于等于原 NP问题），那么X就是一个 NP-hard问题，如果X也是NP的，那么X是NP complete 的，否则 X 只能是 NP-Hard 的。

NP-Complete 问题（Non-determinism Polynomial Complete）：NP-complete 问题满足两个条件：①是一个NP问题 ②所有NP问题都可以约化到它

NP-Hard 问题：其满足所有的NP问题都可以约化到它，但其并不一定是一个 NP 问题。

参考资料：

1. P问题、NP问题、NP完全问题和NP难问题（知乎专栏）
2. P问题、NP问题、NP完全问题和NP难问题（CSDN）
3. 谈谈计算机中的NP，NP-Hard，NP完全以及"NP=P？"问题（哔哩哔哩）

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！