蓝桥杯之“砝码称重“解题思路，含图解（Java）

问题描述

你有一架天平和 N 个砝码，这 N 个砝码重量依次是 W_1, W_2, · · · , W_N。

请你计算一共可以称出多少种不同的重量？ 注意砝码可以放在天平两边。

输入格式

输入的第一行包含一个整数 N。

第二行包含 N 个整数：W_1, W_2, W_3, · · · , W_N​。

输出格式

输出一个整数代表答案。

样例输入

3
1 4 6

样例输出

10

样例说明

能称出的 10 种重量是：1、2、3、4、5、6、7、9、10、11

问题分析：

首先分析问题的类型，每一个砝码只能选择取或者不取，类似于01背包问题。

每一种不同重量都可以从计算上次秤出的重量中上得出，这句话可能大家没有太明白。

我这里解释一下，比如说：

假设砝码a，b，c的重量分别为1，4，6

一开始，天平上只有砝码a，天平上只有砝码a说明秤出的重量只有1。

此时我们可以不放砝码b，或者放砝码b

放入砝码b就会秤出重量5和3，即4+1=5和4-1=3，我们可以把5和3作为新的砝码，等放入下一个砝码时，就可以在原来秤出的重量上计算新的重量

不放入b，天平上还是原来的重量

算法图解：

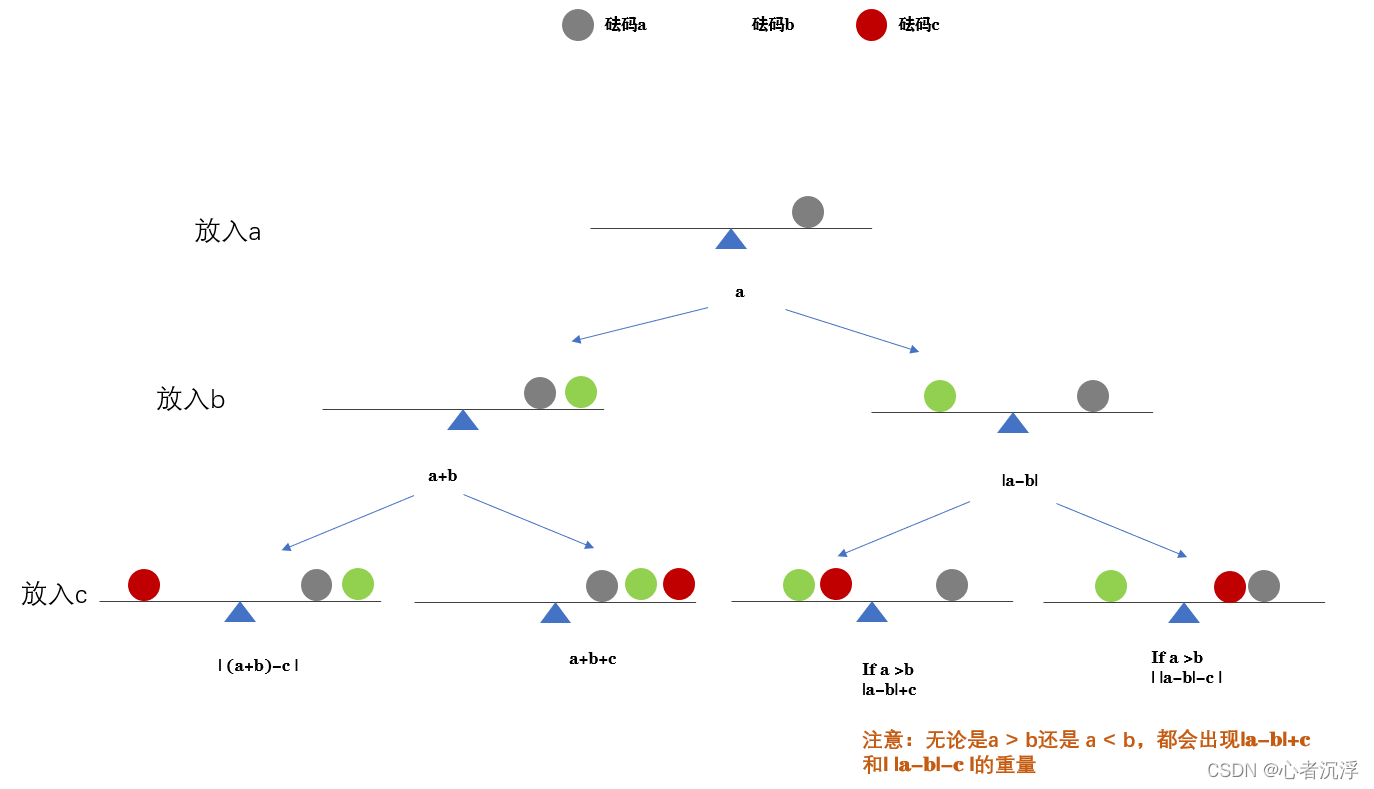
图解一：分析先放入a，再放入b，在放入c的图解

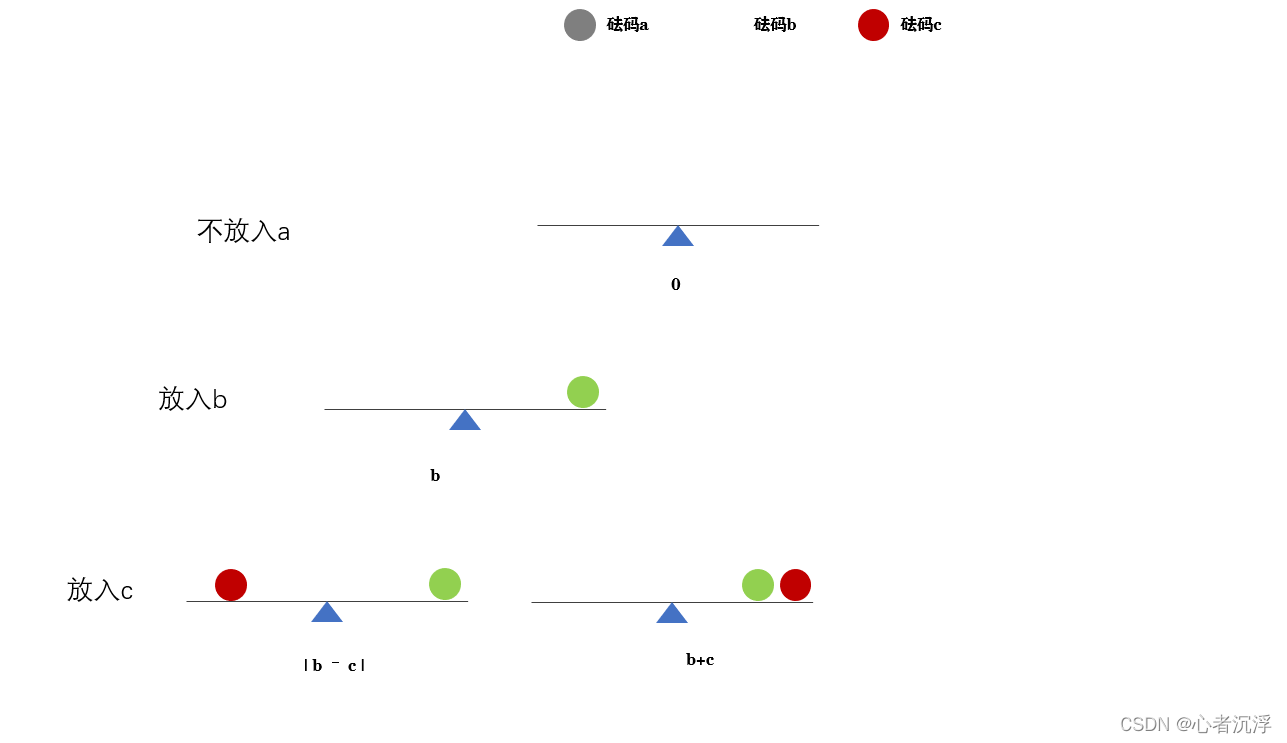
图解二：分析不放入a，再放入b，再放入c的情况

以上的图解只分析了两种情况 ，所有需要画出所有的情况，就会画出一颗树。

左子树代表选择放入新的砝码，右子树表示不放入新的砝码，也就是继承上次的重量。

注意：左子树可能会秤出两种重量

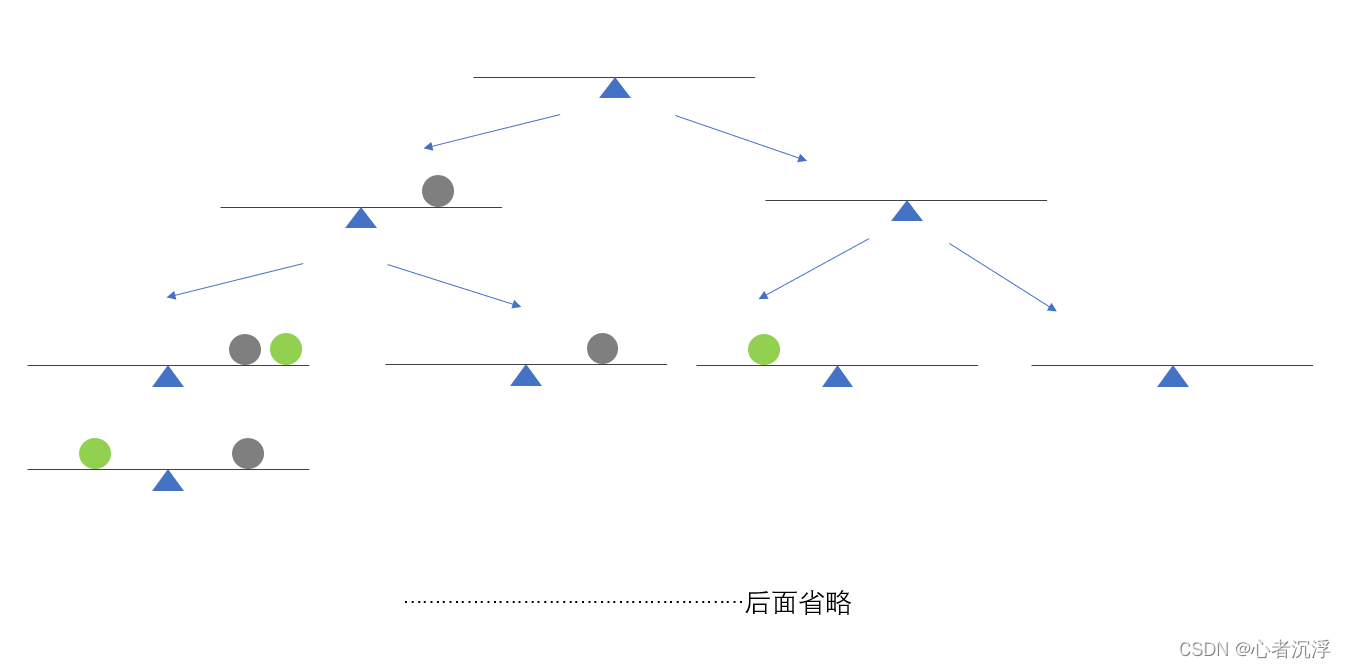
根据以上图解我们可以得出，每次放入新的砝码，都可以从上一次秤得的重量中计算得出。

完整代码如下：

import java.util.*;public class Main {public static void main(String[] args) {Scanner scan = new Scanner(System.in);Set set = new HashSet<>();int n = scan.nextInt();int[] fama = new int[n];for (int i = 0; i < n; i++) {fama[i] = scan.nextInt();}//初始化set,表示一开始天平上没有砝码，重量为0set.add(0);for (int i = 0; i < n; i++) {//在没放入新的砝码前，将秤得的所有重量放入list集合中List list = new ArrayList<>(set);for (int k : list) {//相加和相减取绝对值产生新的两个重量，并加重量放入set集合中//注意:如果新秤得的重量在原来的set集合存在，将不被放入set中set.add(k + fama[i]);set.add(Math.abs(k - fama[i]));}}//移除0元素set.remove((Object)0);//输出set集合大小，即秤得的重量数System.out.println(set.size());}
}

运行结果：

 当然了，本人也使用过递归爆搜的解法，由于利用暴力搜索的方法会产生大量的重复计算，

所以提交答案会提示超时，代码给有需要的读者作为参考：

import java.util.*;
// 1:无需package
// 2: 类名必须Main, 不可修改public class Main {public static void main(String[] args) {Scanner scan = new Scanner(System.in);Main main = new Main();Set result = new HashSet<>();int n = scan.nextInt();int[] fama = new int[n];for(int i = 0; i < n; i++){fama[i] =  scan.nextInt();}main.rese(0,fama,0,0,n,result);System.out.println(result.size());scan.close();}public void rese(int a,int[] fama,int sum1, int sum2,int n,Set result){if(sum1 - sum2 > 0){result.add(sum1 - sum2);}for(int i = a; i < n; i++){sum1 += fama[i];rese(i+1,fama,sum1,sum2,n,result);sum1 -= fama[i];sum2 += fama[i];rese(i+1,fama,sum1,sum2,n,result);sum2 -= fama[i];}}
}

 前些天发现了一个巨牛的人工智能学习网站，通俗易懂，风趣幽默，忍不住分享一下给大家

跳转到教程

finally，如果读者们可以理解我这个解法当然我是最开心的，虽然在表述上没这么清晰吧，但是图解是我的全部想法，这个解法也是我自己独立想出来的，感谢您的阅读！🏃

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！