第 106 场力扣夜喵双周赛

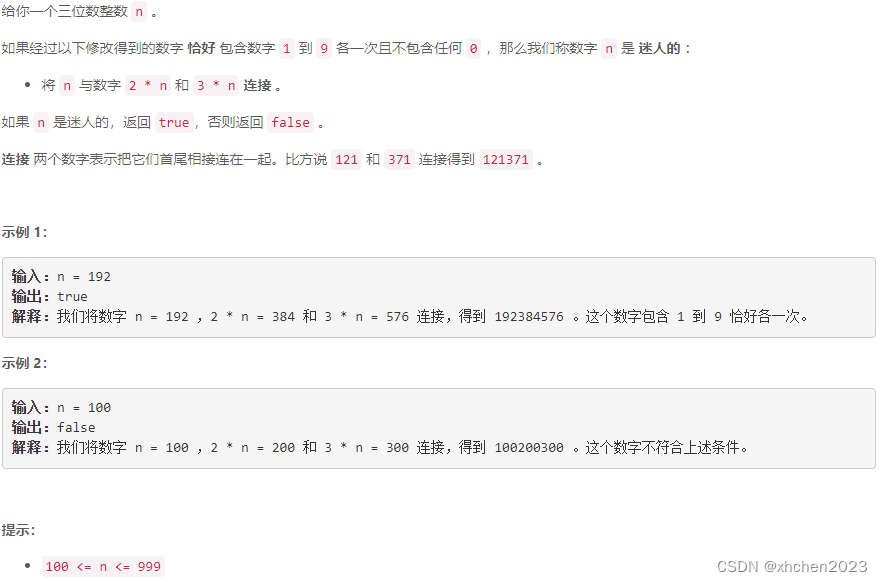
模拟: 拼接n, 2n, 3n, 排序后与’123456789’

class Solution {public:bool isFascinating(int n) {string s = to_string(n) + to_string(n * 2) + to_string(n * 3);sort(s.begin(), s.end());return s == "123456789";}
};

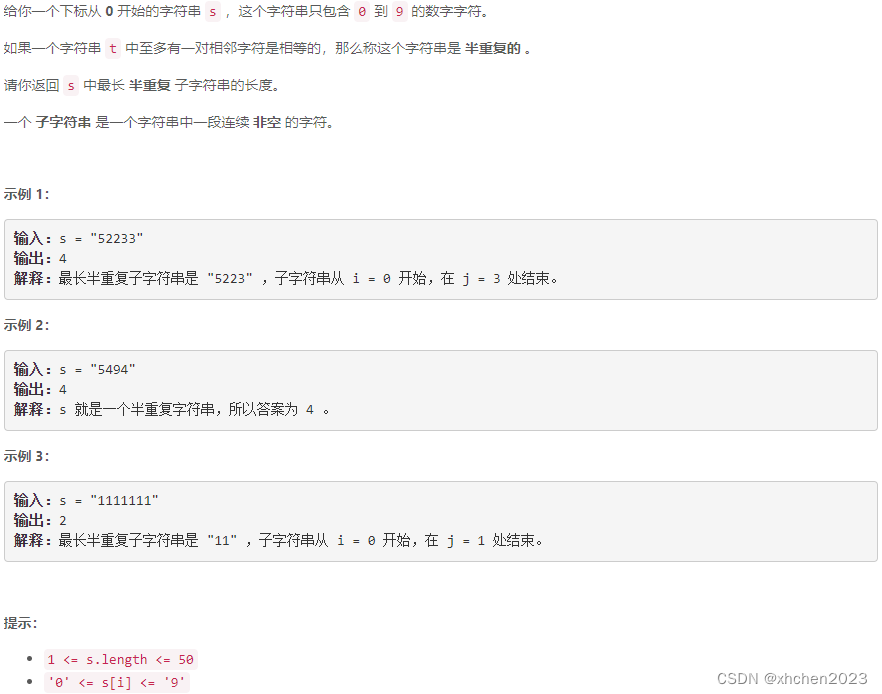
枚举: 数据范围小直接从大到小枚举子串…

class Solution {public:int longestSemiRepetitiveSubstring(string s) {int n = s.size();int res;for (int len = n;; len--) {for (int i = 0; i + len - 1 < n; i++) {int cnt = 0;for (int j = i; j < i + len - 1; j++)if (s[j] == s[j + 1])cnt++;if (cnt <= 1) return len;                }}}
};

脑筋急转弯: 如果不区分两个相撞的机器人, 则两个相撞的机器人之后各自反向等价于两个机器人互不影响始终朝各自最初方向移动, 所以可以求出经过d秒后所有机器人的位置, 之后排序+前缀和即可

class Solution {public:typedef long long ll;ll mod = 1e9 + 7;int sumDistance(vector<int>& nums, string s, int d) {int n = nums.size();vector<int> fin;for (int i = 0; i < n; i++)fin.push_back(s[i] == 'L' ? nums[i] - d : nums[i] + d);sort(fin.begin(), fin.end());ll res = 0, pre = fin[0];for (int i = 1; i < n; i++) {res += 1LL * fin[i] * i % mod - pre;res %= mod;pre += fin[i];}return (res % mod + mod) % mod;}
};

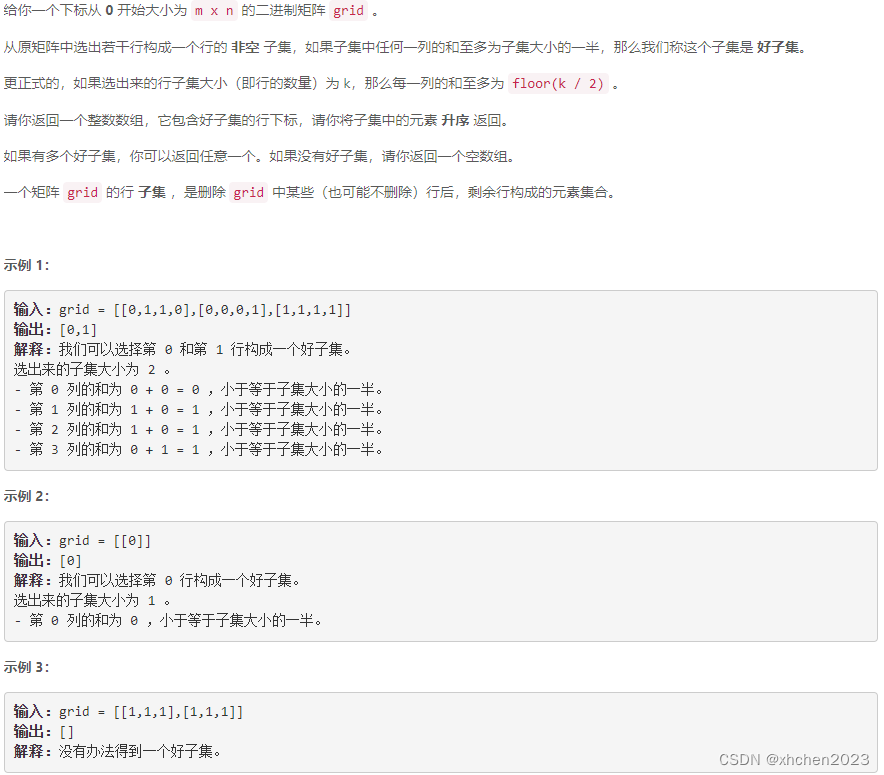
思维题: 可以证明在$1\le n\le 5$ 的前提下, 若存在大小大于2的好子集, 则一定存在大小为2的好子集. 所以按行遍历并维护已经出现过的行的1的状态集合 { m a s k i } \{mask_i\} {maski​}, 遍历到第j行时0的状态为 m a s k j mask_j maskj​, 遍历 m a s k j mask_j maskj​二进制子集, 若其中有在 { m a s k i } \{mask_i\} {maski​}出现过的, 则已经找到大小为2的好子集.

class Solution {public:vector<int> goodSubsetofBinaryMatrix(vector<vector<int>>& g) {int m = g.size(), n = g[0].size();vector<int> vis(1 << n, -1);for (int i = 0; i < m; i++) {int neg = 0, pos = 0;for (int j = 0; j < n; j++)if (g[i][j] == 1)pos |= 1 << j;elseneg |= 1 << j;if (!pos)return {i};for (int sub = neg; sub; sub = (sub - 1) & neg)//枚举neg的二进制子集if (vis[sub] != -1)//g[vis[sub]][x] & g[i][x] = 0 ,0 <= x < nreturn {vis[sub], i};vis[pos] = i;}return {};}
};