顺丰（顺丰鄂州枢纽运转中心环线检测）拓扑排序

【背景】
鄂州花湖机场是亚洲第一个、世界第四个专业货运枢纽机场。2016年4月获中国民用航空局正式批复，2017年12月20日枢纽工程正式开工，2022年3月19日由顺丰航空使用波音B757-200F型全货机执行试飞成功，系中国首次以全货机机型完成新机场的试飞工作。
顺丰鄂州枢纽转运中心占地约百万平方，实现了快件从卸载（卸车/卸机）到分拣再到装车/打板全自动化。自动化设备运输线总长超过数十公里。如何保障快件最高效到达装车或打板口是核心需要解决的问题。
转运中心内自动化设备通过运输线连接，构成一张立体的连通网络，快件达到分流路口需要决策行走支路，确保全程线路最优前提下，同时要避免大量快件涌向最短线路造成拥堵，还需要及时避开故障线路上的故障设备，直到故障得到修复。
自动化运输线简化图如下：

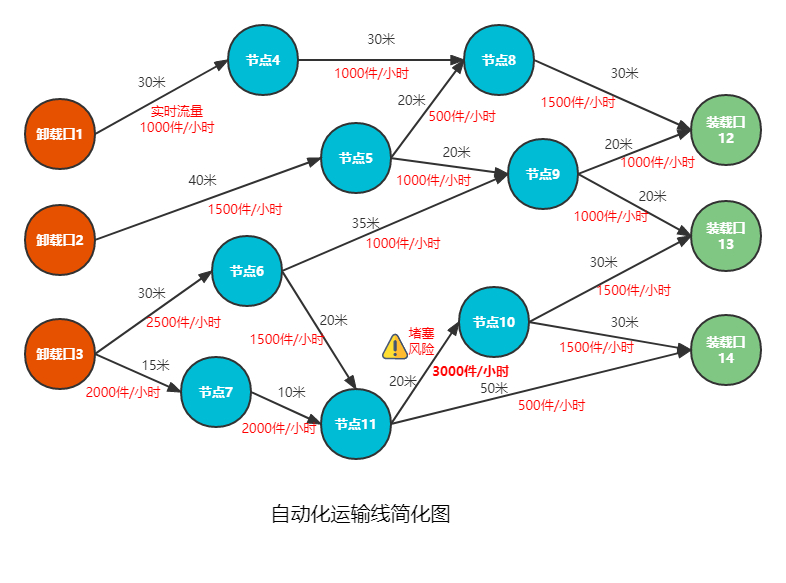
卸载口代表快件行走起始节点，装载口代表快件经过路线行走后最终目的节点，节点代表从卸载口到达装载口途径线路的分流或汇流点，卸载口和装载口也是一种特殊的节点。
边代表两个相邻节点间自动化设备运输线，线路代表从起始节点到达目的节点（装载口）途径所有的边。
在整连通网络上不应该存在环形线路，环形线路可能会导致快件在运输线上长时间运输，以至于错过飞机或车辆班次，导致延误。因此在建立线路数据模型时应避免出现环。

【问题】
请帮忙检测线路上是否存在环形通路。

示例 1：

输入：
"1->2,2->3,3->1"

输出：
true

示例 2：

输入：
"1->4,2->5,3->6,3->7,4->8,5->8,5->9,6->9,6->11,7->11,8->12,9->12,9->13,10->13,10->14,11->10,11->14"

输出：
false

示例 3：

输入：
"1->4,2->5,3->6,3->7,4->8,5->8,5->9,6->9,6->11,7->11,8->12,9->12,9->13,10->6,10->13,10->14,11->10,11->14"

输出：
true

解释:
存在环线:6->11,11->10,10->6

提示:

• 0 < 节点数 < 100

这一题看到图的问题，又看到了是否形成环，很自然的想到了用拓扑排序，首先要注意入读值表示的是有多少个节点指向该节点，还有就说划分字符串的时候要细心。 

class Solution {
public:bool hasCycle(string graph) {vector> nums;//存放所有的数组对find_nums(graph,nums);vector> check(max_val+1,vector(1,0));for(auto&k:nums)//数组中，第一个为入度值，应该是指向这个数的其他数的个数，其他项为临接值{check[k.first].push_back(k.second);check[k.second][0]++;}//把入度为0的值存放到队列中queue m_que;for(int i=1;i>& nums){int n=graph.size();int k=graph.find(",",0),ll=0;while(ll!=n)//拆分{string str=graph.substr(ll,k!=-1?k-ll:n-ll);int t1=str.find("-");string str1=str.substr(0,t1);str.erase(0,t1+2);int num1=stoi(str1),num2=stoi(str);nums.push_back(make_pair(num1,num2));ll=k==-1?n:k+1;k=graph.find(",",ll);max_val=max(max_val,num2);max_val=max(max_val,num1);}}int stoi(string str){int n=str.size(),ans=0;for(int i=0;i

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！