连珠线 题解

一、题目

二、分析

可知，每一组点形态有以下红蓝两种情况，

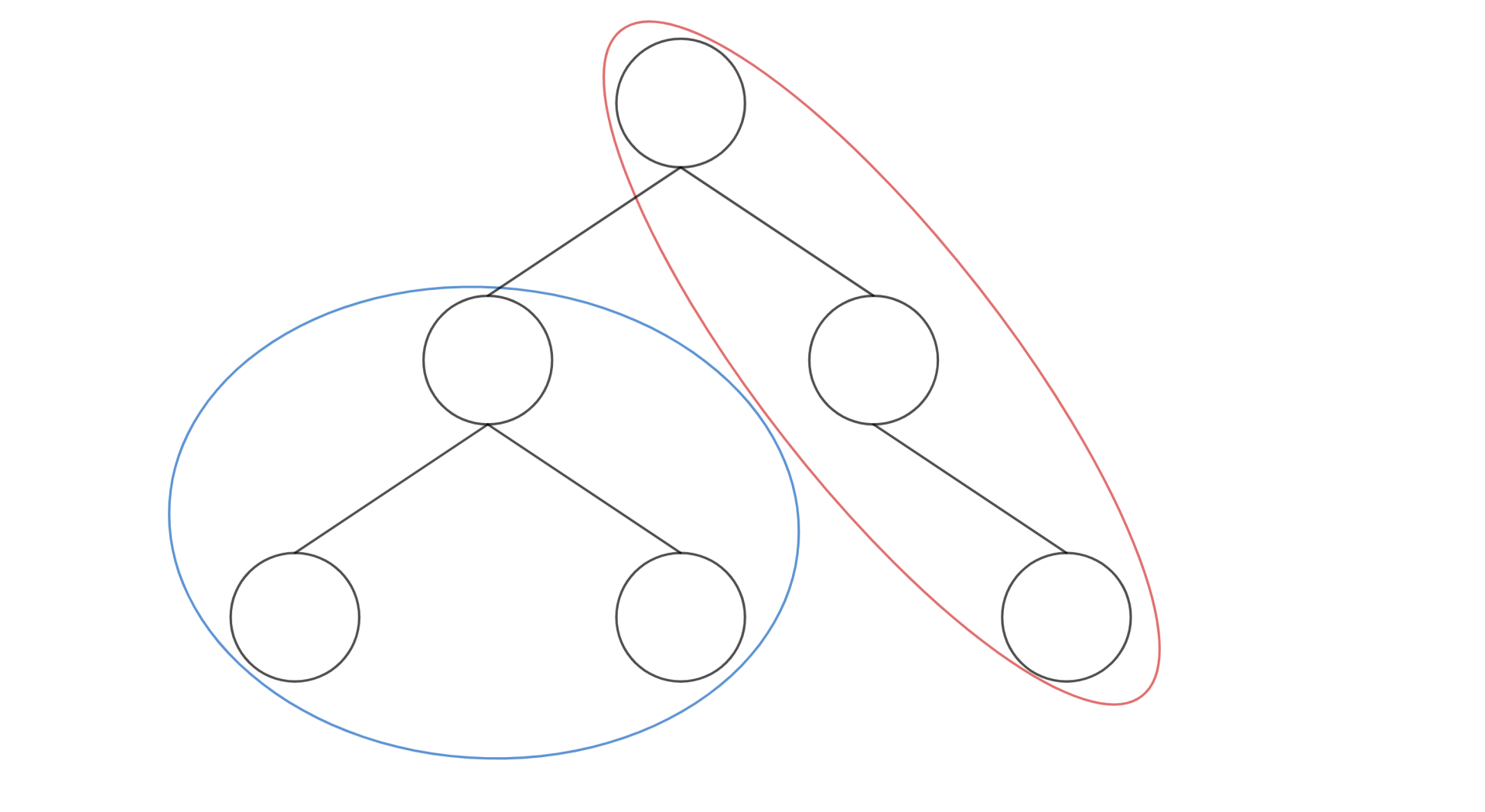
可以发现，若将根移动之后，蓝色圈情况可化为红色圈情况，其走向为 $son[x]-x-father[x]$ ；

所以考虑 换根DP ；

先考虑以一个节点为根如何计算答案；

则对于三点的中间点，由于其连接两条边，所以可以将其看作此组点的关键点；

所以定义状态 $dp[i][1/0]$ 表示以 $i$ 为根节点的子树中， $i$ 为 / 不为三点中点时答案最大值；

则枚举 $i$ 的子节点 $v$ ；

对于 $dp[i][0]$ ，则 $v$ 可为也可不为中点，所以有
d p [ i ] [ 0 ] = ∑ m a x { d p [ v ] [ 0 ] , d p [ v ] [ 1 ] + e [ i ] [ v ] } dp[i][0] = \sum{ max\{dp[v][0], \; dp[v][1] + e[i][v]\} } dp[i][0]=∑max{dp[v][0],dp[v][1]+e[i][v]}
对于 $dp[i][1]$ ，则应选择一个 $v$ ，使其与 $i$ 成为一组点中的两个，则其一定不能为中点，且一定选 $(i,v)$ 边；

则其转变后为 $dp[v][0]+e[i][v]$ ；

由于 $dp[i][1]$ 可包含 $dp[i][0]$ 所有情况，所以还要减去 $v$ 之前的贡献，即 m a x { d p [ v ] [ 0 ] , d p [ v ] [ 1 ] + e [ i ] [ v ] } max\{dp[v][0], \; dp[v][1] + e[i][v]\} max{dp[v][0],dp[v][1]+e[i][v]} ；

又由于 $i$ 只能为一组点的中点，所以选取变化后贡献最大的；

则有
d p [ i ] [ 1 ] = d p [ i ] [ 0 ] + max ⁡ { d p [ v ] [ 0 ] + e [ i ] [ v ] − m a x { d p [ v ] [ 0 ] , d p [ v ] [ 1 ] + e [ i ] [ v ] } } dp[i][1] = dp[i][0] + \max \{ dp[v][0] + e[i][v] - max\{dp[v][0], \; dp[v][1] + e[i][v]\} \} dp[i][1]=dp[i][0]+max{dp[v][0]+e[i][v]−max{dp[v][0],dp[v][1]+e[i][v]}}
由此可得定根下的答案；

考虑如何换根；

则对于跟节点 $i$ ，现要将根换到其子节点 $v$ ，则；

整棵树分为了两部分，对于根节点为 $v$ 的部分，其答案为 $dp[v][0]$ ；

对于其余部分，现已知以 $i$ 为根节点答案，

首先，因为根节点为 $v$ 的部分已独立出去了，所以应将其的贡献从以 $i$ 为根节点答案中减去；

定义数组 $dp1[i][1/0]$ 表示这部分中 $i$ 为 / 不为中点的答案，$dp2[i]$ 表示以 $i$ 为根节点的答案；

所以有
$$dp1[i][0]=dp2[i]-max(dp[v][0],dp[v][1]+e[i][v]);$$
以及
$$dp1[i][1]=dp1[i][0]+maxn[i];$$
其中， $maxn[i]$ 表示以 $i$ 为根节点的 m a x { d p [ v ] [ 0 ] , d p [ v ] [ 1 ] + e [ i ] [ v ] } } max\{dp[v][0], \; dp[v][1] + e[i][v]\} \} max{dp[v][0],dp[v][1]+e[i][v]}} ，在第一次 DP 时记录一下即可；

但注意，

有可能 $maxn[i]$ 所指节点刚好为要换到的根，则此时应用次大值来转移；

所以在第一次 DP 时应同时记录 m a x { d p [ v ] [ 0 ] , d p [ v ] [ 1 ] + e [ i ] [ v ] } } max\{dp[v][0], \; dp[v][1] + e[i][v]\} \} max{dp[v][0],dp[v][1]+e[i][v]}} 的最大与次大值；

在得到 $dp1$ 后，由于 $i$ 此时不再为根节点，所以其可以与其父节点 $fa$ 成为中点 （ $i$ 不为总根），或为原始中点；

所以同转移，其又会产生 $dp1[fa][0]+w[fa][i]-max(dp1[fa][0],dp1[fa][1]+w[fa][i])$ 的贡献；

将两种情况取最大值即可；

综上，有 $dp2[v]=dp[v][0]+max(dp1[i][0],dp1[i][1]+e[i][v])$ ；

最终在统计答案即可；

三、代码

#include 
#include 
#include 
#include 
using namespace std;
const int MAXN = 200005;
const int INF = 2147483647;
int n, a[MAXN];
int dp[MAXN][5], dp1[MAXN][5], dp2[MAXN], ans, vg[MAXN];
int maxn[MAXN], n_maxn[MAXN], pos[MAXN];
bool flag[MAXN];
struct edge {int to, tot;
};
vector  g[MAXN];
void dfs(int i) {flag[i] = true;maxn[i] = n_maxn[i] = -INF;int to;for (int t = 0; t < g[i].size(); t++) {int v = g[i][t].to, tot = g[i][t].tot;if (!flag[v]) {dfs(v);vg[v] = tot;dp[i][0] += max(dp[v][0], dp[v][1] + tot);to = dp[v][0] + tot - max(dp[v][0], dp[v][1] + tot);if (to > maxn[i]) n_maxn[i] = maxn[i], maxn[i] = to, pos[i] = v;else if (to > n_maxn[i]) n_maxn[i] = to;}}dp[i][1] = dp[i][0] + maxn[i]; // 选最大 flag[i] = false;return;
}
void dfs1(int i, int fa) {flag[i] = true;for (int t = 0; t < g[i].size(); t++) {int v = g[i][t].to, tot = g[i][t].tot;if (!flag[v]) {if (pos[i] == v) swap(maxn[i], n_maxn[i]); // v 在最大上 换次大 dp1[i][0] = dp2[i] - max(dp[v][0], dp[v][1] + tot); // 减去 v 做贡献 dp1[i][1] = dp1[i][0] + maxn[i];if (fa != -1) dp1[i][1] = max(dp1[i][1], dp1[i][0] + dp1[fa][0] + vg[i] - max(dp1[fa][0], dp1[fa][1] + vg[i])); // i 重做中点  dp2[v] = dp[v][0] + max(dp1[i][0], dp1[i][1] + tot);if (pos[i] == v) swap(maxn[i], n_maxn[i]); // 还原 dfs1(v, i);}}ans = max(ans, dp2[i]);return;
}
int main() {scanf("%d", &n);for (int i = 1; i < n; i++) {int x, y, z;scanf("%d %d %d", &x, &y, &z);g[x].push_back(edge({y, z}));g[y].push_back(edge({x, z}));}dfs(1); // 初始根 ans = dp2[1] = dp[1][0];dfs1(1, -1); // 换根 printf("%d\n", ans);return 0;
}

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！