逃离迷宫类问题总结(DFS深搜)
逃离迷宫是DFS深搜的例题。没错,和摄像头模型一样重要!!!
X 逃离迷宫1
问题描述
有一个方格迷宫,我们可以将它看作一个n*m的矩阵,每个方格表示一个房间,方格中有数字0和1,数字0表示该房间是空的,可以顺利通过,数字1表示该房间有怪兽,不能通过。
一开始何老板位于左上角的方格(坐标[1,1]位置),他要走到右下角的出口(坐标[n,m]位置),每一步何老板只能往下或往右走。
他想知道总共有多少条可行的线路?输入格式
第一行,两个整数n和m
接下来是一个有数字0和1构成的n*m的矩阵,表示迷宫输出格式
一个整数,表示可行路线的条数。
样例输入
4 5
0 0 0 0 1
0 0 1 0 0
1 0 1 1 0
1 0 0 0 0样例输出
3
提示
1<=n,m<=20
我们可以简单模拟一下 :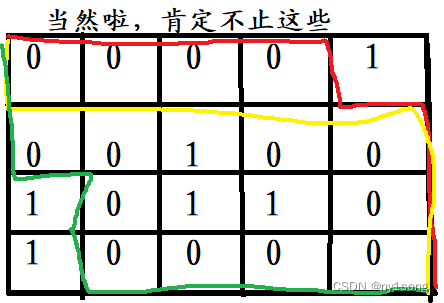
分析:
深搜类似于一个递归过程——讨论每一个位置的下一步,再讨论每个位置下一步的下一步,直到找到终点为止。
这是一个二维数组,我们要记录每一个点的位置(x,y)并按题目要求讨论(x+1,y)(x,y+1)...... 当然,不能死递归,每一次讨论都要判断其位置是否为终点。(出示一下DFS函数吧)
void dfs(int x,int y)
{if(x==n && y==m){ans++;//ans为全局变量return;}//判断终点else{if(x+1<=n&&a[x+1][y]==0) dfs(x+1,y);if(y+1<=m&&a[x][y+1]==0) dfs(x,y+1);}//依次讨论下一步
}
Y 逃离迷宫2
问题描述
有一个方格迷宫,我们可以将它看作一个n*m的矩阵,每个方格表示一个房间,方格中有数字0和1,数字0表示该房间是空的,可以顺利通过,数字1表示该房间有怪兽,不能通过。
一开始何老板位于左上角的方格(坐标[1,1]位置),他要走到右下角的出口(坐标[n,m]位置),每一步何老板可以往上、下、左、右走。
他想知道最少需要几步就可以走出迷宫?输入格式
第一行,两个整数n和m
接下来是一个有数字0和1构成的n*m的矩阵,表示迷宫输出格式
一个整数,表示最小步数。若无解,输出-1
样例输入
4 5
0 0 0 0 0
0 1 1 1 0
0 1 0 0 0
0 0 0 1 0样例输出
7
提示
1<=n,m<=20
和迷宫1有一些区别,这道题是求最少步数,迷宫1是求总路程数。 和上题意思差不多,就不模拟了。直接上思路——
分析:
这道题呢,一共有四种方向,可以用增量数组(我就没用了),而且要求步数,就添加一个step参数,方便计算。但是,只单纯的加上两个方向,就会出现在同一个地方反复跳跃的情况,不就死循环了吗? 那怎样才能避免发生这种情况呢?——每次讨论对a[x][y]进行标记(首标记为0,尾标记为1)这一步是我们制胜的关键!
a[x][y]=1;
if(x+1<=n&&a[x+1][y]==0) dfs(x+1,y,step+1);
if(y+1<=m&&a[x][y+1]==0) dfs(x,y+1,step+1);
if(x-1>=1&&a[x-1][y]==0) dfs(x-1,y,step+1);
if(y-1>=1&&a[x][y-1]==0) dfs(x,y-1,step+1);
a[x][y]=0;这样交上去答案不会有问题,但是,会TLE !!! 那就必须进行优化了。 我们先来看看下面这个简单的问题 :
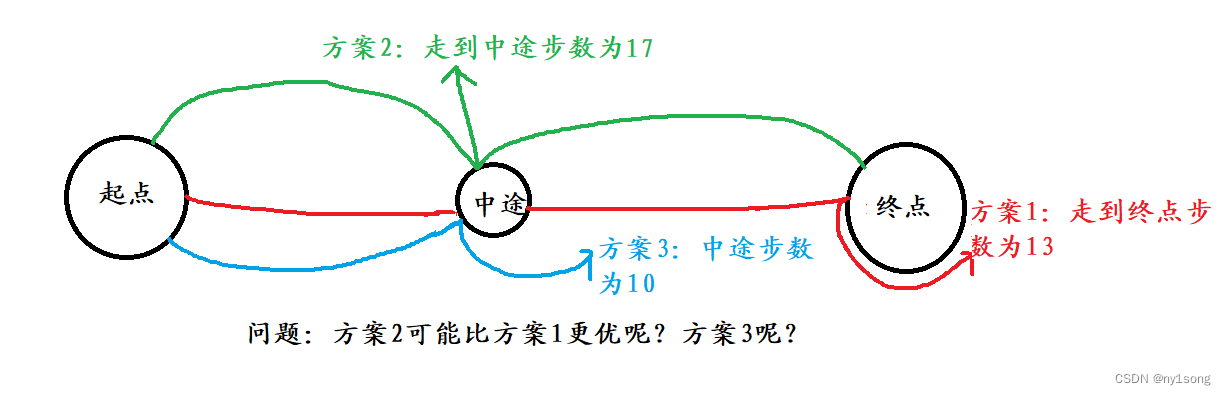
没错,方案2肯定不可能比方案1更优,而方案3还有一点可能——所以,举一反三,我们可以用b数组来记录到达每一个点的步数,及时舍弃。这个判断呢最好是放在终点判断前。
if(b[x][y]>step) b[x][y]=step;
else return;
if(x==n && y==m){ans=ans>step?step:ans;return;
}d逃离迷宫3
问题描述
有一个方格迷宫,我们可以将它看作一个n*m的矩阵,每个方格表示一个房间,每个方格中都有数字。数字-1表示该房间内有陷阱,不能通过。如果格子里是>=0的数字,表示该房间中有怪兽,数字代表该怪兽的杀伤力,何老板通过该房将会失去对应数值的生命值。
一开始何老板位于左上角的方格(坐标[1,1]位置),他要走到右下角的出口(坐标[n,m]位置),每一步何老板可以往上、下、左、右走。 他想知道最少需要失去多少生命值就可以走出迷宫?输入格式
第一行,两个整数n和m
接下来是一个由整数构成的n*m的矩阵,表示迷宫输出格式
一个整数,表示最小失去的生命值。若无解,输出-1
样例输入
4 6
20 100 50 -1 -1 10
10 -1 50 10 10 5
10 -1 70 -1 10 -1
20 30 20 50 20 10样例输出
190
提示
1<=n,m<=30
-1<=矩阵中的数字<=500
迷宫3 和迷宫2差不多,算是升级款。但数据更大,就得继续优化。那问题来了——如何优化呢? 1.记忆化数组(和上题一样)
2.可行性减枝:如果还未走到终点,消耗的生命值就大于之前记录的答案,肯定不会是最优。
3.最优化减枝:用minn变量(输入时记录)所有怪兽的最小杀伤力,如果走到非终点的一点,步数未超过minn,那也就不行呗。
//1.记忆化数组
if(step=ans) return;
//3.最优化减枝
if(step+(n+m-x-y)*minn>=ans) return; 总结一下——
DFS就相当于递归,但是多数题纯递归都会超时,所以这类问题重在优化。以上👆便是我们已学的几种优化方式——非常重要!!!
完美结束(全场欢呼👏~
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!