ArabellaCPC 2019（夏季个人赛第三场）

D - Meeting Bahosain

题意：给一个a数组，加减一个b数组的任意值，看能不能使得a数组全部相等。
思路：如果存在某种转化，使得a的全部元素可以转化为 a i a_i ai​，那么对于a中任意元素都可以两两进行转化。就比如： ∣ a i − a i − 1 ∣ = ∣ a i + 1 − a i ∣ = x |a_i-a_{i-1}|=|a_{i+1}-a_{i}|=x ∣ai​−ai−1​∣=∣ai+1​−ai​∣=x，且差值x在b数组中得以出现，那么我们可以认为$a[i],a[i-1],a[i+1]$之间两两都可以直接或间接转换，可以印证之前的推理。所以如果我们所有的间距 $△x$ ,每一个数都可以由 $b$ 数组间接或直接凑出，那么我们可以说这个数组a的每一个元素之间可以两两转化，那必然可以相等。
由算数基本定理可知： 若 △ x = k 1 ⋅ b 1 + k 2 ⋅ b 2 + k 3 ⋅ b 3 + k 4 ⋅ b 4 … … △x=k_1·b_1 + k_2·b_2 +k_3·b_3 + k_4·b_4 …… △x=k1​⋅b1​+k2​⋅b2​+k3​⋅b3​+k4​⋅b4​……，那么这一组间距可以被b间接或直接得到，我们提取这一坨式子的公因式，很明显是$gcd(b数组)$，所以如果$△x$整除 $gcd(b)$ ，那么就存在一个系数 $k$ 使得，$△x=k\ast gcd(b)$，所以我们说这一组间距可以被凑出。同理，如果要使得每一组间距被凑出，那么就相当于求出整个$数组（△x）$的gcd，让这个值整体被 $gcd(b数组)$ 整除，那么每一组间距就都可以被凑出，那么每一个a都可以直接或间接转化。

#include
using namespace std;
const int N=1e6+100;
int n, m;
int a[N], b[N];
int gcd1, gcd2;
int main()
{ios::sync_with_stdio(false);//不用这个真的过不了吗？？？cin.tie(0);cin >> n >> m;for(int i = 0; i < n ; i++){cin >> a[i];if(!i) gcd1 = a[i];else {gcd1 = __gcd(gcd1, abs(a[i] - a[i-1]));}}for(int i = 0; i < m ; i++){cin >> b[i];if(!i) gcd2 = b[i];else gcd2=__gcd(gcd2, b[i]);}if(gcd1%gcd2 && n != 1)cout << "No";else cout << "Yes"; //特判n=1相当于数组全部相等return 0;
}

J - Thanos Power

题意：给一个数n，每次我们可以加或者减去 1 0 k 10^k 10k 大小的数，求凑出这个n 。
思路：首先可以发现当前状态总是跟前一个状态有关，贪心总无法得到最优解，只能考虑dp。
对于dp的状态表示比较容易想， dp i , 0 \text{dp}_{i,0} dpi,0​表示的是前i个数，第i位是通过下降得到的步数最小值，此处下降就是指从高位减下来，比如100到80。同理， dp i , 1 \text{dp}_{i,1} dpi,1​表示的是前i个数，第i位是通过上升得到的步数最小值。
状态转移：如果这一维是从0上升得到的数字，那么前一维不论上升还是下降都与这一维无关，所以$dp[i][1]=\min (dp[i-1][0],dp[i-1][1])+x即可;$如果这一维是从高位下降得来的数，那么如果前一维也是下降的话，可以让前一维少下降一位，很明显这样做可以使得当前为得到这个数的步数更小。同理，如果前一维是从低位升上来的，这一维需要从高位降，那没有办法，只能让前一维多走一步，再加上当前位数从高位降下来的值。$dp[i][0]=\min (dp[i-1][0]-1,dp[i-1][1]+1)+10-x$。

#include 
#include 
#include 
using namespace std;
typedef long long LL;
int x;
const int N = 1e5+10;
int dp[N][2];
int main()
{string st;cin>>st;int n=st.size();x=st[0]-'0';dp[0][1]=x;//上升dp[0][0]=11-x;//下降for(int i=1;i<n;i++){x=st[i]-'0';dp[i][0]=min(dp[i-1][0]-1,dp[i-1][1]+1)+10-x;//前一个数降少降1，前一个数升多升1dp[i][1]=min(dp[i-1][0],dp[i-1][1])+x;}cout<<min(dp[n-1][0],dp[n-1][1])<<endl;
}

G - Card Game

题意：A，B玩家，每个人有n张牌，分别是1~n的面值。打n个回合，打完一张牌就弃到牌库，手牌会在n个回合后打完，只有A玩家当前牌的面值大于B玩家当前打出的牌的面值才会得分（得分大小为当前牌的面值），如果两个人随机出牌，求A玩家得分的期望。

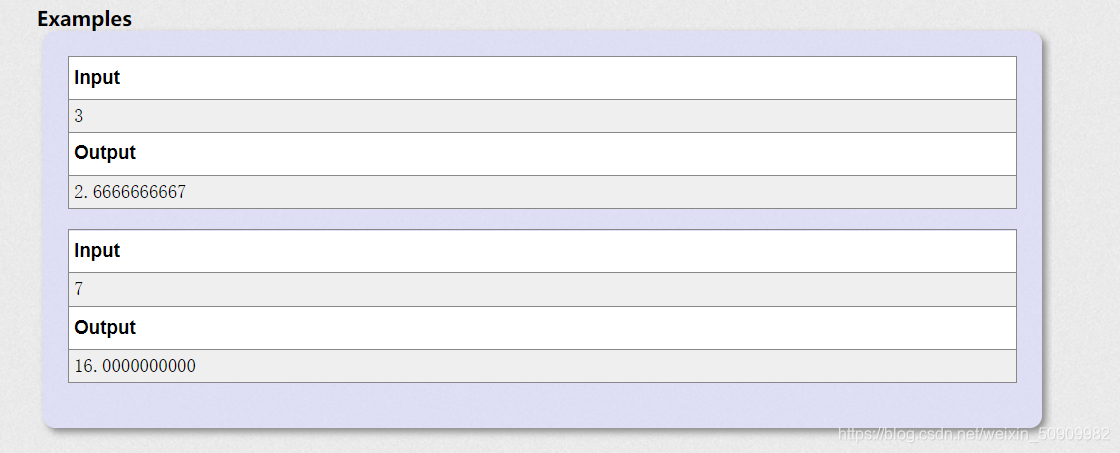
思路：两人相对出牌，一共n轮，对k这张牌来说，只有k-1张牌对答案有贡献，可以从贡献的角度理解并得出公式： ∑ i = 1 n i ∗ ( i − 1 ) n \sum_{i=1}^n\dfrac {i*(i-1)} {n} i=1∑n​ni∗(i−1)​
这个公式同样也具有直观上的含义，比如 $\text{A}$ 玩家打出一张牌 $k$ ，此牌出现在第 $i$ 个位置的概率是 1 n \dfrac {1} {n} n1​ ,那么对于此位置的排序，具有 A n − 1 n − 1 A_{n-1}^{n-1} An−1n−1​种可能性，对于任意一种可能性，我们考虑对手第 $i$ 个位置的牌如何能使得A玩家得分，所以得分的顺序为 ( i − 1 ) ∗ A n − 1 n − 1 (i-1)*A_{n-1}^{n-1} (i−1)∗An−1n−1​,所以对两个人的牌序来说，不得分的位置是一直在变化的，但是得分的位置也总是相对静止的——因为 A n − 1 n − 1 ∗ ( i − 1 ) A n − 1 n − 1 = ( i − 1 ) \dfrac {A_{n-1}^{n-1}*(i-1)} {A_{n-1}^{n-1}}=(i-1) An−1n−1​An−1n−1​∗(i−1)​=(i−1)，所以实际得分为 ∑ i = 1 n i ∗ ( i − 1 ) n \sum_{i=1}^n\frac { i*(i-1)} {n} i=1∑n​ni∗(i−1)​ 。

#include 
#include 
#include 
using namespace std;
typedef long long LL;const int N = 1e5+10;
int dp[N][2];
int main()
{double n;cin>>n;double res=0;double y=n;for(int i=2;i<=n;i++){y=(i-1)/n;res=res+i*y;}printf("%.10lf\n",res);
}

H - Steaks

题意：煎 $n$ 个牛排，每个牛排有正反面，每一面耗时五分钟，你有k个锅，每个锅最多放入两个牛排，煎熟的最短时间。
思路：此题比较离谱的就是这个样例：

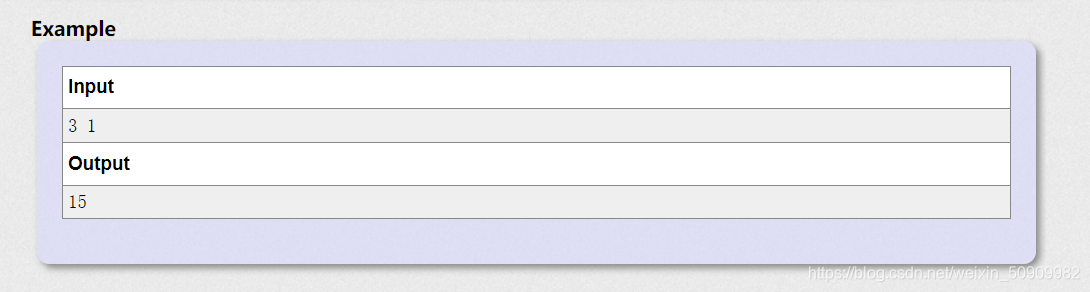
它是由正正，反正，反反实现了一个锅15分钟煎熟牛排，这中间你可以把一个牛排单拎出来，放在一边，反正我们只需要把时间效率拉满，至于这个过程的可行性只有出题人才知道。
虽然一个牛排可以花哨的煎，但对于一个牛排起码不可以同时煎正反面。所以如果$n\le 2\ast k$，那么锅可以一次性放下所有牛排，牛排不能分身，必须等10分钟才能煎完。
若 $n>2\ast k$，且假设n可以整除掉k，比如四个个牛排一个锅，显然 正正 反反 正正 反反 效率最高，总共花了20分钟（ n k ∗ 5 \dfrac{n}{k}*5 kn​∗5）。如果n不可以整除掉k，我们也可以通过x轮，间接的用偶数拉满效率，一直到剩下最后的三个牛排，我们可以沿用最开始样例的方法，这样就可以用1一个锅把这三个牛排的效率也拉满。

#include 
#include 
#include 
using namespace std;
typedef long long LL;int main()
{LL n,k,res=0;cin>>n>>k;LL x;int y=2*k;if(y>=n){cout<<10<<endl;}else{if(n%k==0){  cout<<n/k*5<<endl;}else{cout<<n/k*5+5<<endl;}}
}

C - Check The Text

题意：模拟打字鸡！！！

#include 
using namespace std;
int n, m, daxie;
string str, res, op;
signed main() 
{cin >> n;getchar();getline(cin, str);cin >> m;while (m --) {cin >> op;if (op == "CapsLock") {daxie^=1;} else if (op == "Backspace") {if (!res.empty()) res.pop_back();} else if (op == "Space")  res += " ";else {if (daxie) {   char x = op[0];res += x - 32;} else res += op;}}if (res == str)  cout << "Correct" << endl;else cout << "Incorrect" << endl;
}

A - Is It Easy ?

题意：搞蛇皮

#include 
#include 
#include 
using namespace std;
int main()
{int n,m;cin>>n>>m;cout<<n*m<<endl;
}

M - Two Operations

题意：给字符串 $s$ ，你可以进行给定的两个操作，使得串的字典序最大。

1. 交换字符串任意两个字符位置
2. 将相邻的相同字母合成为一个字典序+1的一个字符，如bb——c。

思路：字典序是贪心策略求得的，则存在高位能大就大的原则。根据操作1可以使得操作2的相邻不复存在了，所以只要存在相同字母就把他们合成并存下来，最后我们循环字母表，ascii码值大的先输出。复杂度大概是$\text{O}(n)$。

#include 
#include 
#include 
using namespace std;
typedef long long LL;
const int N = 1e5+10;
char str[N];
int a[30];
int main()
{string st;cin>>st;int n=st.size();for(int i=0;i<n;i++){a[st[i]-'a']++;}for(int i=0;i<=24;i++){if(a[i]>=2){if(a[i]%2==0){a[i+1]=a[i+1]+a[i]/2;a[i]=0;}else{a[i+1]=a[i+1]+a[i]/2;a[i]=1;}}}int ct=0;for(int i=25;i>=0;i--){while(a[i]){a[i]--;str[ct++]=i+'a';}}for(int i=0;i<ct;i++){cout<<str[i];}puts("");
}

B - Road to Arabella

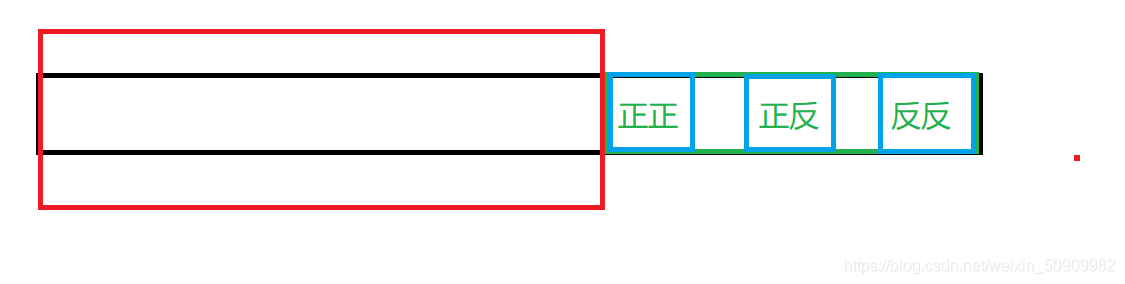
题意：Ayoub and Kilani 玩游戏， Kilani先开始。给定$n$和$k(k<=n)$，每次可以给n减去一个数x,这个x是玩家自己选但是x的范围必须在$(1\le x\le \max (1,n-k))$，如果一个玩家的 $n=0$ ，即无法操作的时候判负。
思路：从这个x的范围可以判断如果$n=k||n=k+1$时，只能选择给$n减1$,非常被动。因为这个游戏谁的$n=0$谁就输了，所以当$n>k+1$时，肯定存在一个中间状态$m=k||m=k+1$，然后两个人都只能拿1并持续到游戏结束。 所以对于先手的Kilani来说，他可以直接把m拿到一个偶数的状态，且$m=k||m=k+1$,这样对手不得不一步一步的看着$n=0$的到来。
所以$n>k+1$先手必胜。而$n=k||n=k+1$时已经分析过了，谁是偶数谁就只能一步步看着自己输掉比赛。

#include 
#include 
#include 
using namespace std;
typedef long long LL;int main()
{int t;cin>>t;while(t--){int n,m;cin>>n>>m;if(n-m<=1) {if(n%2==0){cout<<"Ayoub"<<endl;}else cout<<"Kilani"<<endl;}else cout<<"Kilani"<<endl;}}

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！