week10
A-签到题
题目:
东东有一个字符串X,该串包含偶数个字符,一半是 S 字符,一半是 T 字符。东东可以对该字符串执行 1010000 次操作:如果存在 ST 是该串的子串,则删除掉最左边的 ST。
即 TSTTSS⇒TTSS、SSSTTT⇒SSTT⇒ST⇒空。
Input:
(2 ≦ |X| ≦ 200,000)
Output:
输出最终串的长度。
Sample Input:
TSTTSS
Sample Output:
4
题目分析:
该题的实现并不难,只需要按照题意对输入的字符串,一直进行ST子串的判断即可。
问题在于如果只是利用sring的erase操作,每次对进行了删除操作后的子串都要进行再次判断是否还存在符合题意的子串的话,就会出现两重循环,会导致超时!!!不可取。
所以改用栈的形式,动态的进行判断删除,当栈顶元素为S且下一个要放入栈顶的元素为T的时候,说明找到了符合条件的子串,删除;否则将元素压入栈内。
代码:
#include
#include
#include
#include
using namespace std;
int main()
{string s;cin>>s;stack q;for(int i=0;i B-东东转魔方
题目:
东东有一个二阶魔方,即2×2×2的一个立方体组。立方体由八个角组成。
魔方的每一块都用三维坐标(h, k, l)标记,其中h, k, l∈{0,1}。六个面的每一个都有四个小面,每个小面都有一个正整数。
对于每一步,东东可以选择一个特定的面,并把此面顺时针或逆时针转90度。
请你判断,是否东东可以在一个步骤还原这个魔方(每个面没有异色)。
Input:
输入的第一行包含一个整数N(N≤30),这是测试用例的数量。
- 对于每个测试用例, 第 1~4个数描述魔方的顶面,这是常见的2×2面,由(0,0,1),(0,1,1),(1,0,1),(1,1,1)标记。四个整数对应于上述部分。
- 第 5~8 个数描述前面,即(1,0,1),(1,1,1),(1,0,0),(1,1,0)的公共面。四个整数 与上述各部分相对应。
- 第 9~12 个数描述底面,即(1,0,0),(1,1,0),(0,0,0),(0,1,0)的公共面。四个整数与上述各部分相对应。
- 第 13~16个数描述背面,即(0,0,0),(0,1,0),(0,0,1),(0,1),(0,1,1)的公共面。四个整数与上述各部分相对应。
- 第 17~20 个数描述左面,即(0,0,0),(0,0,1),(1,0,0),(1,0,1)的公共面。给出四个整数与上述各部分相对应。
- 第 21~24 个数描述了右面,即(0,1,1),(0,1,0),(1,1,1),(1,1,0)的公共面。给出四个整数与上述各部分相对应。
换句话说,每个测试用例包含24个整数a、b、c到x。你可以展开表面以获得平面图:
如下所示。
+ - + - + - + - + - + - +
| q | r | a | b | u | v |
+ - + - + - + - + - + - +
| s | t | c | d | w | x |
+ - + - + - + - + - + - +
| e | f |
+ - + - +
| g | h |
+ - + - +
| i | j |
+ - + - +
| k | l |
+ - + - +
| m | n |
+ - + - +
| o | p |
+ - + - +
Output:
对于每个测试用例,魔方如果可以至多 "只转一步" 恢复,输出YES,则输出NO。
友情提示:如果能思考一下解题框架的设计是最好的,一上来就莽很痛苦!
友情提示:如果能思考一下解题框架的设计是最好的,一上来就莽很痛苦!
友情提示:如果能思考一下解题框架的设计是最好的,一上来就莽很痛苦!
Sample Input:
4
1 1 1 1 2 2 2 2 3 3 3 3 4 4 4 4 5 5 5 5 6 6 6 6
6 6 6 6 1 1 1 1 2 2 2 2 3 3 3 3 5 5 5 5 4 4 4 4
1 4 1 4 2 1 2 1 3 2 3 2 4 3 4 3 5 5 5 5 6 6 6 6
1 3 1 3 2 4 2 4 3 1 3 1 4 2 4 2 5 5 5 5 6 6 6 6
Sample Output:
YES
YES
YES
NO
题目分析:
该题关键在于理解魔方的转动方式以及仔细理清各个小面的下标关系。
首先对于魔方而言,要最多一次转动还原成六个面没有异面的情况,分为两种情况:
- 不转动:这种要求魔方初始六个面就是各个面同色的情况。
- 转动一次:因为对于魔方而言,每一次转动90度,都会影响到四个面(两个对面),所以零外两个面(另外一个对面)必须是已经同色的。
- 左右面同色
- 上下面同色
- 前后面同色
- 每组形式,都要求另外四个面可以通过顺时针或者逆时针转动90度完成同色,这就可以通过将另外四个面展开,首先每个面的旋转方向的两个小面的值必须相同,然后判断相邻两个面的斜对角的两对相同。(注意四个面形成的是一个环哦,即使展开了也不要忘记,容易出错)(说起来有点不好理解,看图吧)(另外,各个面的展开图的下标很容易搞错,最好可以自己折一个纸魔方,便于画展开图)
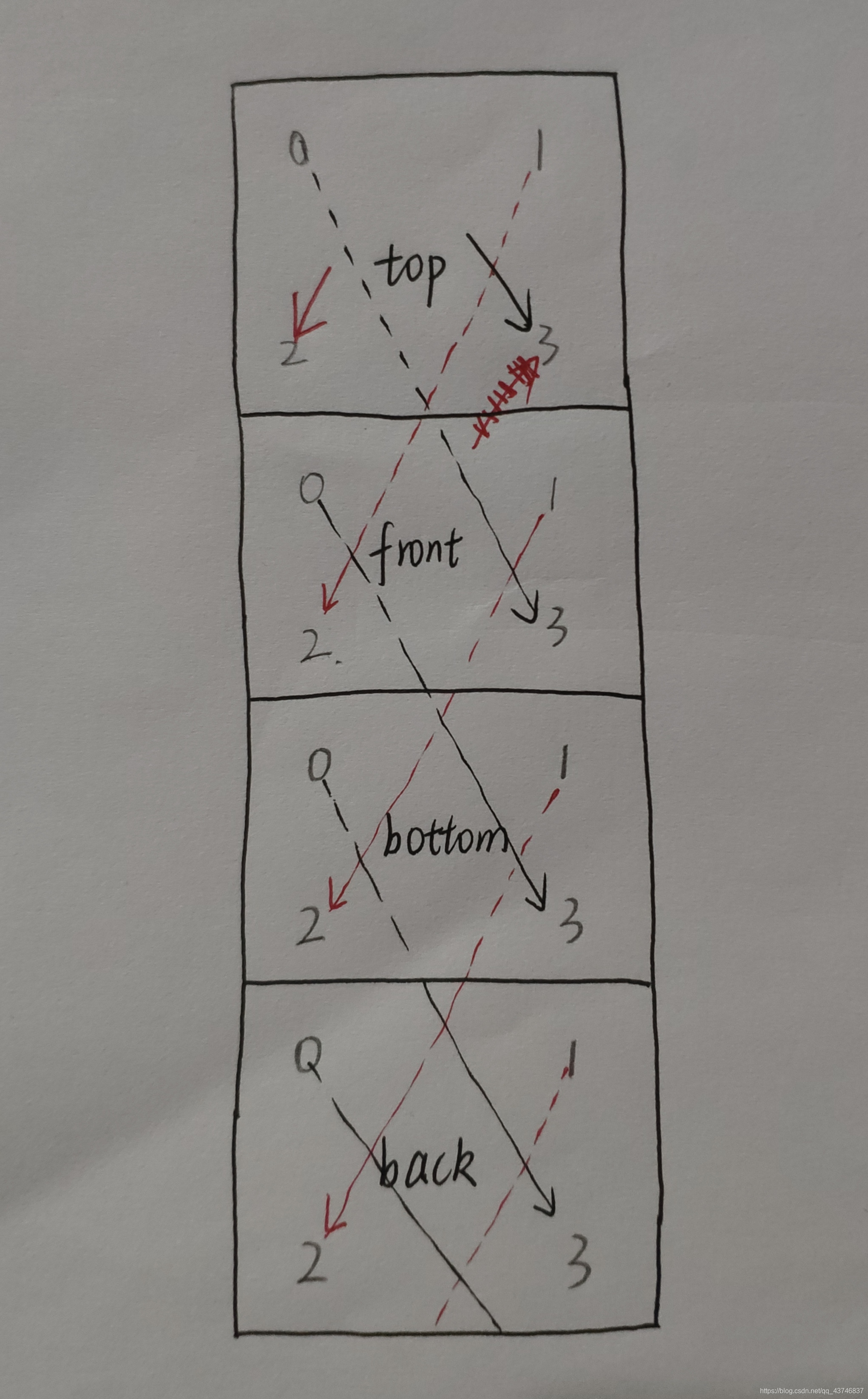
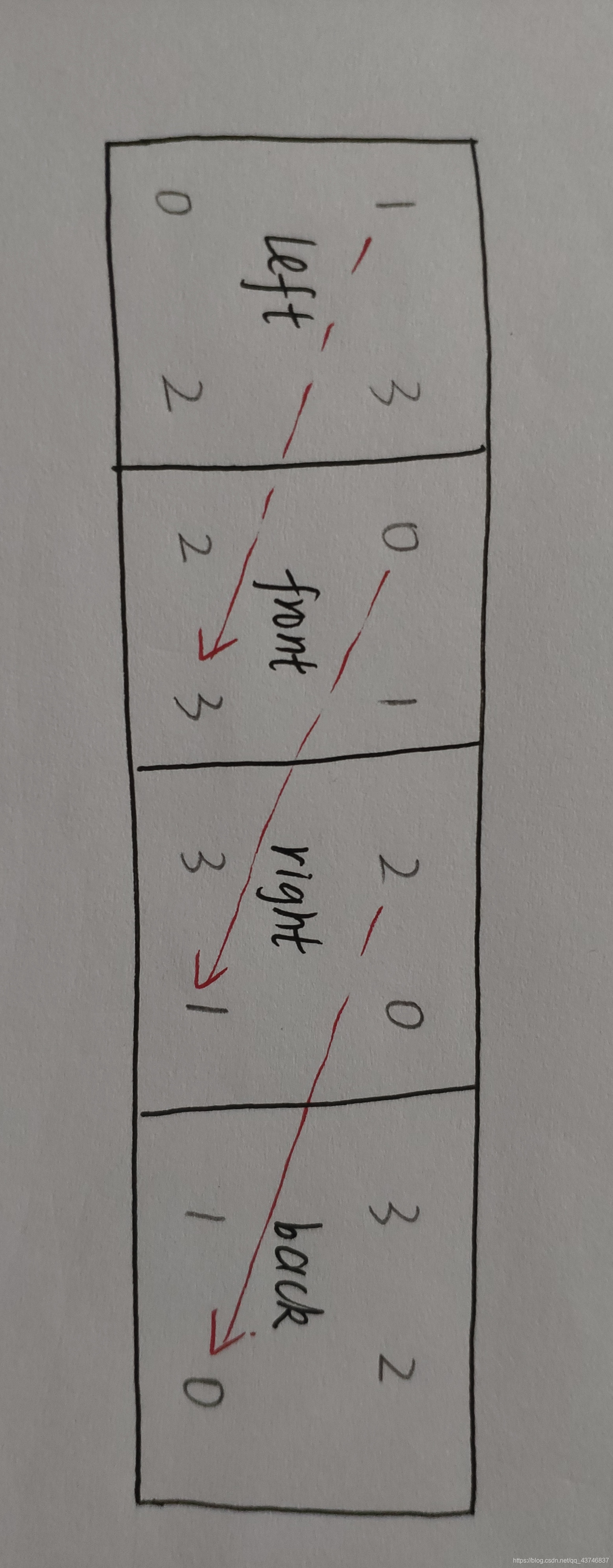
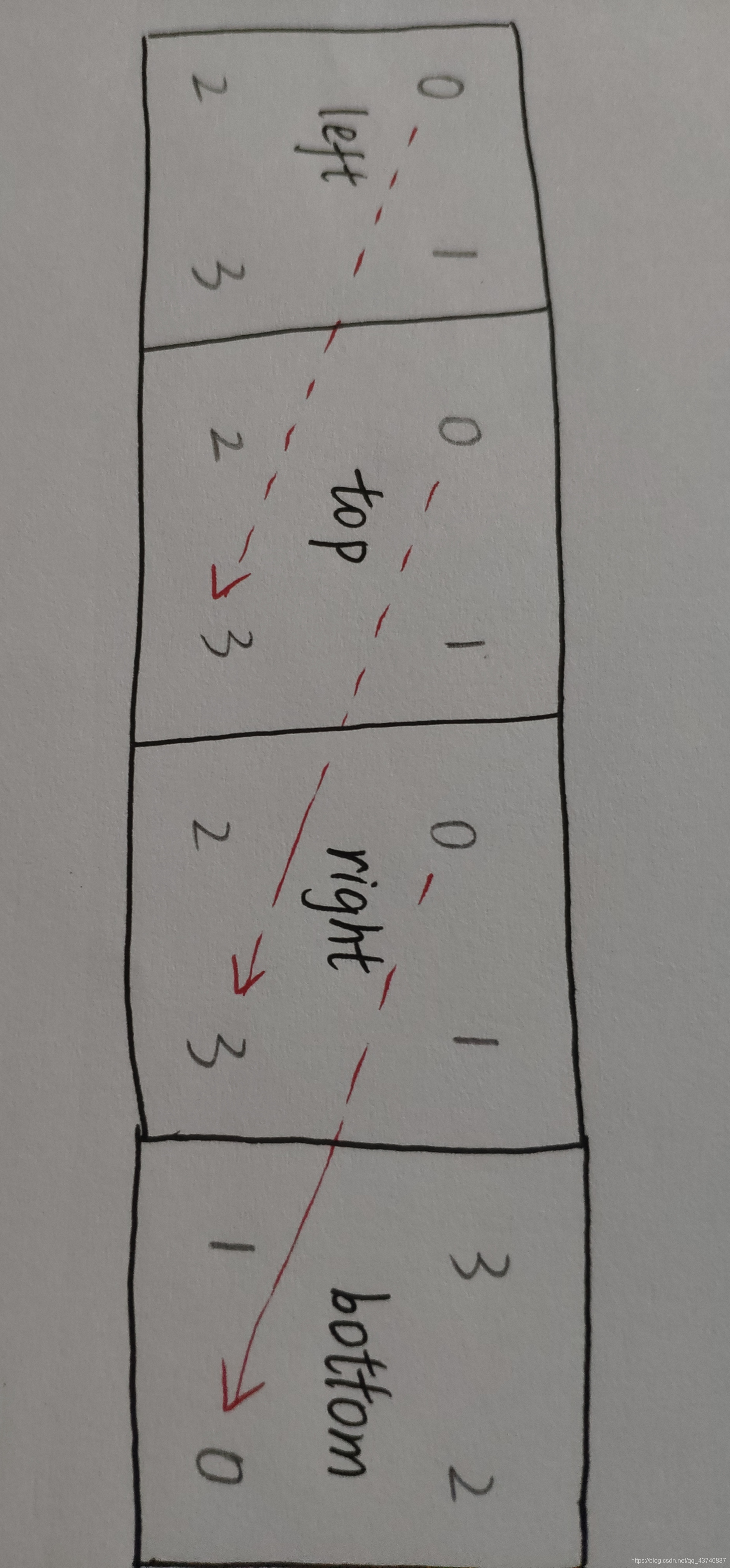
代码:
#include
#include
using namespace std;
int top[4],bottom[4],rright[4],lleft[4],front[4],back[4];bool tongmian(int p[])
{for(int i=1;i<4;i++){if(p[i-1]!=p[i]){return false;}}return true;
}
bool duijiao(int p[])
{if(p[0]==p[2]&&p[1]==p[3]){return true;}return false;
}
bool duijiao1(int p[])
{if(p[0]==p[1]&&p[2]==p[3]){return true;}return false;
}
bool trans1()//左右面同色
{if(tongmian(lleft) && tongmian(rright)){if(duijiao(top) && duijiao(front) && duijiao(bottom) && duijiao(back)){if(top[0]==front[3] && front[0]==bottom[3] && bottom[0]==back[3] && back[0]==top[3]){//cout<<"左右1"<>N;while(N--){for(int i=0;i<4;i++)//顶面 {cin>>top[i];}for(int i=0;i<4;i++)//前面 {cin>>front[i];}for(int i=0;i<4;i++)//底面 {cin>>bottom[i];}for(int i=0;i<4;i++)//背面 {cin>>back[i]; }for(int i=0;i<4;i++)//左面 {cin>>lleft[i];}for(int i=0;i<4;i++)//右面 {cin>>rright[i];}if(tongmian(top)&&tongmian(bottom)&&tongmian(front)&&tongmian(back)&&tongmian(rright)&&tongmian(lleft)){cout<<"YES"<
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!