白话支持向量机（SVM）原理之--二狗挑土豆

引例：挑土豆大作战

二狗黑心厨房开业啦，你被抽中作为幸运观众可以去厨房参观，发现案板上有两类土豆，如果充了二狗888vip会员，给你做饭就用好土豆，如果没充会员，给你做饭就用坏土豆。这时二狗递给你一把刀，说如果你不用手触摸土豆的情况下用一把刀就能将好土豆和坏土豆分开，且不能把土豆分错，就送你一年888vip会员，这时你应该怎么办？

如何把挑土豆抽象化一点？–感知机模型

假设二狗稍微有点缺心眼，把好土豆和坏土豆已经聚好类了，如下图所示：

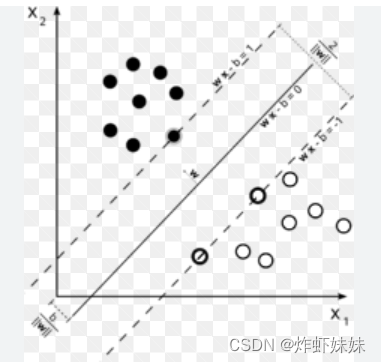
可以把实心圆点想象成好土豆，空心圆点想象成坏土豆，只要在两类土豆的中间给它来一刀，自然就能把好坏土豆分开。

但是，可以很明显的发现，有无数种下刀方式，为了拿到888vip，肯定要选择最稳妥的下刀方式，那么怎么下刀方式才是最好的呢？

答：你可以在脑内迅速的计算一下，对每一种下刀方式把每一个土豆分错的概率进行加和，最后选择一个总分错概率最小的下刀方式。

• 好土豆：正例；坏土豆：负例；刀：超平面
• 感知机能有效的前提的正例与负例是线性可分的。
• 感知机选择超平面的方式：损失函数最小。损失函数通常选为误分类点到超平面的总距离。

下刀的时候每个土豆都很重要吗？–硬间隔支持向量机

到这里，聪明的观众已经发现了，对各种下刀方式计算一下总误差是工作量很大且很蠢笨的，那我们能不能研究一下，怎么衡量好的下刀方式更简单呢？

如下图所示，从直观上来说，最深色的那一刀最好，因为它离正例和负例都比较远，这样你在训练案板上练好了，万一测试案板上土豆变多了一些，或者你手突然抖了一下，也比其他下刀方式分错的概率小。

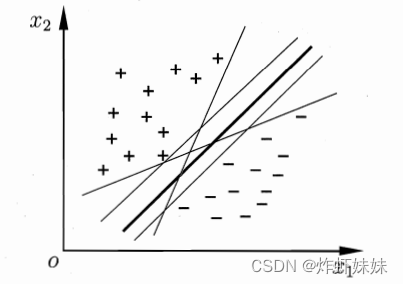
在SVM中，我们称深色的这一个超平面“鲁棒性”最好，即对非训练集的样本泛化能力最强。鲁棒是Robust的音译，也就是健壮和强壮的意思。所谓“鲁棒性”，也是指控制系统在一定（结构，大小）的参数摄动下，维持其它某些性能的特性。

到这里，更聪明的观众已经想到了，在下刀的时候，只有离刀最近的土豆是重要的，是最有可能被分错的，我们在下刀的时候只要关注这些土豆就行。但是，如何挑出这些需要被关注到的土豆呢？

挑出需要关注的土豆–在SVM中找到支持向量
给自己的手抖一些机会–找寻最优超平面转化为找寻最大间隔

引例升级：没办法一刀将土豆分开怎么办？

round1：现在有好土豆和坏土豆在案板上排成一排，给你一把刀，如何在只切一刀的情况下使刀的一边都是好土豆，另一边都是坏土豆？

答：稍稍倾斜案板，发现好土豆都圆乎乎的，一倾斜都滚的比较远，坏土豆到处都烂了，摩擦力很大，滚的都比较近，这样好坏土豆自然就分开了。

一维无法分割的，升维到二维就可以分割了

round2：假如天不遂人意，案板倾斜后土豆都滚的乱七八糟，好土豆和坏土豆根本没有分开，你手里还是只有一把刀，如何在只切一刀的情况下把好土豆和坏土豆分开？

答：举起案板大力向上挥，发现好土豆都比较沉，向上飞了一下之后很快就下落了，坏土豆都比较轻，向上飞的很高，这样只需要在空中挥一刀就可将好坏土豆分开。

二维无法分割的，可以上升到三维进行分割

• 定理：如果原始空间是有限维，即属性数有限，那么一定存在一个高维特征空间使样本可分。

土豆怎么扔比较好？–核函数与非线性支持向量机

大家可能也从上面两个例子中发现了，如何将土豆扔起来变成了土豆好不好一刀分开的关键性因素。

• 如何将土豆扔起来–升维的方式–低维数据映射到高维

Q：不用核函数直接升维不行吗？
求解升维的线性规划需要计算样本xi与xj的内积，由于特征空间维数可能很高，甚至为无穷维，求解就变得非常困难。

• 核函数的思想：直接对特征向量的内积进行变换等价于先对特征向量做核映射然后做内积。所以其实是将需要在高维做的内积直接在低维进行处理了。
  【通俗点来说就是变为先做内积，再映射】

关于核函数的参考文献：https://www.cnblogs.com/wj-1314/p/12931799.html

• 为啥非要做内积捏？

内积（点乘）的几何意义包括：

• 表征或计算两个向量之间的夹角
• b向量在a向量方向上的投影

所以，内积是一种在某维空间里面度量其数据相似度一种手段，就是在该空间内两个向量的关系。比如两个数据点之间的距离和角度。

分类需要内积是因为内积的正负代表了数据点是位于分类边界的正方向还是负方向，从而实现分类。在高维空间，我们可以用向量内积来做线性分类。

• 什么样的函数可以作为核函数使用：
  对于一个半正定核矩阵，总能找到一个与之对应的映射。即任何半正定对称函数都可以作为核函数。

我们希望样本在特征空间中线性可分，因此特征空间的好坏对支持向量机的性能至关重要，但是在不知道特征映射的情况下，我们是不知道什么样的核函数是适合的，而核函数也只是隐式的定义了特征空间，所以，核函数的选择对于一个支持向量机而言就显得至关重要，若选择了一个不合适的核函数，则数据将映射到不合适的样本空间，从而支持向量机的性能将大大折扣。

• 核函数的基本选择经验tips：文本数据通常采用线性核；情况不明时可先尝试高斯核。

大发慈悲的老板，允许你分错几个土豆–软间隔向量机

假如经历了几次扔土豆，你发现有一个好土豆和一个坏土豆就是挨的特别近，而你其实是个隐藏的武林高手，一身轻功傍身，还会乾坤大挪移。为了使自己能拿到这个888vip，你一生气分别把这几个土豆挪移到宇宙中不同的星球上去，然后站在茫茫星河中凌空一刀，果然没有一个土豆分错。但这种过分升维的分法真的有意义吗？

背景：在现实中很难确定合适的核函数使训练样本在特征空间中线性可分，退一步说，即便恰好找到了某个核函数使训练集在特征空间中线性可分，也很难断定这个貌似线性可分的结果是不是由于过拟合所造成的。

二狗一看你是个高人，吓得连连说是他有眼不识泰山，并且谄媚的说，就算大人你分错几个土豆也可以赠你一年888vip，这时候你应该如何下刀呢？

缓解上述背景问题的办法是允许SVM在一些样本上出错，为此要引入软间隔的概念

• 软间隔支持向量机的核心思想：允许某些样本不满足约束，但是需要在最大化间隔的同时，不满足约束的样本尽可能少。利用01损失函数，使一些样本可以不满足约束

但是，这里的损失函数非凸非连续，不易求解，故人们经常用其他一些函数来替代这里的损失函数，成为“替代函数”

【注：这里的损失函数并非误差函数！损失函数更像是我允许你错，但你每错一个我都要记在小本本上。误差函数是你中规中矩的做完，但最后还是和预期结果有所偏离。】

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！