线代基础课程
一.
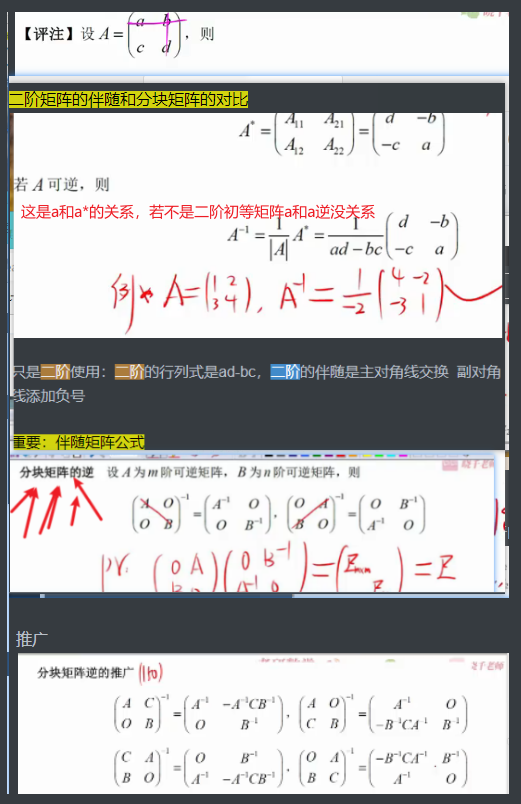
二阶矩阵A*和A有关系的,如果是分块矩阵(上三角、下三角、主队角三种的)A和A逆也有关系
这只是二阶矩阵的逆,并不是分块矩阵的逆,但是分块矩阵我们往往是分成2阶,所以容易混乱
分块矩阵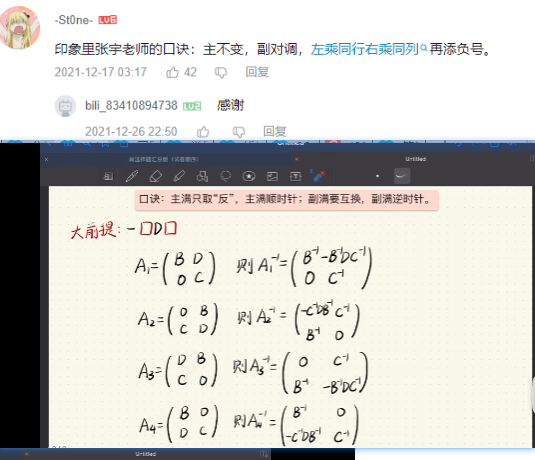
zsd:方阵的话不要只想着秩,满秩和不满秩序有6个充要条件(行列式、可逆、相关无关、齐次有解无解、非齐次有解无解、特征值是否含有0)
能相似对角化的矩阵的重要结论是秩等于非0特征值的个数
一.行列式
行列式的概念
考点:行列式的是否为0运用–必须是方阵的前提下(判断向量组线性相关和无关,判断齐次方程组有解的情况)
定义: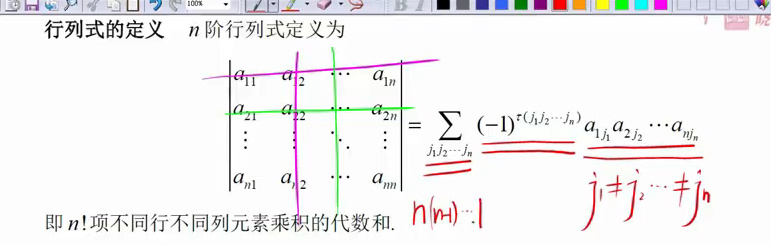
行列式的性质 5条、公式7个


e 

重要行列式
重要行列式

化成重要行列式的时候,行变换和列变化都可以
1.2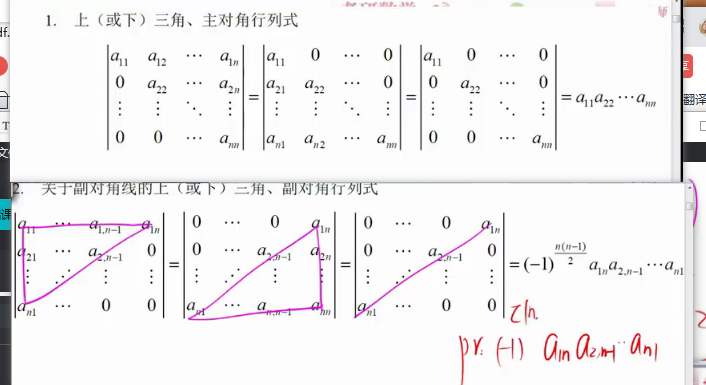
3.爪形: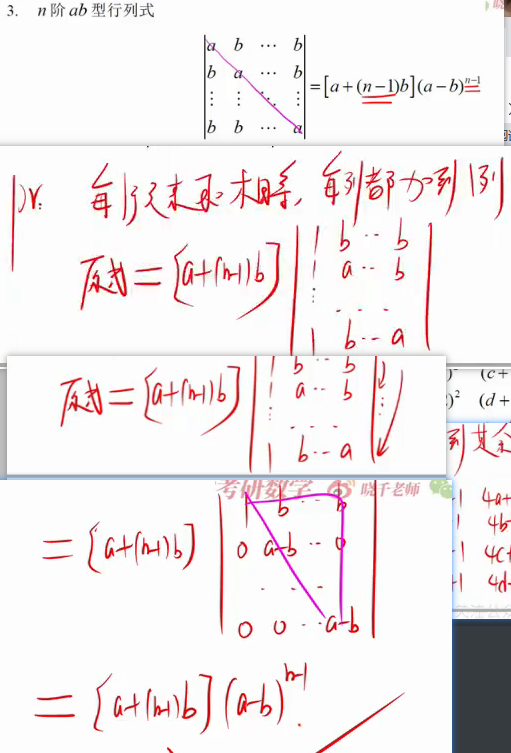
4.拉普拉斯行列式:也叫分块矩阵行列式
负对角线才需要-1的好多次方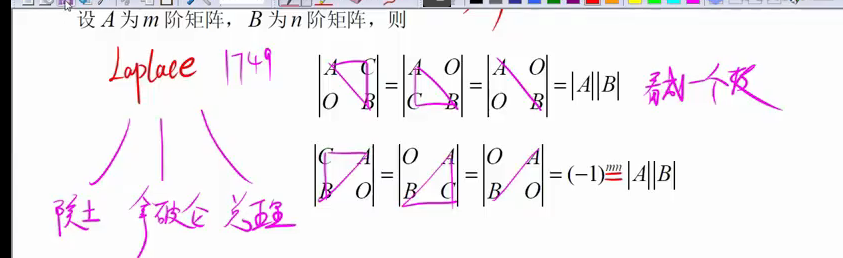
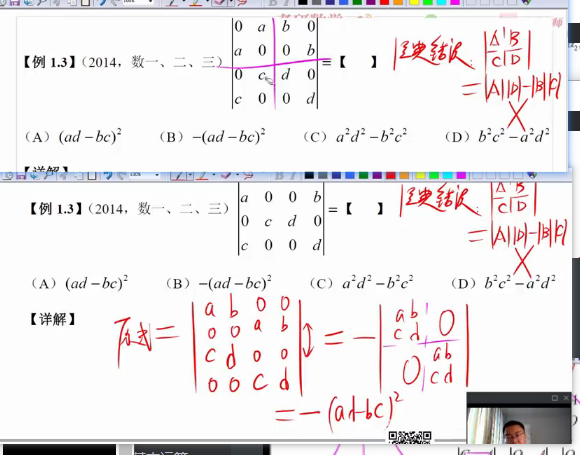
=
推广:
5.范德蒙行列式
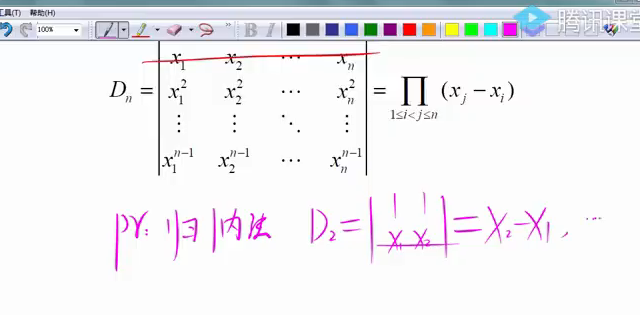
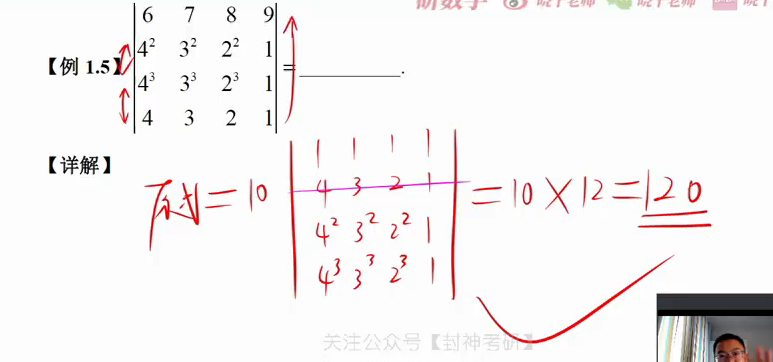
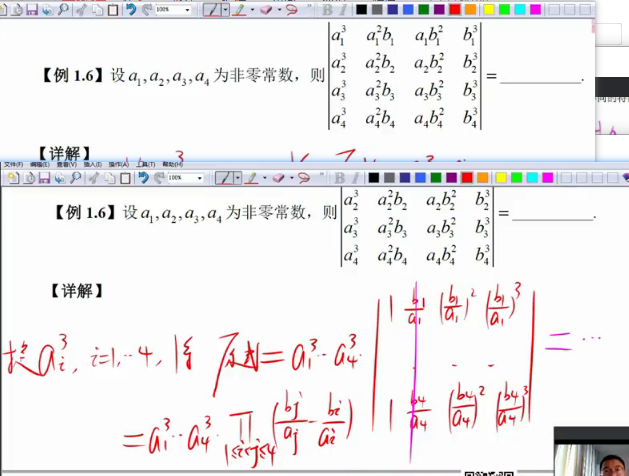
行列式展开定理
代数余子式的数值和当前行和列无关,只是符号相关
行列式是当前元素乘以代数余子式


例题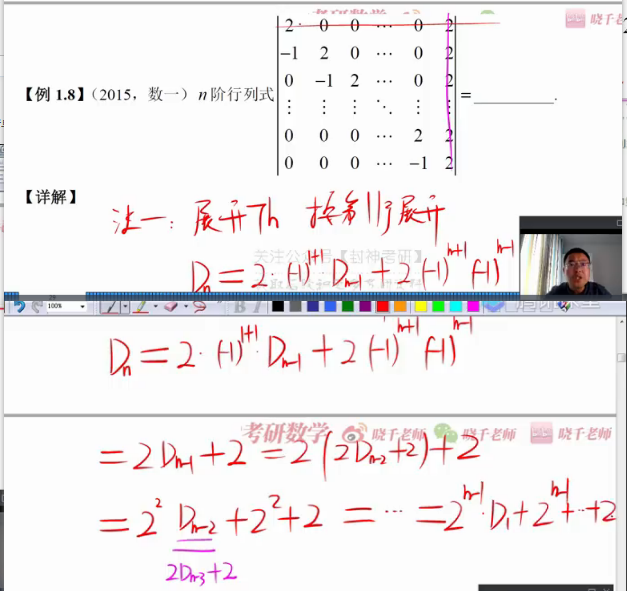
法2 化成重要行列式
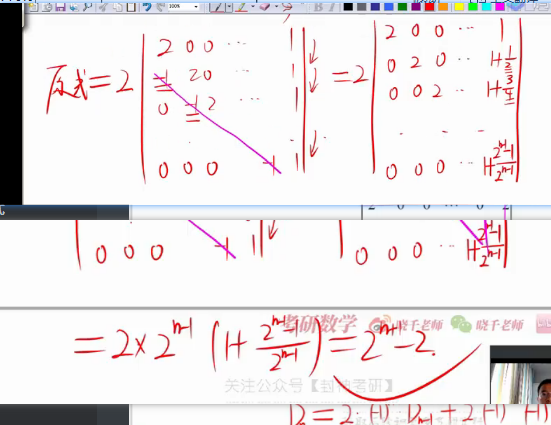
lt 
行列式的公式(7个公式 5个性质):

lt

lt
5.克莱默法则(用行列式解方程组)
要求系数矩阵是方阵,并且行列式不为0
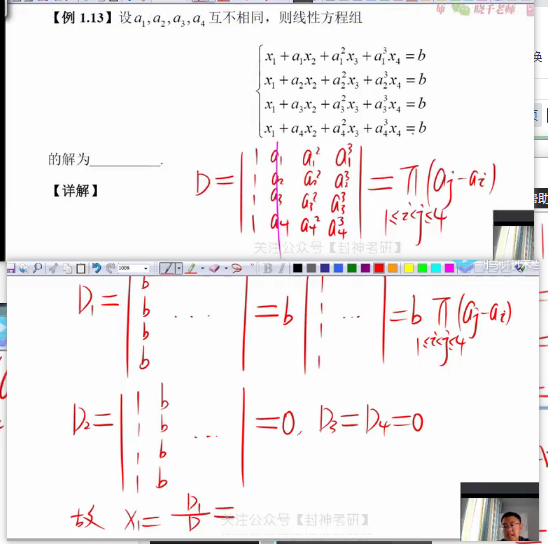
二.矩阵
矩阵的基本运算





lt
矩阵的逆

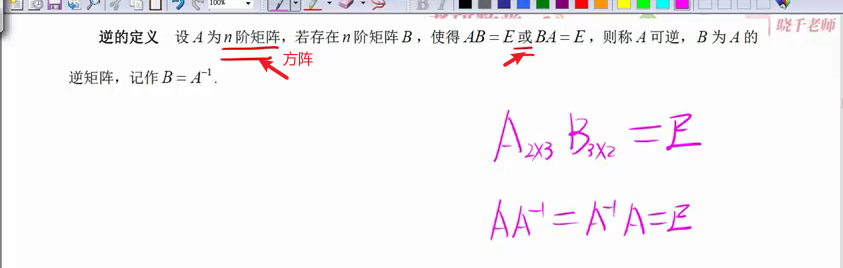
lt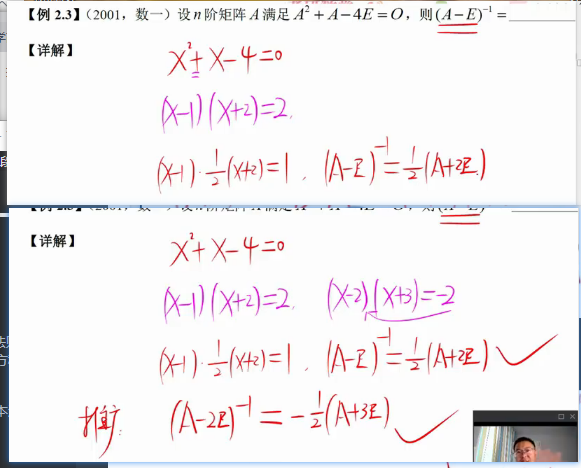
逆的性质:

lt 法1 定义
lt 2 法2 · 性质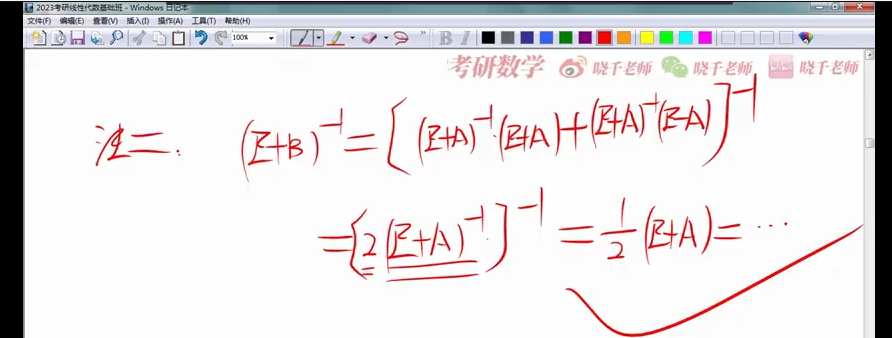
充要条件:充要
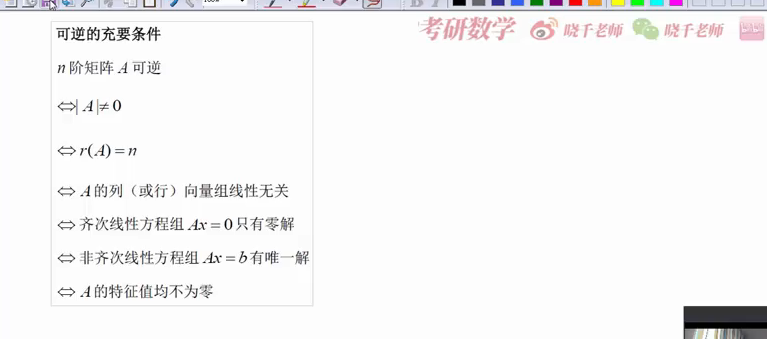
逆的两种求法

矩阵的秩
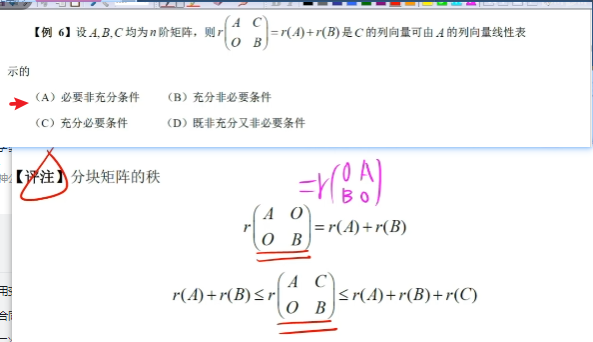
lt:但是本题如果改成了A可逆的话,这就是充分必要条件了
https://www.bilibili.com/video/BV1Sd4y1r7pw/?spm_id_from=333.337.search-card.all.click&vd_source=f802128dc44c00ca4c4a47ece8d1f3dd
第三个等于我们可以从极大无关组角度去理解,因为A可逆方阵(那么本身就是极大无关组),所以下面的和右面的都可以被她表示,也就是可以被消去
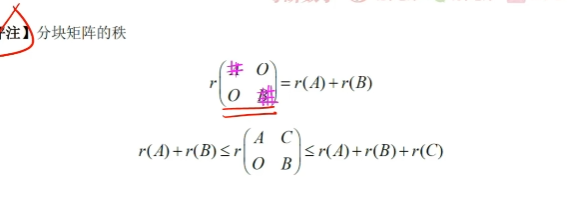
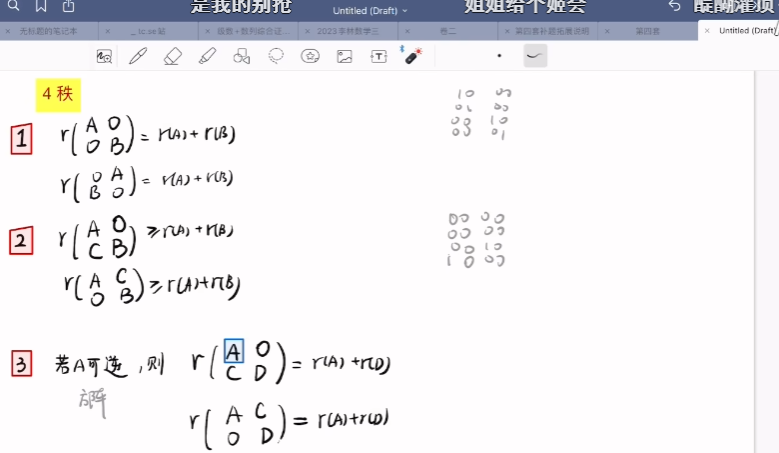
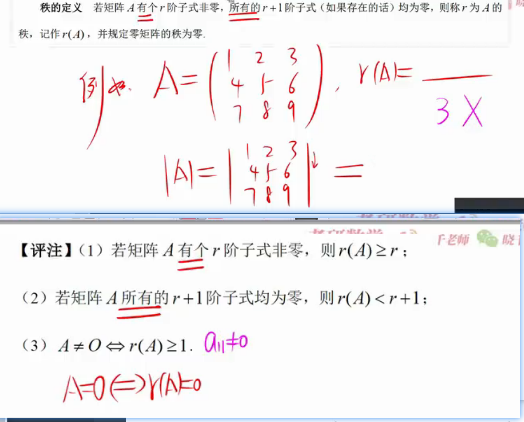
行满秩:
T1

第8个乘以转置矩阵秩不变,这里AtA等于AAt是因为判断秩才满足交换律,但是一般A的转置A并不等于A乘以A的转置,只有当正交的时候才满足交换律
秩的性质:9条 最重要的
记忆技巧 2349都是AB两个矩阵,15678都是单独的A的矩阵(倍乘、乘以列行满秩)
第四个:联立拼接的秩大于等于每一个,小于等于秩的和
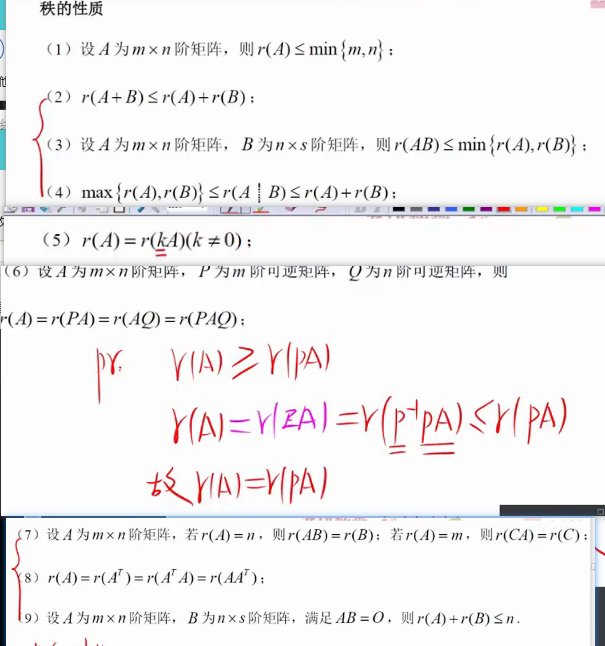
t 1
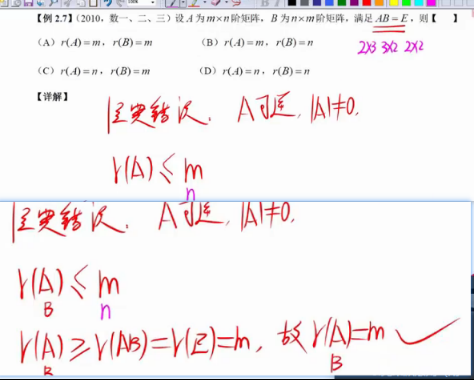
t2 

秩的求法:最重要
定义、 化为行阶梯形
伴随矩阵

定义、性质8条


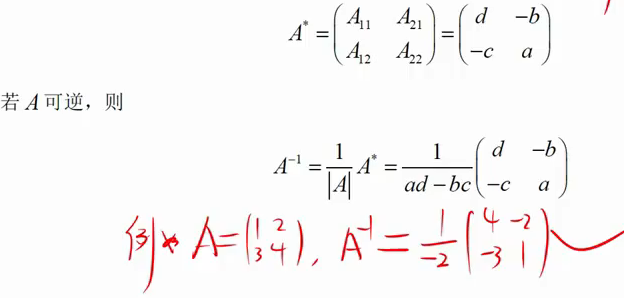
只是二阶使用:二阶的行列式是ad-bc,二阶的伴随是主对角线交换 副对角线添加负号
重要:伴随矩阵公式

一旦我们求A*卡住了,我们就求A逆乘以A的行列式

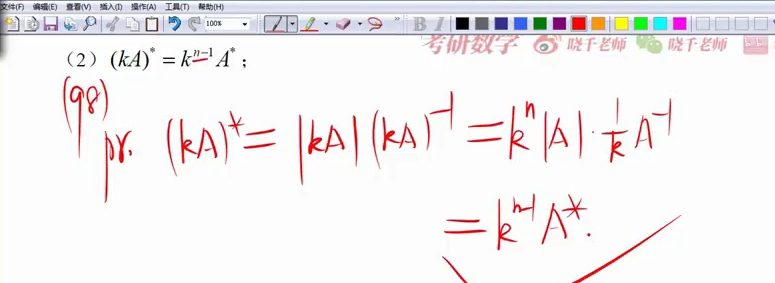
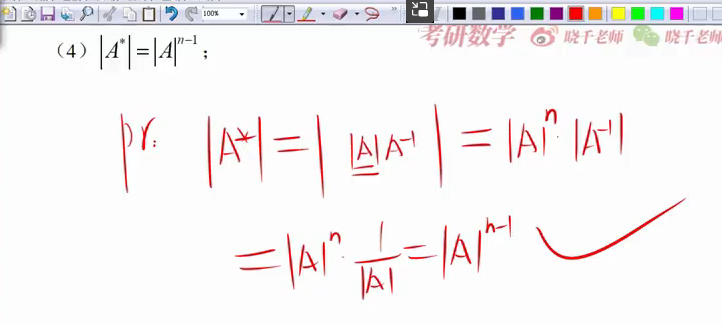
线性代数只有3个n-1,上面占了2个,还有一个是ab型行列式
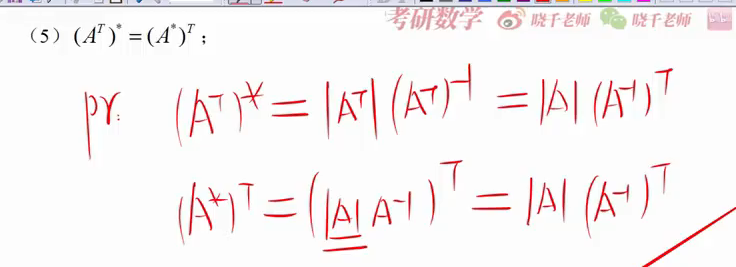
重要 A的逆的*等于行列式分之A的


矩阵乘法不满足交换律,所以因式分解对矩阵不能用
重要:星的星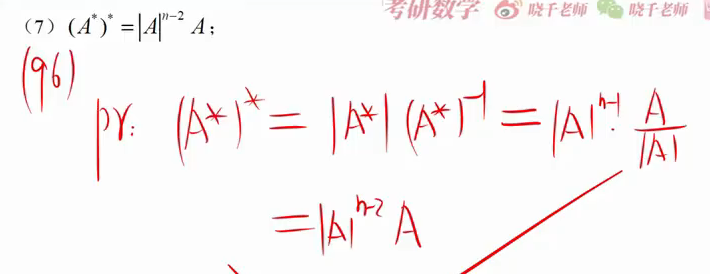
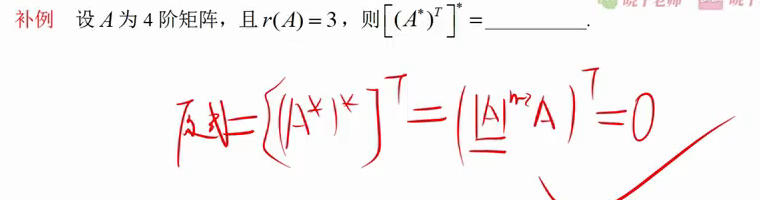
星的秩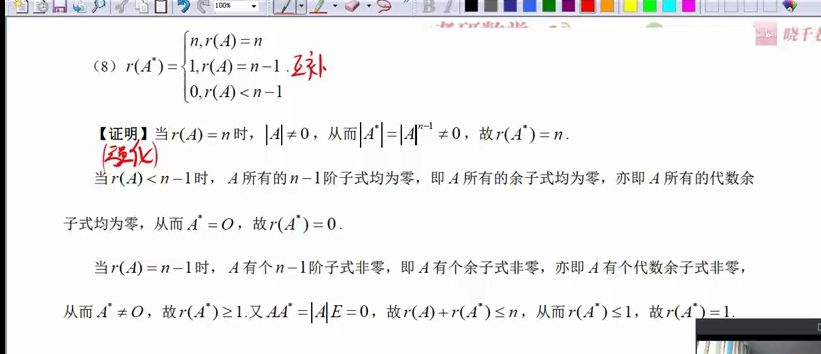
t1 子式是对行列式说的

矩阵的初等变化与初等矩阵
初等矩阵必须是一次初等变化
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-aFlxezaz-1690039595919)(https://gitee.com/jianwanxiansheng/cloudimage/raw/master/img/202307222320517.png)]
从后往前用行说,从前往后用列说
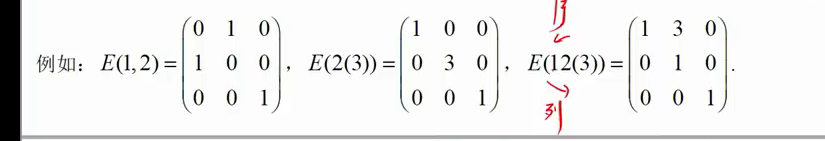
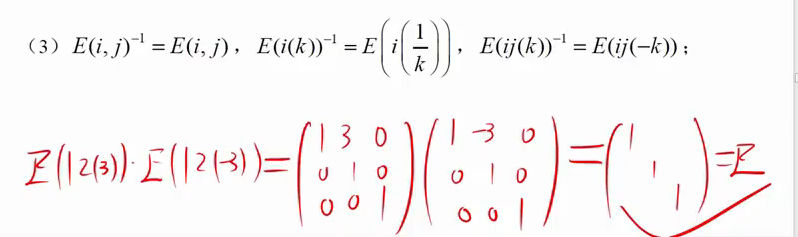
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-fdEcQspN-1690039595920)(https://gitee.com/jianwanxiansheng/cloudimage/raw/master/img/202307222320520.png)]
t1[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-VW8MiAeW-1690039595921)(https://gitee.com/jianwanxiansheng/cloudimage/raw/master/img/202307222320521.png)]
t2
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-wRvUJWEy-1690039595922)(https://gitee.com/jianwanxiansheng/cloudimage/raw/master/img/202307222320522.png)]
应用:
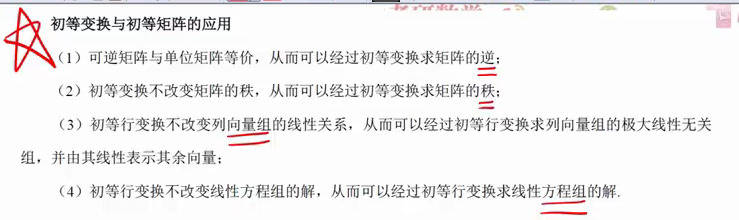
矩阵等价的充要条件
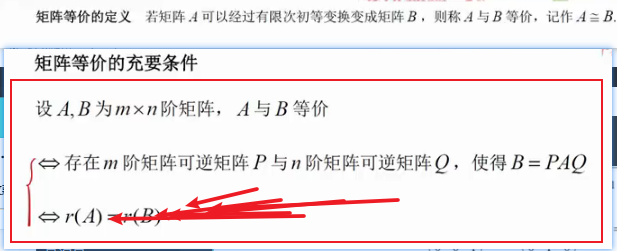
t1
法1 最好是不要用定义,法1是用的第一个充要条件
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-J7s922rk-1690039595925)(https://gitee.com/jianwanxiansheng/cloudimage/raw/master/img/202307222320525.png)]
法2 我们注意将秩和行列式联系起来 法2是用的第2个充要条件
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-6UcPfsrI-1690039595926)(https://gitee.com/jianwanxiansheng/cloudimage/raw/master/img/202307222320526.png)]
t2 法1是用的第2个充要条件
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-M1sdptnv-1690039595926)(https://gitee.com/jianwanxiansheng/cloudimage/raw/master/img/202307222320527.png)]
分块矩阵
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-F3p4sDCG-1690039595937)(https://gitee.com/jianwanxiansheng/cloudimage/raw/master/img/202307222320528.png)]
涉及到分块矩阵的加法,数乘,乘法,行列式(就是拉普拉斯)、转置、逆、伴随
分块矩阵其实就是二阶的对角矩阵,我们可以把任意的主对角线的矩阵分块成二阶的矩阵来求逆,这样方便求逆
此外:对角矩阵的逆矩阵就是对角线取倒数,不管她是几阶的对角矩阵


而对于一般的二阶矩阵来说,它的逆矩阵等于副对角线添加符号(而分块矩阵的副对角线相比二阶的矩阵的来说,除了添加负号还要交换位置),主对角线是好多分之一
推广
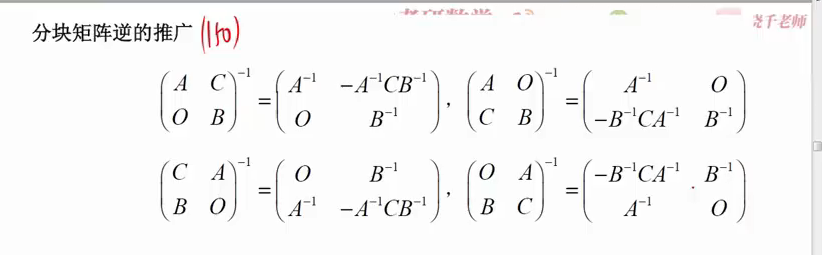
分块矩阵的行列式就是拉普拉斯(上三角、下三角、主对角、副对角,其中副对角有个-1的mn次方)
注意:初等矩阵的逆才是用的那个行互换,矩阵不变;;
而对于一般的二阶矩阵来说,它的逆的矩阵等于副对角线添加符号
t1 分块矩阵的行列式就是拉普拉斯(上三角、下三角、主对角、副对角,其中副对角有个-1的mn次方)
涉及到分块矩阵的加法,数乘,乘法,行列式(就是拉普拉斯)、转置、逆、伴随
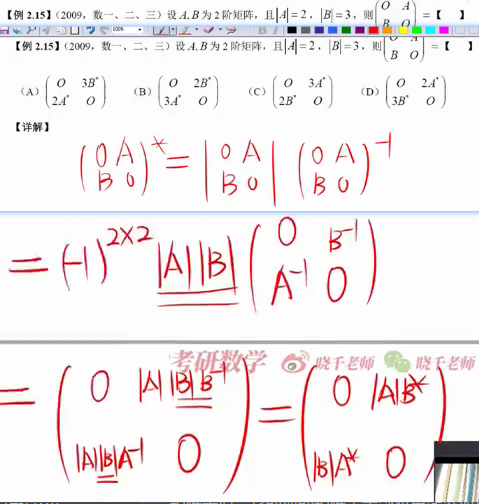
二阶矩阵的伴随和分块矩阵的对比
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-BuR4trJk-1690039595941)(https://gitee.com/jianwanxiansheng/cloudimage/raw/master/img/202307222320534.png)]
正交矩阵

正交矩阵的话,A的转置一定是等于A逆的
https://www.bilibili.com/video/BV1eJ411N7Qr/?spm_id_from=333.337.search-card.all.click&vd_source=f802128dc44c00ca4c4a47ece8d1f3dd

三.
向量的基本运算

重要:
内积是一行乘以一列,长度是根号下平方和
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-xkMKO45H-1690039595942)(https://gitee.com/jianwanxiansheng/cloudimage/raw/master/img/202307222320538.png)]
性质:数乘只能乘以-1,不能是2 3 啥的
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-B6MIMXS1-1690039595942)(https://gitee.com/jianwanxiansheng/cloudimage/raw/master/img/202307222320539.png)]
t1 为什么转置行列式不变呢,因为行列互换行列式的值是不变的


施密特正交化:
线性表示
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-n9ZZRVc0-1690039595944)(https://gitee.com/jianwanxiansheng/cloudimage/raw/master/img/202307222320544.png)]
向量组等价:三秩相等
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ljWocJhF-1690039595944)(https://gitee.com/jianwanxiansheng/cloudimage/raw/master/img/202307222320545.png)]
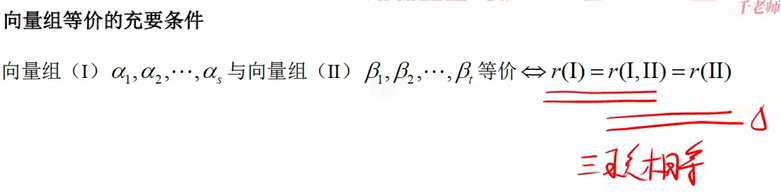
向量组等价:
证明向量组等价的3种方法:
1定义:可以互相相互线性表示
2.三个秩序A B 和AB联立的秩相等
3证明了2个秩相等和一个可以被线性表示也可以说明

法1 
法2 初等矩阵的乘积和分块矩阵[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-bdJUcnRI-1690039595946)(https://gitee.com/jianwanxiansheng/cloudimage/raw/master/img/202307222320549.png)]
线性表示的充要条件:

类比矩阵等价:相似一定等价,但是等价不一定相似,因为矩阵等价只是保证了同型的矩阵秩是相等的
向量组等价:三秩相等
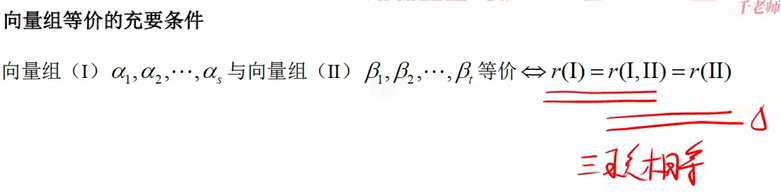
秩重要(第一张的行列式等不等于0,第二章的矩阵是否等价(是否可逆),第三章线性表示和向量组等价和相关无关,还有齐次非齐次,特征值特征向量,二次型)

充分条件:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-2yMmFOZh-1690039595948)(https://gitee.com/jianwanxiansheng/cloudimage/raw/master/img/202307222320552.png)]
t
t1[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-dcStkX1Y-1690039595948)(https://gitee.com/jianwanxiansheng/cloudimage/raw/master/img/202307222320553.png)]
线性相关与线性无关1
高维相关,则低维相关


t
t1[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-rVLrEz0Z-1690039595951)(https://gitee.com/jianwanxiansheng/cloudimage/raw/master/img/202307222320556.png)]
t2 线性相关无关的证明:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-E9G0wliT-1690039595951)(https://gitee.com/jianwanxiansheng/cloudimage/raw/master/img/202307222320557.png)]
线性相关与线性无关2
线性相关的充要条件(3个):
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-oxJlKXFM-1690039595952)(https://gitee.com/jianwanxiansheng/cloudimage/raw/master/img/202307222320558.png)]
推论:行列式和可逆必须要求是方阵
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-yFemh4ED-1690039595952)(https://gitee.com/jianwanxiansheng/cloudimage/raw/master/img/202307222320559.png)]
类比线性表示的充要条件2个:1.非齐次方程组有解 2. 系数矩阵的秩等于增广矩阵的秩
lt
t1 定义
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-fnBDuO0r-1690039595953)(https://gitee.com/jianwanxiansheng/cloudimage/raw/master/img/202307222320561.png)]
法2 行列式 因为他是n*n的,所以用那个推论的充条件
也可以用秩,秩为1《3[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-KghC8dcH-1690039595954)(https://gitee.com/jianwanxiansheng/cloudimage/raw/master/img/202307222320562.png)]

线性相关的充分条件:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Zl6sN1iU-1690039595954)(https://gitee.com/jianwanxiansheng/cloudimage/raw/master/img/202307222320564.png)]
无关的充分条件:无关被表 个数不多
线性相关充分条件:以少表多,多必相关
lt
线性无关的充要条件(3个):
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-iJkMEDqs-1690039595955)(https://gitee.com/jianwanxiansheng/cloudimage/raw/master/img/202307222320566.png)]
线性无关的充分条件:(线性相关充分条件的逆否)
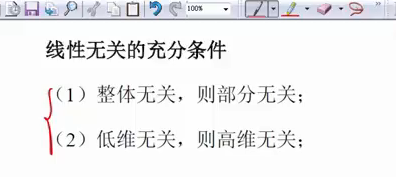
重要[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-4joyYLIy-1690039595956)(https://gitee.com/jianwanxiansheng/cloudimage/raw/master/img/202307222320568.png)]
lt 
法1 A用定义

极大线性无关组与向量组的秩
考点:矩阵的秩等于列向量组的秩,是极大无关组的列向量个数(向量组核心想极大无关组,方程组核心----------以下这是线性相关和无关的充分条件:无关被表 个数不多 逆否命题是以少表多,多必相关 这两个只是线性相关和无关的充分条件
极大无关组就是线性无关的列向量的个数
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Plp3xcAQ-1690039595957)(https://gitee.com/jianwanxiansheng/cloudimage/raw/master/img/202307222320571.png)]

秩的定义:行阶梯型非0行的行数,就是矩阵的秩
矩阵的秩行向量组和列向量组的秩
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Q1hR5ske-1690039595958)(https://gitee.com/jianwanxiansheng/cloudimage/raw/master/img/202307222320573.png)]
有的时候矩阵的秩不好做,就转换成第三章向量组的秩(向量组的秩也就是极大无关组的个数),反过来,向量组也可以转换成矩阵
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-VWSMCP3E-1690039595958)(https://gitee.com/jianwanxiansheng/cloudimage/raw/master/img/202307222320574.png)]

lt
t1

初等行变化变成行阶梯型,就能得到极大无关组,化为行最简型,就能线性表示

四.
线性方程组



系数和为1和0
基础解析我们需要的是线性组合系数和是0的,也就是齐次的特解解,加上k就是齐次的通解了 特解我们是要求系数和为1
+2重要:非齐次方程组的线性组合有2种情况,得看系数和

非齐次方程组线性无关得解 重要
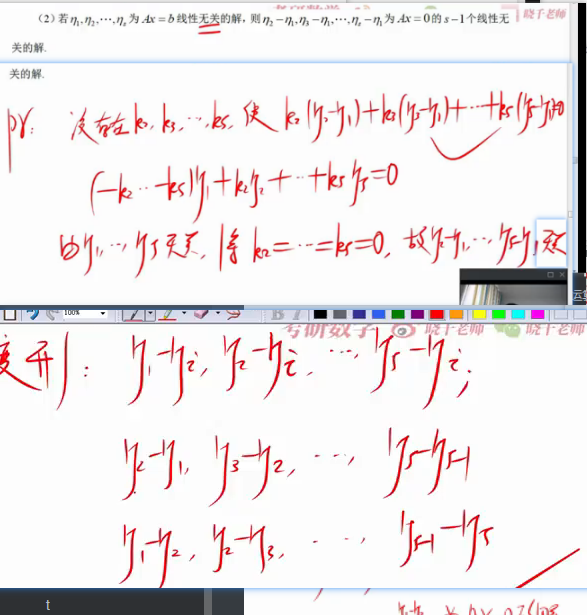
t
t1 由性质1:齐次的线性组合,和线性表示的充要条件(看增广矩阵的秩和系数矩阵的秩)
sl:将他的性质也就是必要条件,他的线性组合的解也一定是齐次的解,然后将这个线性组合的解转化到线性表示这里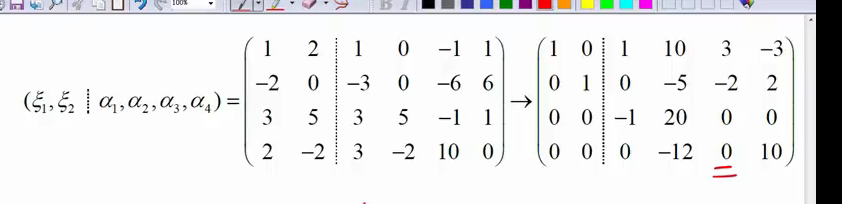
=
齐次方程组解的判定
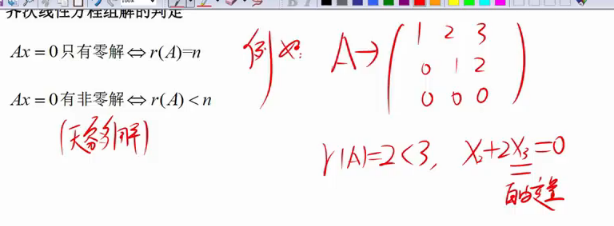

t
t1
=

矩阵的秩等于(列)向量组的秩,而向量组的秩又是极大无关组向量的个数
t1
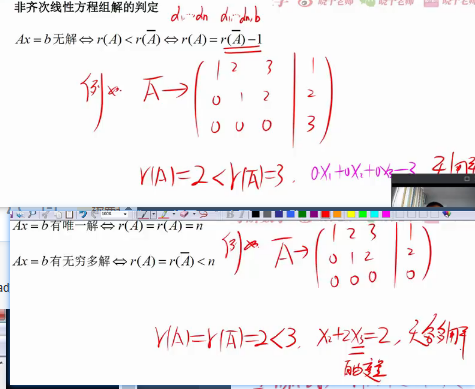
推论:行满秩就是秩等于行数

重要:非齐次方程组上来是要先看增广矩阵的秩等于系数矩阵的秩,在判断是否小于列数n
t
本题实际就是看秩,而秩呢实际上就是将矩阵化为行阶梯型然后看非0行的行数

齐次线性方程组1
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-sJ0n9oVB-1690039595967)(https://gitee.com/jianwanxiansheng/cloudimage/raw/master/img/202307222320594.png)]
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-9sVn1kEd-1690039595968)(https://gitee.com/jianwanxiansheng/cloudimage/raw/master/img/202307222320595.png)]
t
综合题
sl:解 有线性组合的性质 == 秩的性质 左乘列满秩,秩不变

t2
本题第二问证明的是秩的第九条性质

齐次线性方程组2
利用定义来求抽象矩阵的解的时候,必须要求有非齐次方程组
求秩只需要化成行阶梯型,但是求基础解析和线性表示的时候,一定要化成行最简型
t
t1
若A*B=0,则B的每一列都是A这个方程组的解

=

t
抽象矩阵
解法2步骤:1 求ra,也就是n-ra,第二部是利用解的定义(2类)或者性质(2条 非齐次的)来凑这n-ra个解
利用定义来求抽象矩阵的解的时候,必须要求有非齐次方程组 本题没有
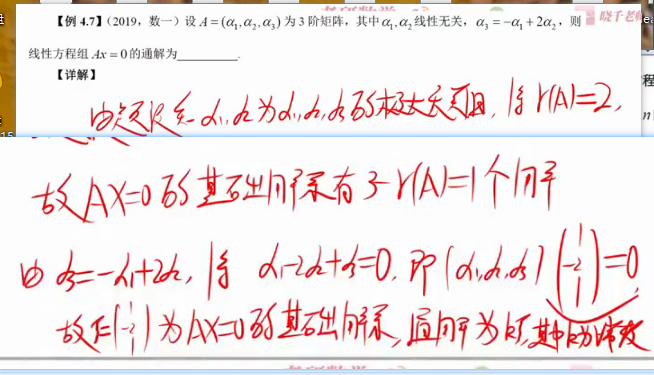
t2 数字矩阵
sl:初等行变换化成行最简型 利用秩的性质九

非齐次线性方程组

t
本题抽象矩阵,利用解的定义或者性质

t2 数字矩阵的

公共解

== 有三个
t
这里只是讨论的a这一个参数。所以a每次讨论的时候只能取一个值
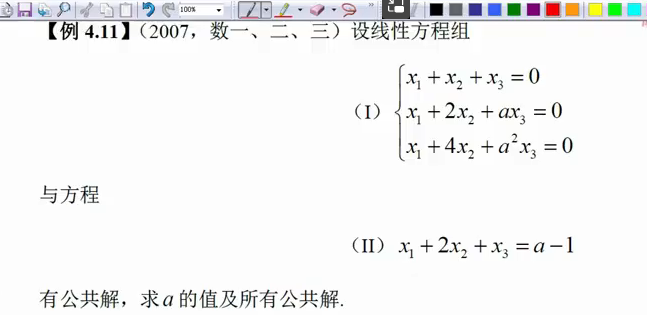
基础解析克赛不带k为任意常数
同解
区分向量组等价的充分条件:三秩.相等(他是列向量组联立)
而同解是行向量组联立,
注意:同解对象 这里给的AB是矩阵,而向量组等价是给的列向量组

 向量组等价和方程组同解 都有三秩相等,只不过向量组等价是左右联立,而方程组同解是上下联立
向量组等价和方程组同解 都有三秩相等,只不过向量组等价是左右联立,而方程组同解是上下联立
t
t1 证明了秩的性质8
难题都得利用矩阵的基本运算化简(有加法、数乘、转置)
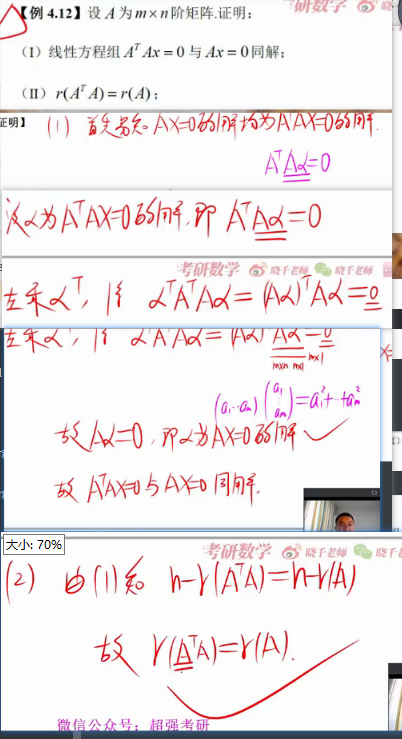
t2


五
特征值与特征向量的概念1
xx


zy
t
t1
定义:
t2 定义:

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-SS8UH5AI-1690039595977)(https://gitee.com/jianwanxiansheng/cloudimage/raw/master/img/202307222320621.png)]
=
特征方程发3步骤

==
推论:注意推论

t
t1
==正交矩阵充要条件有行列式为+1或者–1
正交矩阵有个隐含条件就是行列式为1或者-1

这里只要说了是正交矩阵,则我们构造A+E的行列式,并且化简,然后利用正交矩阵A的行列式不为0这个隐含条件,来推正交矩阵隐含的那个特征值,注意这里只有A的行列式小于0才有这个结论,大于0没有
特征值与特征向量的概念2
同一特征值的特征向量可能线性相关,但是要想让这个矩阵相似于对角矩阵,那么就必须要求同一特征值的特征向量是线性相关的



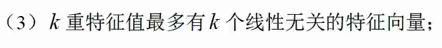
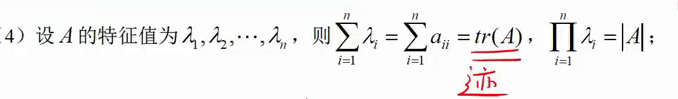

你行转世啊
t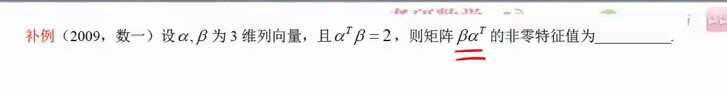

==
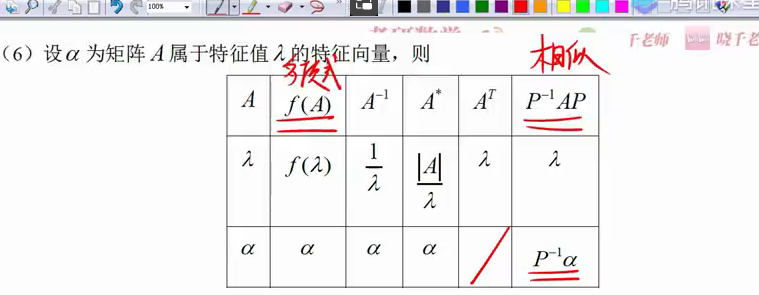
特征值和特征向量的表格法
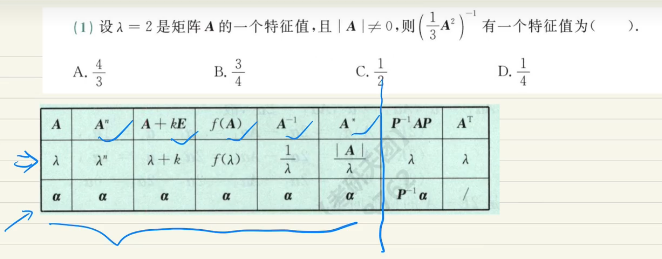
不同特征值的特征向量一定是不同的,但是同一特征值的特征向量可能相同可能不同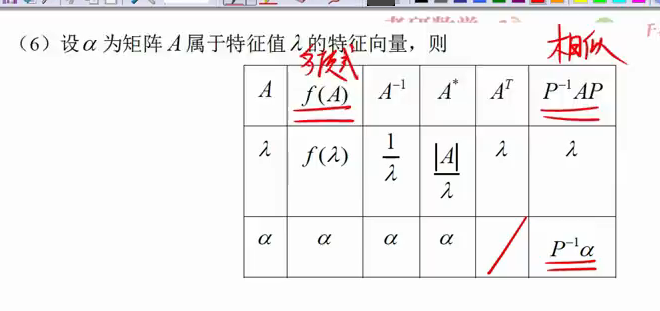

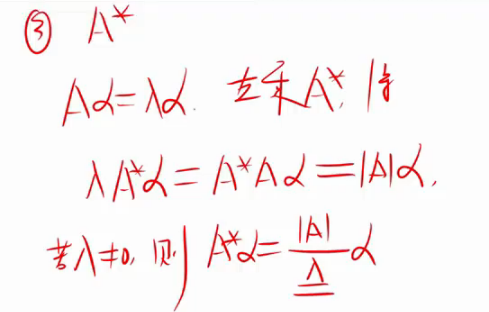
A的转置和A只是特征方程相同,故那慕达相同,但是特征向量无法确定
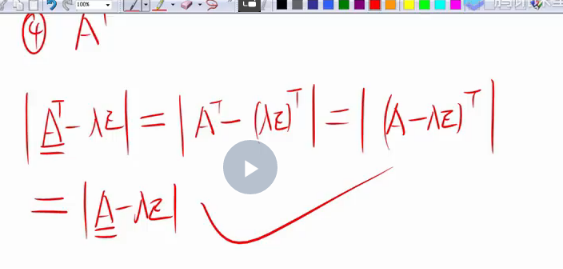
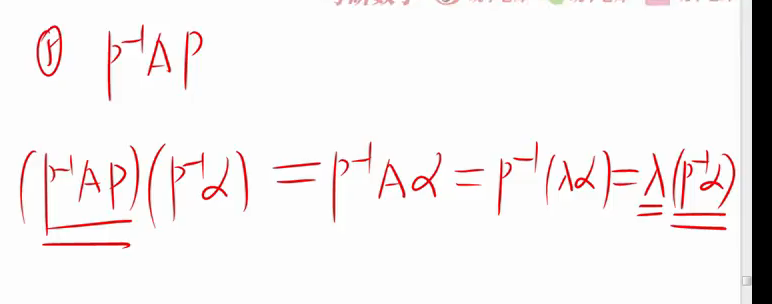
=

t

相似
矩阵相似一定等价,但是矩阵等价不一定相似

证明逆和转置

t
t1 逆是可以提出来的,转置不可以提

t2 本题考察相似和4个必要条件的当中的一个,特征值相同

相似对角化
只有相似对角化的矩阵秩等于非0特征
zj:只有这里才会求不同特征值的特征向量,然后拼接特征向量P和 相似的特征值矩阵


AB相似一定有相同的特征值,但是有相同的特征值不一定相似
特殊的,对于如果AB都是可以相似对角矩阵的,那么相似一定有相同的特征值,而且有相同的特征值也就一定相似 :::证明如下图


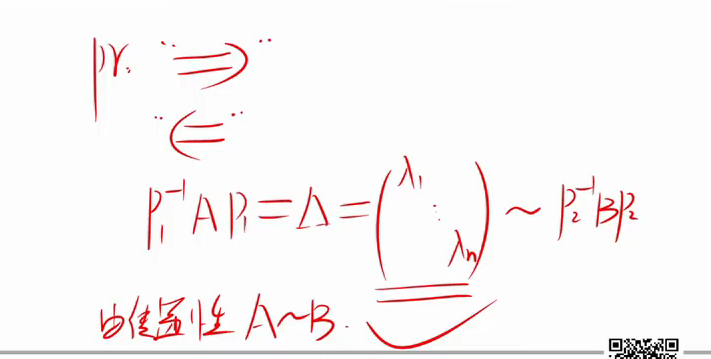
= 二充要 + 一个秩为1的充要
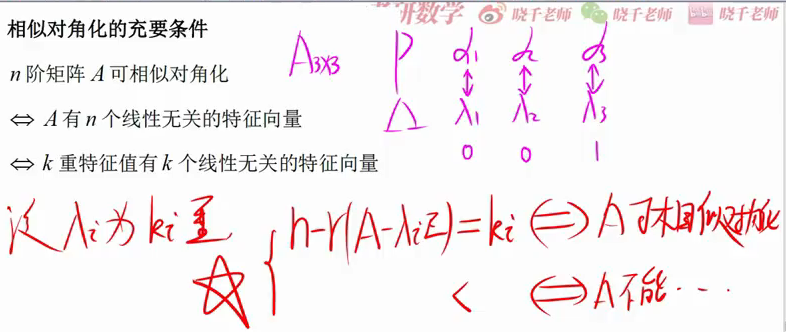
这里扩展一个特殊的当秩为1的矩阵可以相似对角化的充分必要条件是寄非0
t
判断相似除了四个必要条件,还有个他们共同相似于对骄矩阵
利用充要条件做

=
充分条件3个
三充分 二充要 + 一个秩为1的充要
充要补充1:还多了一个秩为1的矩阵,且迹不为0,也是充分条件(充要条件)则一定可以相似对角化
充分补充2:若特征方程

反例: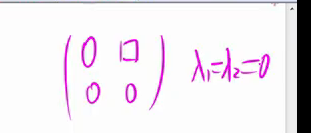
t2
可以通过秩等于非0特征值的个数来确定我们求出来的各个特征值有多少个
我们同时乘以一个阿尔法,A方阿尔法是那慕达平方倍阿尔法,A倍阿尔法是那慕达倍阿尔法,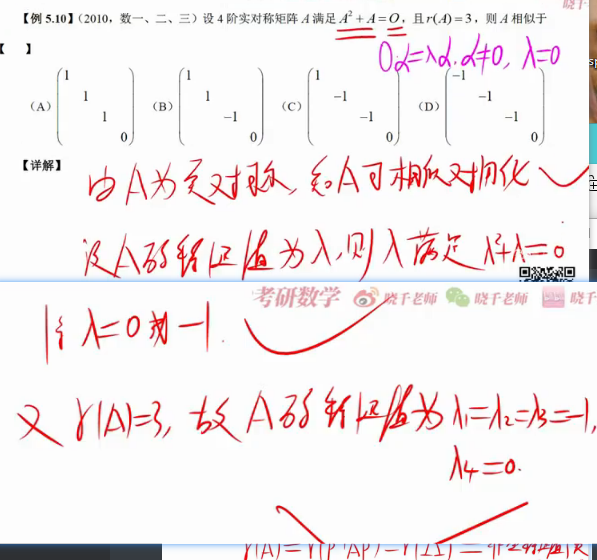
实对称矩阵
相似对焦的矩阵(除了实对称矩阵–它天生可以相似对角化)不同特征值的特征向量无关,而实对称矩阵不同特征值的特征向量不仅无关还正交
实对称矩阵的考点:不同特征值的特向是正交的
二:实对称矩阵的分解定理

实对称矩阵补充一个性质:天生存在一个对角矩阵和她相似
实对称矩阵的k重特征值一定是k个线性无关的特征向量,所以他必可相似对角化

正交是内积为0,长度为1

t
t1 利用推论,相似对角化的矩阵,秩等于非0特征值的个数
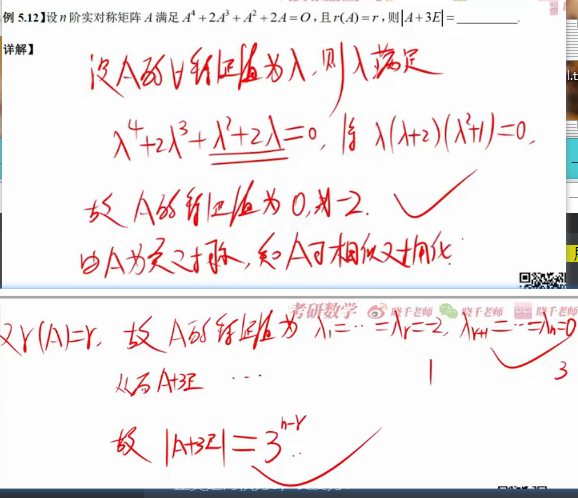
= 正交矩阵的3大步
只需要同一特征值的特征向量是正交的,即只需要同一特征值不同特征向量用正交化,然后单位话;;;;;同一
zzz 分解定理强化用
在05.第五章 专题四 实对称矩阵

t
t1
法1
因为本题是不知道A的具体矩阵,只知道他的两个正交的特征向量,但是不单位的,所以我们在求另外一个特征值的
A的秩是2,肯定有个那慕达是0

法2 只需要不同特征值的特征向量是正交的,同一特征值的向量不需要,因为同一特征值保证了特征向量一定是正交无关的,只需要单位化即可
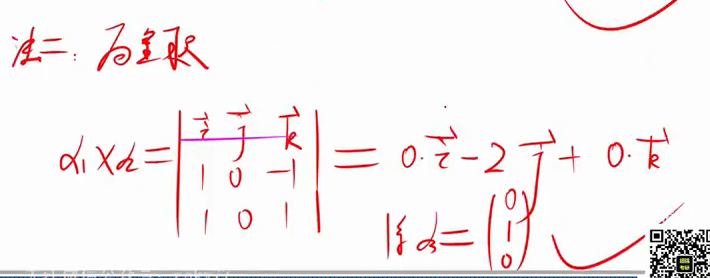
(2)
法3 A是用的分解定理,A秩为2,所以分解两次
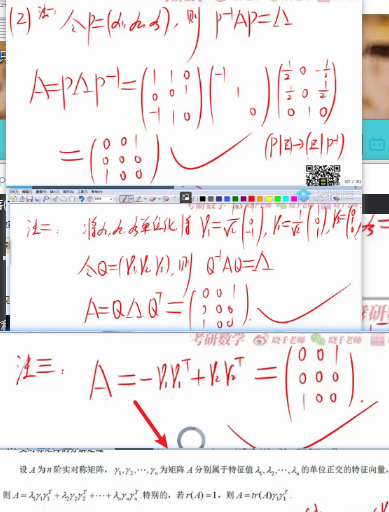
六.(这一章的矩阵都要求是实对称矩阵)
考点:拉格朗日配方法配出来虽然不一定满足是系数就是特征值,但是它可以保证的是拉格朗日配方法一定是可逆线性变换的
和其正 合同 正定
施密特正交化:
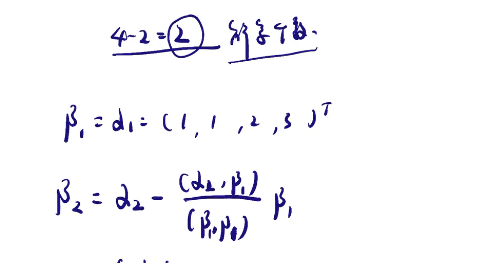
二次型与标准型
二次型的矩阵形式:


t

= 正交矩阵的转换的推导
先是标准型,再是规范型
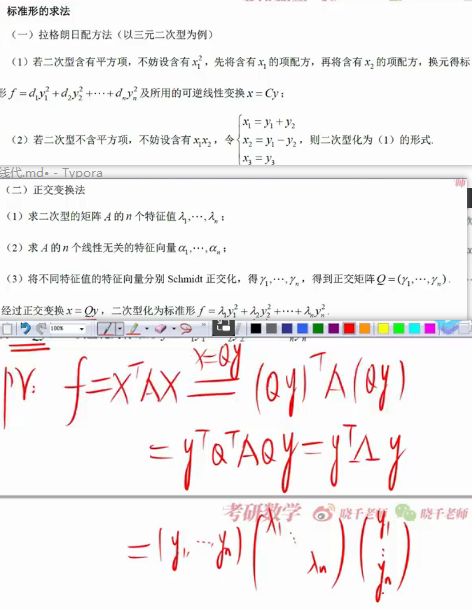
合同矩阵


充要条件 2个:巧记忆:合同合同,肯定要有相同的惯性指数和那慕达(合同合同 马同什么 ,同惯性指数和那慕达)
合同的充分条件::::在满足AB两个是实对称矩阵的前提下,AB相似是可以推出合同的
合同的必要条件:合同秩一定是相等的,反过来秩相等不一定合同 这是合同的必要条件
考点:合同变换包含了正交变换,因为合同变换是只是要求找到一个可逆的矩阵,并不需要找一个正交矩阵。
考点:相似变换的矩阵和合同变换的矩阵是必须要要求这个矩阵是可逆的
考点:正交变换既是合同 变换也是相似变换
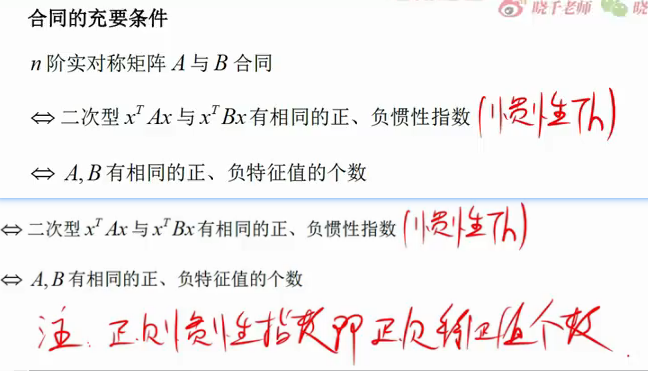
拓展:合同秩一定是相等的,反过来秩相等不一定合同 这是合同的必要条件
考点:合同变换包含了正交变换,因为合同变换是只是要求找到一个可逆的矩阵,并不需要找一个正交矩阵。
合同的充分条件::::在满足AB两个是实对称矩阵的前提下,AB相似是可以推出合同的
相似一定矩阵等价(因为相似的必要条件是秩相等),矩阵等价但是不一定相似
t 看合同只需要正负惯性指数

正定矩阵

=
正定的充要条件从特征值这里散发开可以得到3个,然后再来个和单位矩阵和合同,因为合同的必要条件是秩相同,因为E是满秩,所以正定矩阵一定是满秩矩阵
正定矩阵的必要条件:满秩、行列式不为0,还有必要条件就是主对角线的每个元素必须要大于0
考点必要条件;正定矩阵的主对角线元素一定大于零 逆否命题就是 主对角线元素有<零的就不正定


t

t2
相似、正定都满足上标运算的性质
(img-7qqNNK5o-1690039596007)]
[外链图片转存中…(img-BQhKiNU0-1690039596008)]
充要条件 2个:巧记忆:合同合同,肯定要有相同的惯性指数和那慕达(合同合同 马同什么 ,同惯性指数和那慕达)
合同的充分条件::::在满足AB两个是实对称矩阵的前提下,AB相似是可以推出合同的
合同的必要条件:合同秩一定是相等的,反过来秩相等不一定合同 这是合同的必要条件
考点:合同变换包含了正交变换,因为合同变换是只是要求找到一个可逆的矩阵,并不需要找一个正交矩阵。
考点:相似变换的矩阵和合同变换的矩阵是必须要要求这个矩阵是可逆的
考点:正交变换既是合同 变换也是相似变换
[外链图片转存中…(img-uEbJnvEW-1690039596008)]
拓展:合同秩一定是相等的,反过来秩相等不一定合同 这是合同的必要条件
考点:合同变换包含了正交变换,因为合同变换是只是要求找到一个可逆的矩阵,并不需要找一个正交矩阵。
合同的充分条件::::在满足AB两个是实对称矩阵的前提下,AB相似是可以推出合同的
相似一定矩阵等价(因为相似的必要条件是秩相等),矩阵等价但是不一定相似
t 看合同只需要正负惯性指数
[外链图片转存中…(img-seAtO4kq-1690039596008)]
正定矩阵
[外链图片转存中…(img-FIuJXxMj-1690039596009)]
=
正定的充要条件从特征值这里散发开可以得到3个,然后再来个和单位矩阵和合同,因为合同的必要条件是秩相同,因为E是满秩,所以正定矩阵一定是满秩矩阵
正定矩阵的必要条件:满秩、行列式不为0,还有必要条件就是主对角线的每个元素必须要大于0
考点必要条件;正定矩阵的主对角线元素一定大于零 逆否命题就是 主对角线元素有<零的就不正定
[外链图片转存中…(img-TXZPctNS-1690039596009)]
[外链图片转存中…(img-Q4r72nVR-1690039596010)]
t
[外链图片转存中…(img-gcTL7gLf-1690039596010)]
t2
相似、正定都满足上标运算的性质

本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!