MATLAB 作动态图
MATLAB 作动态图
- MATLAB 作动态图
- 动态线图
- 生成数据
- 作动态图
- 方法一
- 方法二
- 动态点图
- 确定参数
- 生成数据并创建函数句柄
- 迭代以形成动态效果
- 实际应用
- 输出效果
MATLAB 作动态图
本文谨记录笔者探索MATLAB作动态图后的心得,希望能帮到大家
动态线图
生成数据
首先打开MATLAB,生成一组数据。
以下是笔者在练习数学建模中的导弹追踪模型所写的一段代码
由于这段代码涉及的其他知识点较多,也不属于这篇文章的重点,有兴趣的读者可以看看,没有兴趣的可以用后文的替代代码
[x,y]=ode45(@df1,[0:1e-3:0.1],[20 0 0 0],[],200,45);distance=sqrt((y(:,1)-y(:,3)).^2+(y(:,2)-y(:,4)).^2);
length1=sqrt((y(2:end,3)-y(1:end-1,3)).^2+(y(2:end,4)-y(1:end-1,4)).^2);
length1=cumsum(length1);
choose=min(find(distance<=1e-1))-1;
length1(choose)plot(y(:,1),y(:,2),y(:,3),y(:,4),y(choose,1),y(choose,2),'bo',y(choose,3),y(choose,4),'ro')
% axis([0,max(y(:,1)),0,max(y(:,1))]function dy=df1(t,y,v,si)
% v=200;dy=zeros(4,1);dy(1)=cos(si/180*pi)*v;dy(2)=sin(si/180*pi)*v;dy(3)=3*v*(y(1)-y(3))/sqrt((y(1)-y(3))^2+(y(2)-y(4))^2);dy(4)=3*v*(y(2)-y(4))/sqrt((y(1)-y(3))^2+(y(2)-y(4))^2);
end
由于笔者使用的是实时脚本(听说是MATLAB 2016a之后才有),其可以使用局部函数,只需写在实时脚本最后即可。
而若使用普通脚本,则需在当前工作路径下新建函数文件,将其放入其中即可。
方便起见,使用普通脚本也可用下列代码代替
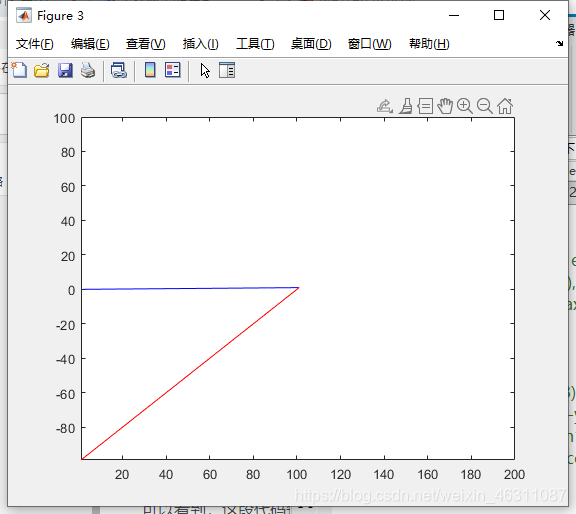
clear;clc
x=1:200;
y1=0.01*x;
y2=x-100;
y=[x;y1;x;y2]';
choose=100;
作动态图
方法一
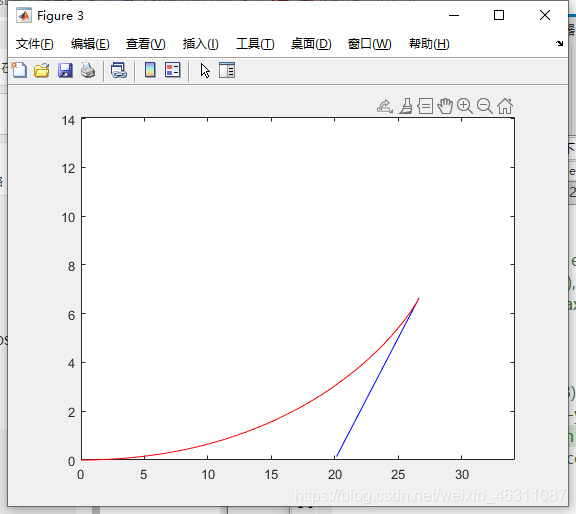
有了数据之后便可以开始作图了,以下便是作图代码
for i = 1 : chooseplot(y(i:i+1,1),y(i:i+1,2),'b','MarkerSize',1)plot(y(i:i+1,3),y(i:i+1,4),'r','MarkerSize',1)hold on axis([min(y(:,3)),max(y(:,3)),min(y(:,4)),max(y(:,4))]);pause(0.1)
end
可以看到,这段代码先是逐段画线,然后用hold on保持图像,用pause控制画线速度,用choose控制画线的终点,这里取的是两条线的交点。
方法二
实际上,在MATLAB 2016 及之后的版本,其新增了一个画动态线图的函数,使用起来比方法一要方便
| 函数方法 | 说明 | 输入参数 |
|---|---|---|
| animatedline | 创建动态线图的函数句柄 | (无输入参数) |
| addpoints(h,x,y) | 往动态线图新增点 | (动态线图的句柄,点的x坐标,点的y坐标) |
| getpoints(h) | 获取动态线图的所有点 | (动态线图的句柄) |
| clearpoints(h) | 清除动态线图的所有点 | (动态线图的句柄) |
h=animatedline;
axis([0 4*pi -1 1])
x=linspace(0,4*pi,1000);
y=sin(x);
for k = 1:length(x)addpoints(h,x(k),y(k));pause(0.01)
end
动态点图
确定参数
先确定几个参数
n = 10; % 粒子数量
K = 10; % 迭代的次数
vmax = [6 6]; % 粒子的最大速度
x_lb = [-15 -15]; % x的下界
x_ub = [15 15]; % x的上界
生成数据并创建函数句柄
然后笔者给出了一个实例函数,作出二维网格后计算出各点的值然后绘制出网格
其中 view([-39 45]) 是笔者认为可以较好展示此网格的角度
x1=x_lb(1):x_ub(1);
x2=x_lb(2):x_ub(2);
[x1,x2]=meshgrid(x1,x2);
y = x1.^2 + x2.^2 - x1.*x2 - 10*x1 - 4*x2 + 60;
mesh(x1,x2,y)
view([-39 45])
hold on
迭代以形成动态效果
然后迭代K次,给予一个随机数让点动起来,然后用一个for循环将点限制在绘图所在区域
然后利用函数句柄绘制散点图,即可动态展示散点
此处为了方便,用了一个函数(在实时脚本中放在最后即可,无需新建函数文件),也可用上一段代码的y来代替,其输出效果放在了实际应用后面
for d = 1:Kx=x-vmax+2*vmax.*rand(n,narvs);for i = 1:narvsx(x(:,i)<x_lb(i),i)=x_lb(i);x(x(:,i)>x_ub(i),i)=x_ub(i);endpause(0.5);h.XData=x(:,1);h.YData=x(:,2);h.ZData=Obj_fun1(x);
endhold offfunction y=Obj_fun1(x)y=x(:,1).^2+x(:,2).^2-x(:,1).*x(:,2)-10*x(:,1)-4*x(:,2)+60;
end
实际应用
这其实是笔者在写粒子群算法时想到的一种动态展示散点图的方式,以下是全部代码
%% 粒子群算法(最小值)
%% 设置粒子群算法的参数
n = 10; % 粒子数量
narvs = 2; % 变量个数
c1 = 2; % 每个粒子的个体学习因子,也称为个体加速常数
c2 = 2; % 每个粒子的社会学习因子,也称为社会加速常数
w = 0.9; % 惯性权重
K = 10; % 迭代的次数
vmax = [6 6]; % 粒子的最大速度
x_lb = [-15 -15]; % x的下界
x_ub = [15 15]; % x的上界%% 初始化粒子的位置和速度
x=x_lb+(x_ub-x_lb).*rand(n,narvs);
v=-vmax+2*vmax.*rand(n,narvs);%% 计算适应度
fit=Obj_fun1(x);
pbest=x;
ind=find(fit==min(fit));
gbest=x(ind,:); %% 画图
x1=x_lb(1):x_ub(1);
x2=x_lb(2):x_ub(2);
[x1,x2]=meshgrid(x1,x2);
y = x1.^2 + x2.^2 - x1.*x2 - 10*x1 - 4*x2 + 60;
mesh(x1,x2,y)
view([-39 45])
hold on
h=scatter3(x(:,1),x(:,2),fit,'*r');%% 更新粒子速度和位置
gbest_val_list=zeros(1,K);
for d = 1:Kv=w*v+c1*rand(n,narvs).*(pbest-x) ...+c2*rand(n,narvs).*(gbest-x);for i = 1:narvsv(v(:,i)<-vmax(i),i)=-vmax(i);v(v(:,i)>vmax(i),i)=vmax(i);endx=x+v;for i = 1:narvsx(x(:,i)<x_lb(i),i)=x_lb(i);x(x(:,i)>x_ub(i),i)=x_ub(i);endfit=Obj_fun1(x);pbest(fit<Obj_fun1(pbest),:)=x(fit<Obj_fun1(pbest),:);if sum(Obj_fun1(pbest)<Obj_fun1(gbest)) > 0gbest=pbest(Obj_fun1(pbest) == min(Obj_fun1(pbest)),:);endgbest_val_list(d)=Obj_fun1(gbest);pause(0.5);h.XData=x(:,1);h.YData=x(:,2);h.ZData=fit;
end%% 输出
hold off
plot(1:K,gbest_val_list)
disp('最优解坐标为:')
disp(gbest)
disp('最优解值为:')
disp(Obj_fun1(gbest))function y=Obj_fun1(x)y=x(:,1).^2+x(:,2).^2-x(:,1).*x(:,2)-10*x(:,1)-4*x(:,2)+60;
end
输出效果
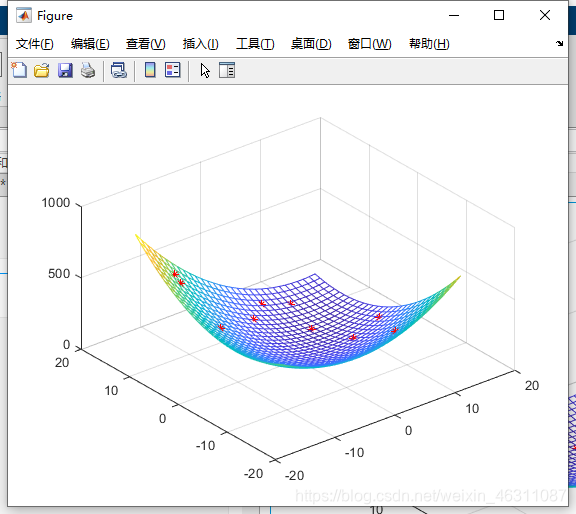
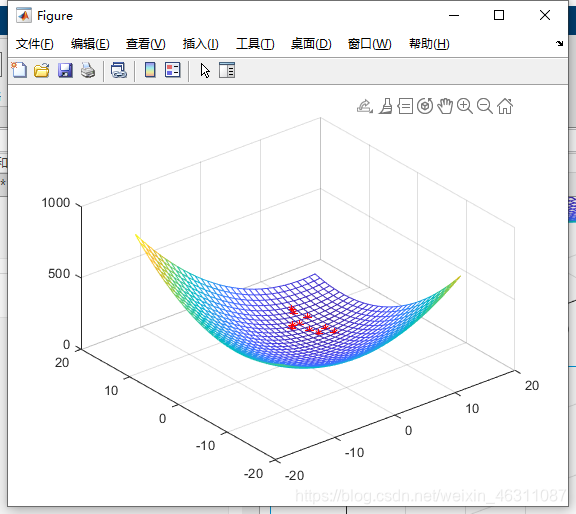
可以看到,这样的展示方式可以直观地看出粒子群算法寻找函数最小值的过程
本文到此结束,如有啥问题,可以留言告诉我哦
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!