【游戏课】技术片段之——球面线性插值（SLERP）

球面线性插值（Spherical linear interpolation，通常简称Slerp），是四元数的一种线性插值运算，主要用于在两个表示旋转的四元数之间平滑差值。（wiki）

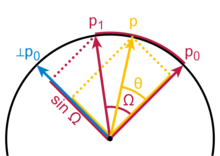
cos Ω = p₀ ∙ p₁

当Ω → 0时，退化为线性插值。

在Unity中，文档说明如下

Vector3.Slerp

static Vector3 Slerp(Vector3 from, Vector3 to, float t); Description

Spherically interpolates between two vectors.

Interpolates between  from and  to by amount  t. The difference between this and linear interpolation (aka, "lerp") is that the vectors are treated as directions rather than points in space. The direction of the returned vector is interpolated by the angle and its  magnitude is interpolated between the magnitudes of  from and  to.

t is clamped between [0...1]. See Also:  Lerp function.
C#代码如下

using UnityEngine;
using System.Collections;public class Example : MonoBehaviour {public Transform sunrise;public Transform sunset;public float journeyTime = 1.0F;private float startTime;void Start() {startTime = Time.time;}void Update() {Vector3 center = (sunrise.position + sunset.position) * 0.5F;center -= new Vector3(0, 1, 0);Vector3 riseRelCenter = sunrise.position - center;Vector3 setRelCenter = sunset.position - center;float fracComplete = (Time.time - startTime) / journeyTime;transform.position = Vector3.Slerp(riseRelCenter, setRelCenter, fracComplete);transform.position += center;}
}

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！