差分

作用： 用O(1)的时间复杂度完成对区间[l,r]加上c。
思路：如要完成对a数组中的区间完成次操作，则需要构造辅助数组b来完成，b数组的实际含义为 b的前缀和为a（a₃=b₁+b₂+b₃）。
例：一维差分

如何构造差分数组

构造差分数组在建立a数组时即可完成

for(int i=1；i<=n;i++)
{cin>>a[i] ; insert(i,i,a[i]);//相当于每次在i位置加上a[i]
}

如何完成区间加减

void insert(int l,int r,int c)//对区间[l,r]加上c
{b[l]+=c;b[r+1]-=c;
}

a数组的值即为b数组的前缀和

二维差分

作用： 用O(1)的时间复杂度完成对子矩阵加上c。
思路：假设对a数组(x1,y1)到(x2,y2)的子矩阵加上c，构造差分数组b对b数组的子矩阵操作，b数组的前缀和即为a数组值的大小（二维数组前缀和）。
例二维差分

构造二维差分数组

for(int i=1;i<=n;i++)for(int j=1;j<=m;j++){cin>>a[i][j];insert(i,j,i,j,a[i][j]);}

如何完成区间加减

void insert(int x1,int y1,int x2,int y2,int c)
{b[x1][y1]+=c;b[x1][y2+1]-=c;b[x2+1][y1]-=c;b[x2+1][y2+1]+=c;
}

a数组的值(二维数组的区间和)

a[i][j]=b[i-1][j]+b[i][j-1]-b[i-1][j-1];

位运算

求n的第k位数字：n>>k&1(下标从0开始）
返回n的最后一位1:lowbit(n)=n&-n

例：
x=10100 lobit(x）=100
x=101000 lobit(x)=1000
为什么：
-x=~x+1
例： x=10101000 ~x=01010111 ~x+1=01011000
~x+1&x=1000

例题(lobit的基本概念)

离散化

vectoralls;//存储所有待离散化的值
sort(alls.begin(),alls.end());将所有值排序
alls.erase(unique(alls.begin(),alls.end()),alls,end())//去掉重复元素
//二分找出对应离散化的值
int find(int x)
{int l=0,r=alls.size()-1;while(l>1;if(alls[mid]>=x) r=mid;else l=mid+1;}return l;
}

离散化例题

Tire树

Trie统计字符串

并查集

基本原理：每个集合用一棵树表示。树根的编号就是整个集合的编号。每个节点存储他的父节点，p[x]表示x的父节点。

如果是树根，则p[x]==x
求x的集合编号：while（p[x]!=x）x=p[x];
合并两个集合的编号：px是x的集合编号，py是y的集合编号。p[x]=y
优化：路径压缩。
查找祖宗节点

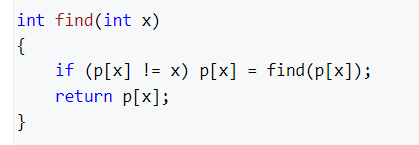
初始化

合并A,B集合

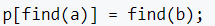
判断a，b是否在同一集合内
if( find(a)==find(b)

字符串哈希

（转载）



字符串哈希

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！