1. 复数矩阵

1. 对于复数向量来说，求膜长的时候要采用（根号 X H X X^HX XHX），也就是共轭转置，这样求出来的膜长才是符合真正需求的，而不是简单的转置。求内积也是如此。
2. 对于对称的定义也变成了共轭转置。
   
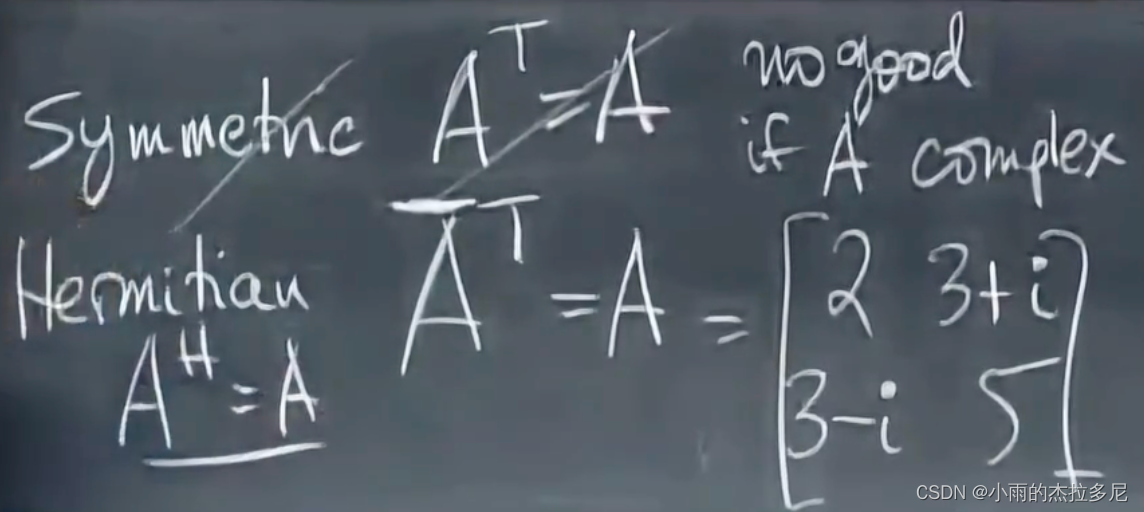
3. 正交矩阵也从任意两个向量共轭相乘判断，变为了H转置。此时组成的正交矩阵也被叫为酉矩阵（Unitary）。
   

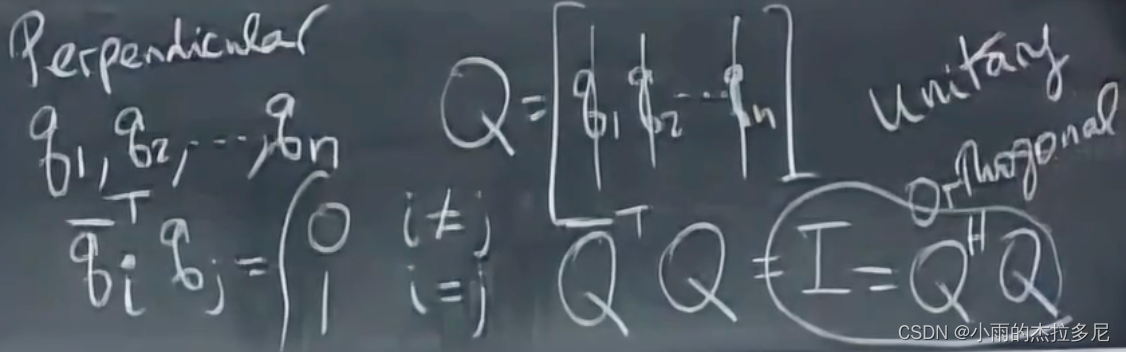
2. 傅立叶矩阵

傅立叶矩阵特点：是个全矩阵（没有零元素），并且是正交的
其中每一项都是 ( F n ) i j = w i j (F_n)_{ij} = w^{ij} (Fn​)ij​=wij

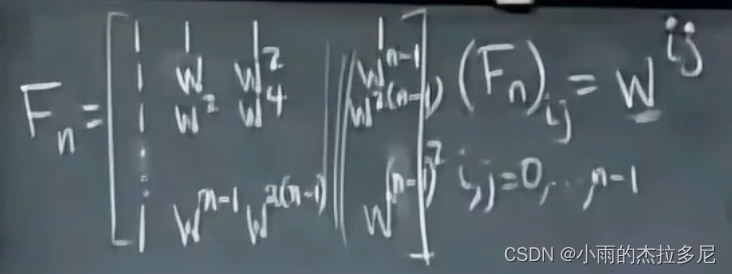
其中 w n = 1 w^n = 1 wn=1，即 w = e i ∗ 2 π / n w = e^{i*2\pi/n} w=ei∗2π/n， 每一个w都在单位圆上。

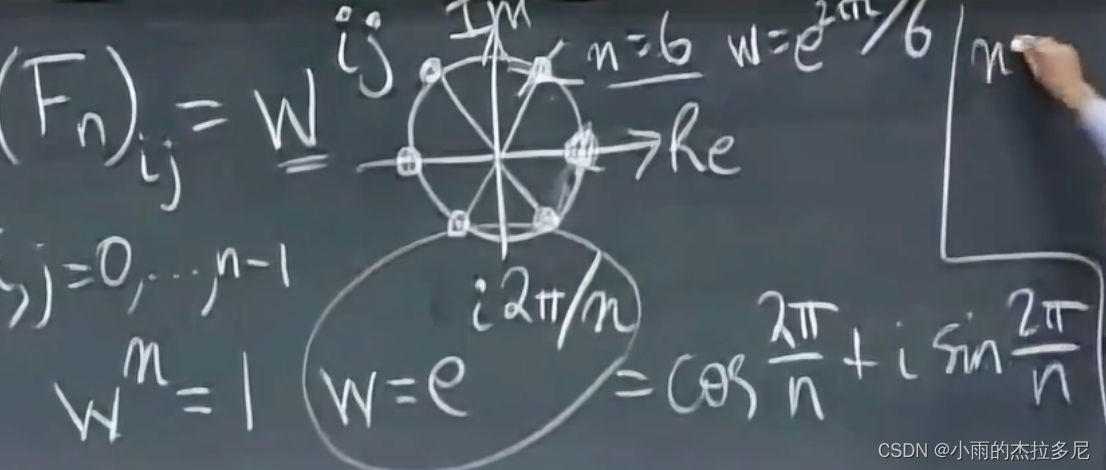
但是不是真的标准正交，而只是正交。因此要让 F n = 1 / n ∗ F n F_n=1/\sqrt{n} *F_n Fn​=1/n ​∗Fn​，这样他的逆就好求了。就是共轭转置

3. FFT（快速傅立叶变换）

可以观察到傅立叶中w有一些规律，比如 w 64 w_{64} w64​可以写作 w 32 2 w_{32}^2 w322​，因此可以简化运算。

具体的：
以n=64时为例， F 64 F_{64} F64​可以被分解为两个 F 32 F_{32} F32​的排列。以及左右乘两个矩阵。

1. 其中右侧是一个Permutation置换矩阵，作用就是把所有的偶数项换到前边（从0开始），奇数项放后边，这个计算可以忽略。
2. 左侧的对角矩阵D，才是分解一步所需要的计算量，因为有32个元素，因此计算花销为32。

因此，一个矩阵左乘 F 64 F_{64} F64​所用的乘法次数就从 6 4 2 64^2 642次变为了 2 ∗ ( 32 ) 2 + 32 2*(32)^2+32 2∗(32)2+32次。

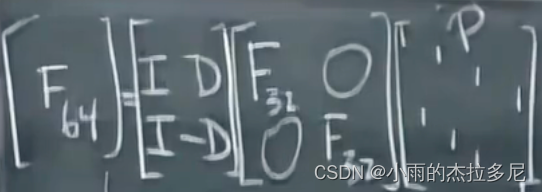
而得到的 F 32 F_{32} F32​又可以分解为 F 16 F_{16} F16​的组合。直到分解到1阶的傅立叶矩阵，因此复杂度从原先的 n 2 n^2 n2 变为了$1/2\ast n\ast logn$

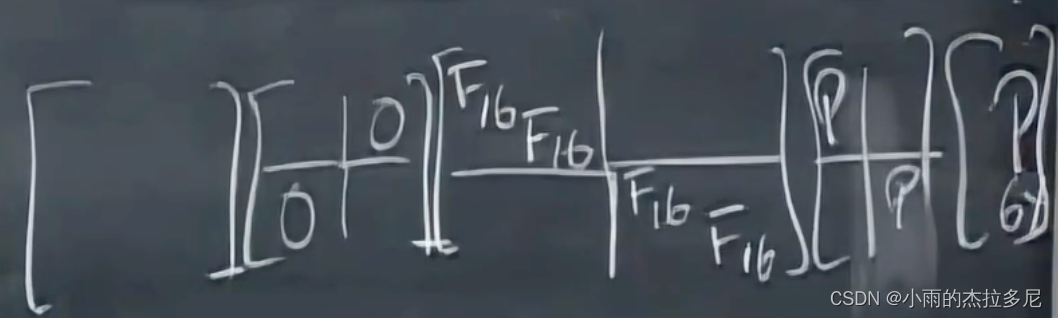
本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！