Sinusoids and Phasors

• 9.1 Introduction
• 9.2 Sinusoids(正弦量)
• • 中文部分
  • • 正弦量
    • 有效值(Effective value of sinusoids)
  • 英文部分
• 9.3 Phasors(相量)
• • 中文部分
  • • 复数概念
    • • 复数及其运算
      • 复数的四种表示形式
      • 复数运算
      • 旋转因子
    • 正弦量的相量表示法
    • 相量法基础
  • 英文部分
  • • Complex number
    • Phasor(相量法)
    • Phasor diagram(相量图)
• 9.4 Phasor Relationships for Circuit Elements(电路定律的相量形式)
• • 中文部分
  • 英文部分
• 9.5 Impedance and Admittance(阻抗和导纳)
• • 中文部分
  • • 阻抗(复阻抗)
    • 导纳(复导纳)
    • 阻抗和导纳的等效关系
    • 阻抗串联与并联
    • 电路的相量图
  • 英文部分
  • • Impedence
    • Admittance
• 9.6 Kirchhoff's Laws in the Frequency Domain
• 9.7 Impedance Combination
• • 例题
  • RLC parallel circuit

9.1 Introduction

dc circuits:Circuits excited by constant or time-invariant sources
Forcing function:

1. time-invariant sources(dc sources)
2. time-varying sources
3. sinusoidally time-varying excitation,or simply,excitation by a sinusoid

A sinusoid is a signal that has the form of the sine or or cosine function.
A sinusoidal current is usually referred to as alternating current (ac).
ac circuits:Circuits driven by sinusoidal current or voltage sources.

Interested in sinusoids for a number of reasons:
Nature itself is characteristically sinusoidal.
A sinusoidal signal is easy to generate and transmit.
Through Fourier analysis,any practical periodic signal(周期信号) can be represented by a sum of sinusoids.
A sinusoid is easy to handle mathematically.

The sinusoid is an extremely important function in circuit analysis.

9.2 Sinusoids(正弦量)

中文部分

正弦量

直流（DC或dc）：方向不随时间变化
交流（AC或ac）：方向随时间变化
正弦交流电:大小和方向随时间按正弦规律变化的电流或电压,简称正弦量
特点：周期性 交变性
正弦量的应用十分广泛,如：电能的产生和传输 电子技术中的信号
在指定参考方向下，表示为：
i = I m c o s ( w t + θ i ) u = U m c o s ( w t + θ u ) i=I_mcos(wt+θ_i)\\ u=U_mcos(wt+θ_u) i=Im​cos(wt+θi​)u=Um​cos(wt+θu​)

为避免混乱,统一采用cos

1. 正弦量的三要素(最大值,频率,初相位)
   以正弦电流为例
   瞬时值:正弦量在某一瞬时的量值，用小写字母表示
   (1) 最大值（幅值，振幅）
   正弦量在变化过程中出现的最大瞬时值，用大写字母加下标m表示
   (2)角频率
   表示正弦量变化的快慢
   
   我国大陆的工业标准频率是50Hz,美国加拿大也有采用60Hz的
   (3)初相位
   
   正弦量的三要素:实际上,正弦量的变化规律由幅值(最大值或振幅),频率(角频率或周期)和初相位确定
   
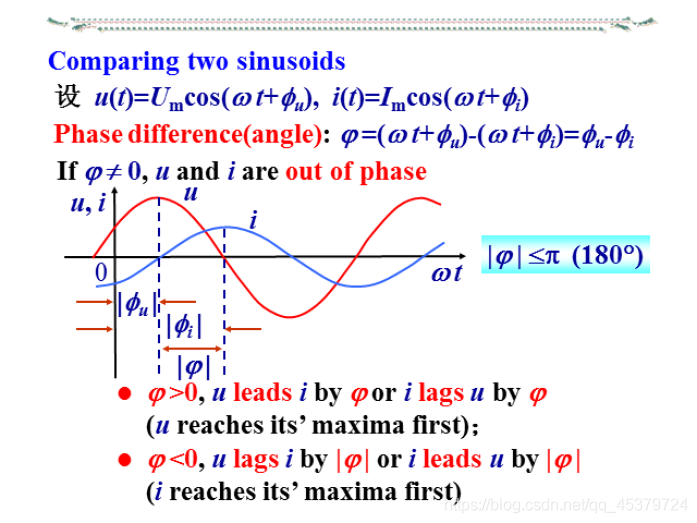
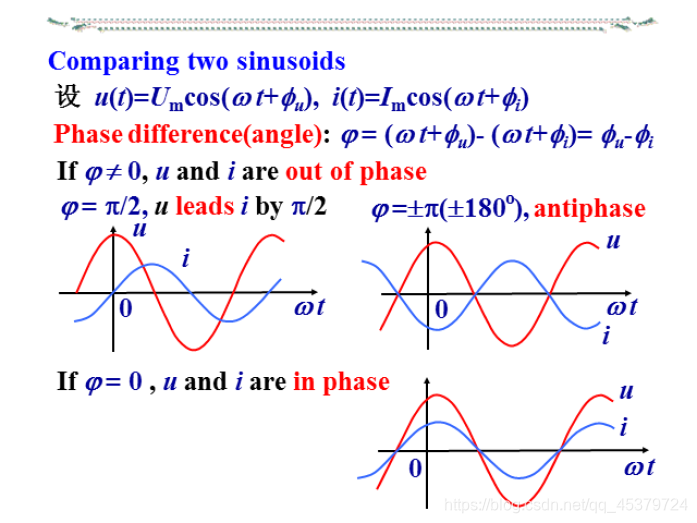
2. 相位差(同频率)
   任何两个同频率的正弦量的相位之差
   
   
   
   
   注意：
   （1）只有同频率的正弦量才比较相位差,它是不随时间改变的，不同频率的正弦量相位差无意义
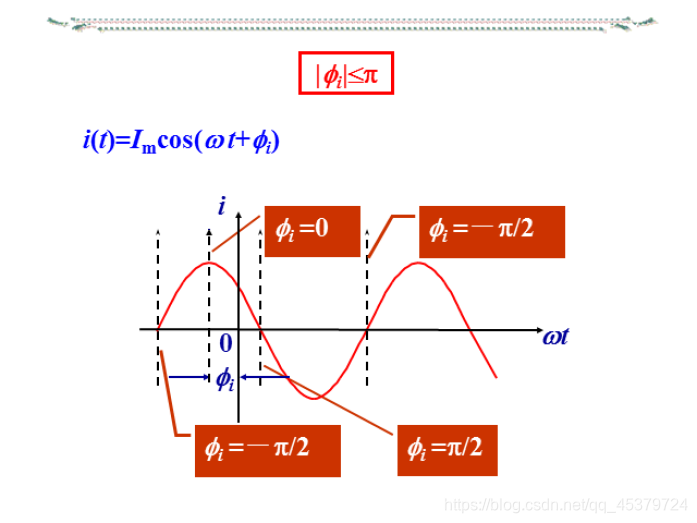
   （2）超前与滞后是相对的，如正弦电压超前电流也可说成电压滞后电流2π-φ。为避免混乱，相位差的取值一般限定在主值范围-π≤φ≤π之间

有效值(Effective value of sinusoids)

i = I m c o s ( w t + θ i ) u = U m c o s ( w t + θ u ) i=I_mcos(wt+θ_i)\\ u=U_mcos(wt+θ_u) i=Im​cos(wt+θi​)u=Um​cos(wt+θu​)

正弦量的瞬时值随时间而变，测量和计算都不方便

工程中，常将周期电流或电压在一个周期内产生的平均效应换算为等效的直流量，来衡量和比较周期电流或电压的效应，这一等效的直流量就称为周期量的有效值

如：周期电流 通过电阻R,R在一个周期T内吸收的电能


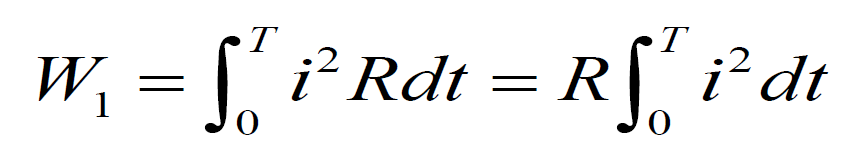
当直流电流 I 流过相同电阻R时,在相同的时间T内吸收的电能



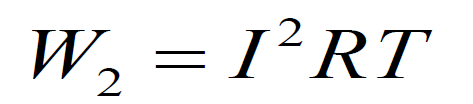
RMS=root-mean-square value
它是i的平方在一个周期内积分的平均值的平方根
等效的直流电流 I 称为周期电流 的有效值
有效值用相对应的大写字母表示

关于上面这个积分,余弦函数在一个周期内的积分为0

说明:
(1) 有效值的计算公式（方均根式）适用于任何周期性的变化量，但不能用于非周期量
(2) 工程中使用交流电气设备铭牌上标示出的额定电压、电流的数值，交流电压表、电流表显示的数字都是有效值
(3) 各种元电器的绝缘值或耐压值指的是最大值
(4) 正弦量的平均值为零
I a v = 1 T i ( t ) d t = 0 U a v = 1 T u ( t ) d t = 0 I_{av}=\frac{1}{T}i(t)dt=0\\ U_{av}=\frac{1}{T}u(t)dt=0 Iav​=T1​i(t)dt=0Uav​=T1​u(t)dt=0

英文部分

9.3 Phasors(相量)

中文部分

复数概念

复数及其运算

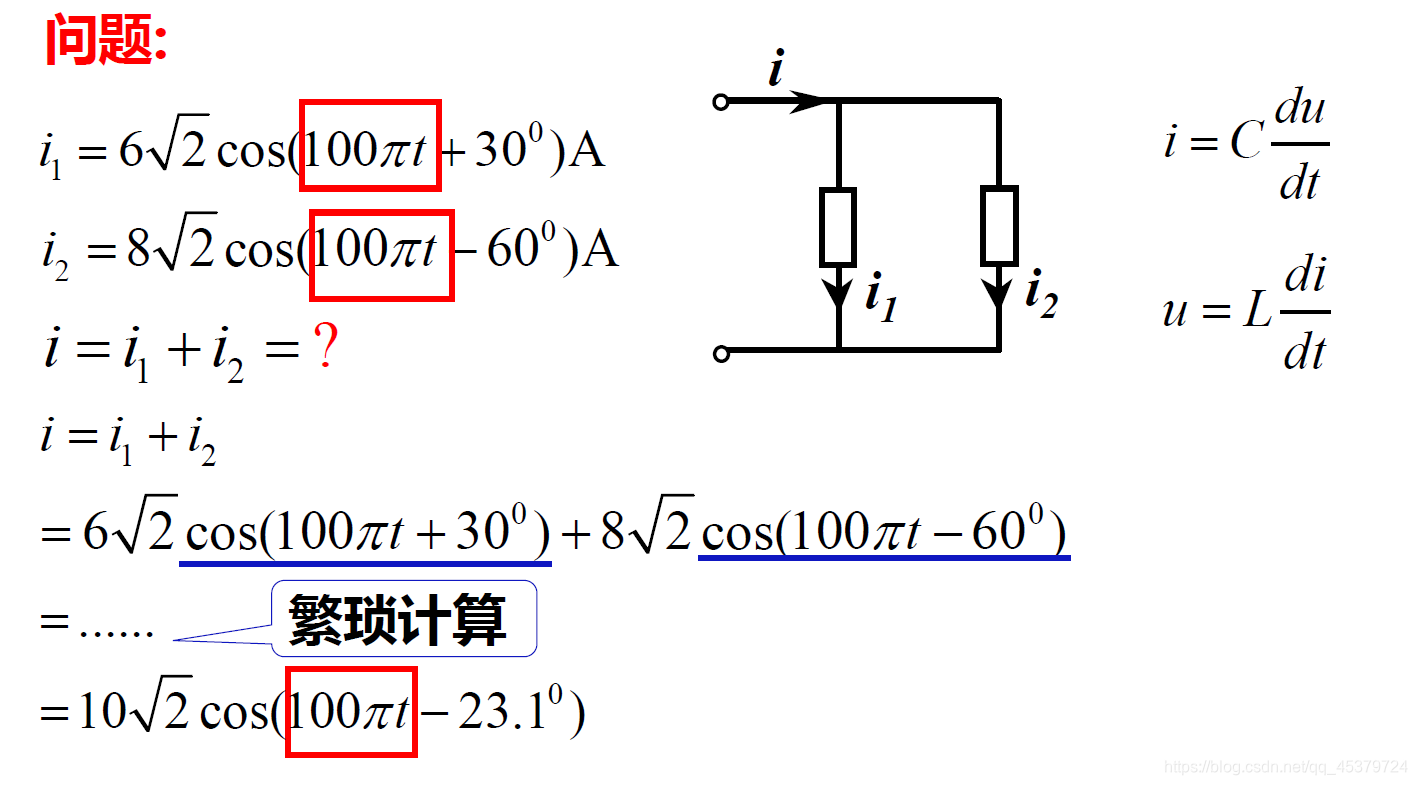
由于和差化积,微分积分造成的的繁琐运算

正弦量的重要性质
实际上，在线性非时变的正弦稳态电路中，只要电源的频率给定，电路响应（电流或电压）是同频率的正弦量
正弦量的三要素中，关键要确定有效值(或最大值)和初相位

由于电流符号为i,因此电路中的虚数单位统一用j,这也是积分变换中虚数单位为j的原因.

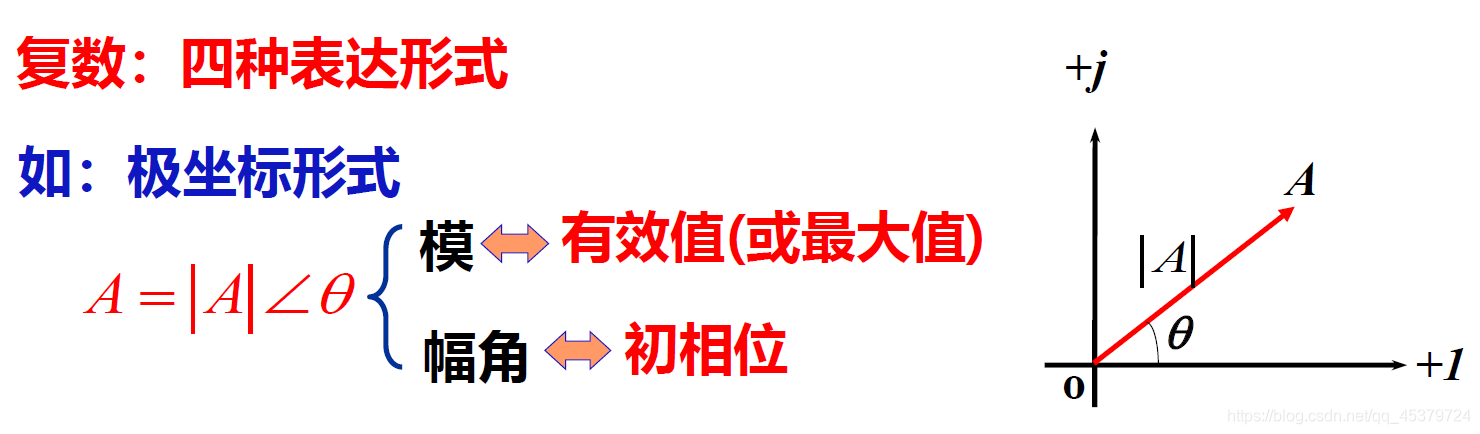
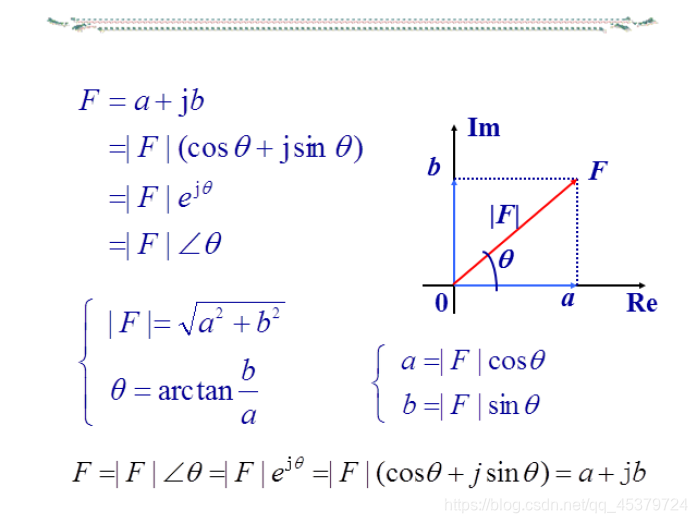
复数的四种表示形式

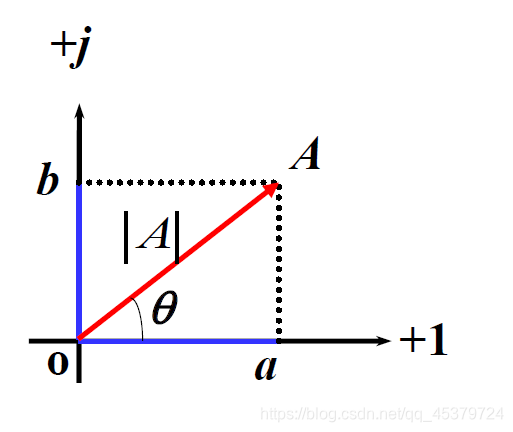
复数A可用复平面上的有向线段来表示
直角坐标形式 (代数形式）

极坐标形式

a=|A|cosθ b=|A|sinθ
三角函数形式

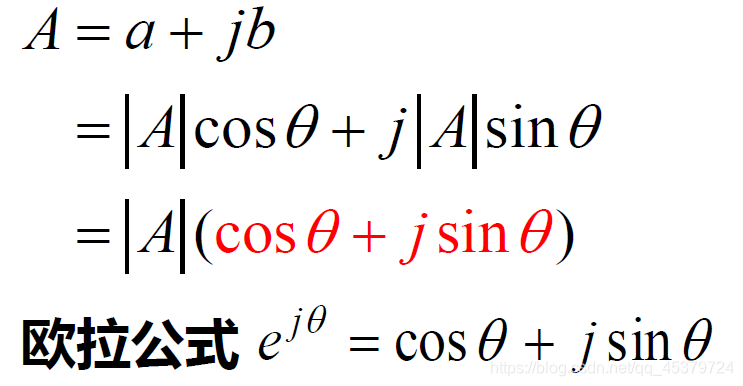
指数形式
A=|A|e^jθ

复数运算

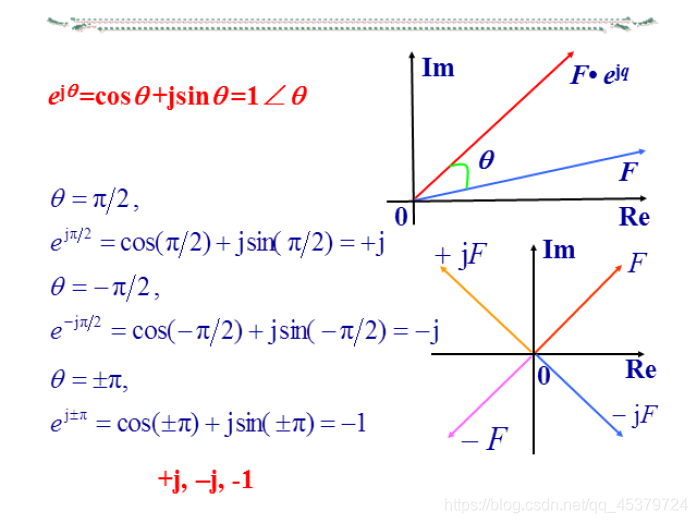
旋转因子

乘除运算作用大

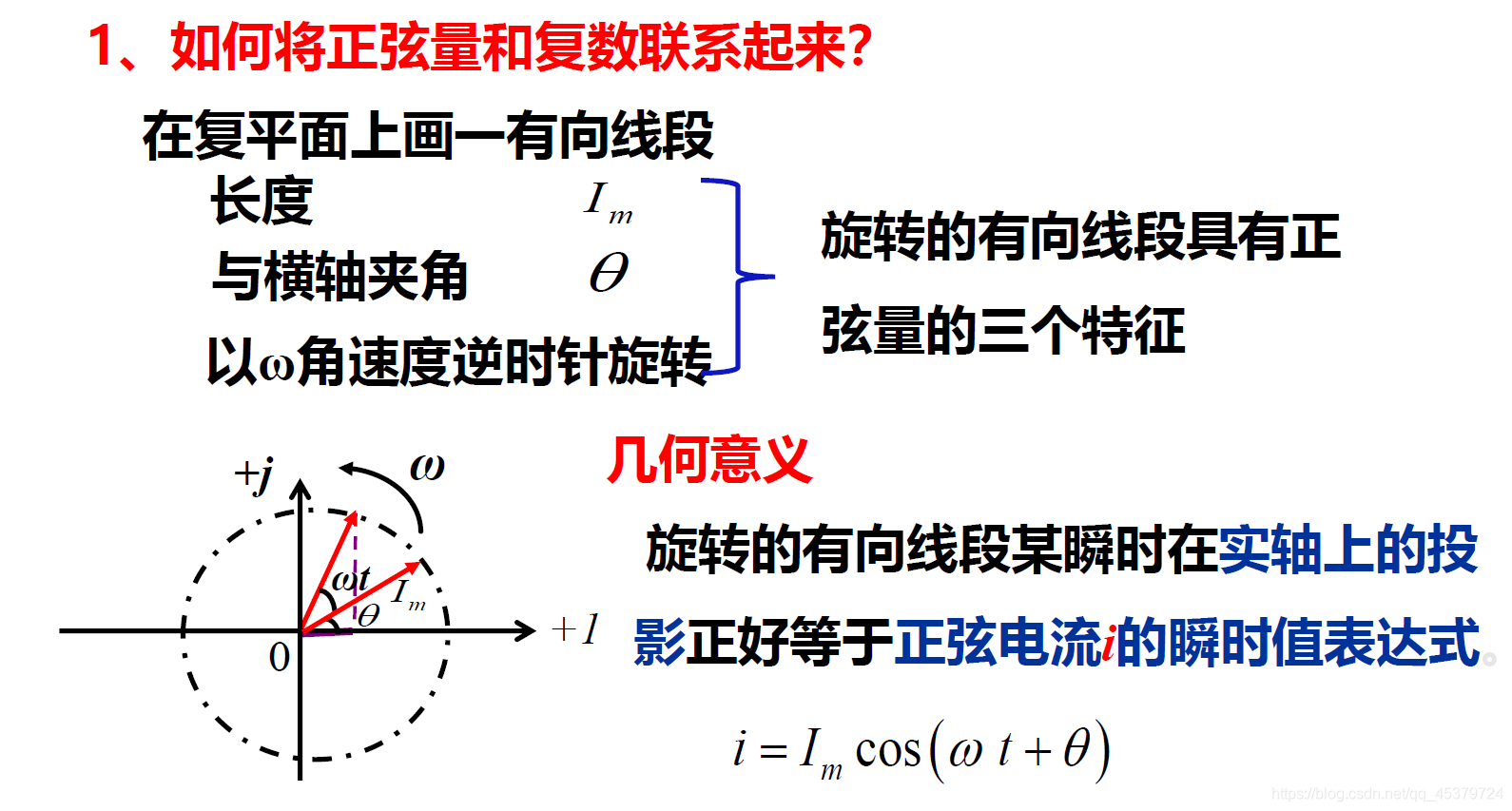
正弦量的相量表示法

1. 正弦量的重要性质
   在线性非时变的正弦稳态电路中，只要电源的频率给定，电路响应（电流或电压）是同频率的正弦量
   正弦量的三要素中，关键确定有效值(或最大值)和初相位
   
   
   
   
2. 正弦量的相量表示法
   为了和一般的复数相区别，我们把表示正弦量的复数称为相量，并在大写字母上加点来表示相量。
   
   
   说明：
   （1）正弦量和其相量之间是一一对应的关系.相量只是用来表示正弦量,但并不等于正弦量
   相量是复常数,其模是该正弦量的有效值(最大值),其辐角是该正弦量的初相位
   
   （2）相量的运算规则即复数的运算规则
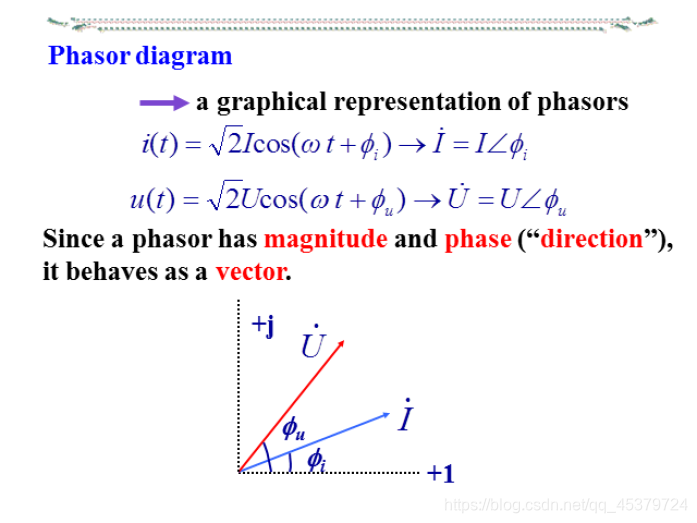
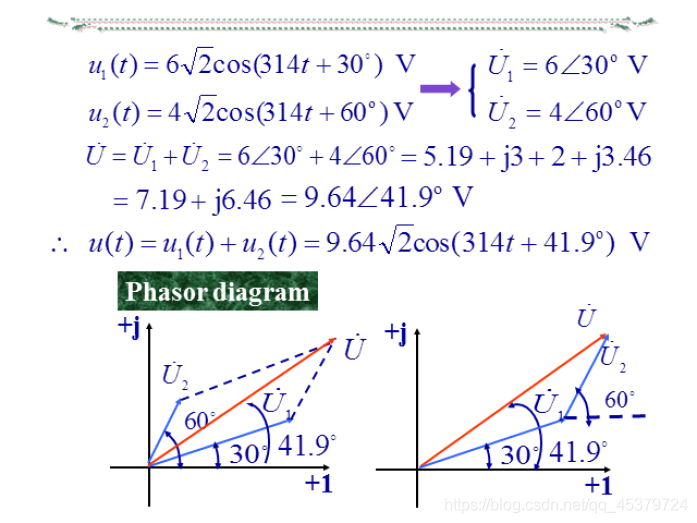
   相量也可用有向线段表示，将几个同频率的正弦量在同一个复平面上用相量表示出来，所得到的图形称为相量图
   在相量图中能清楚地看出各相量的相位关系
   
   一般写有效值表达式
   

相量法基础

将正弦稳态交流电路中的电压、电流用相量表示，用相量形式求解正弦交流电路——相量法
相量法：以复数运算代替正弦量运算
目的是简化运算

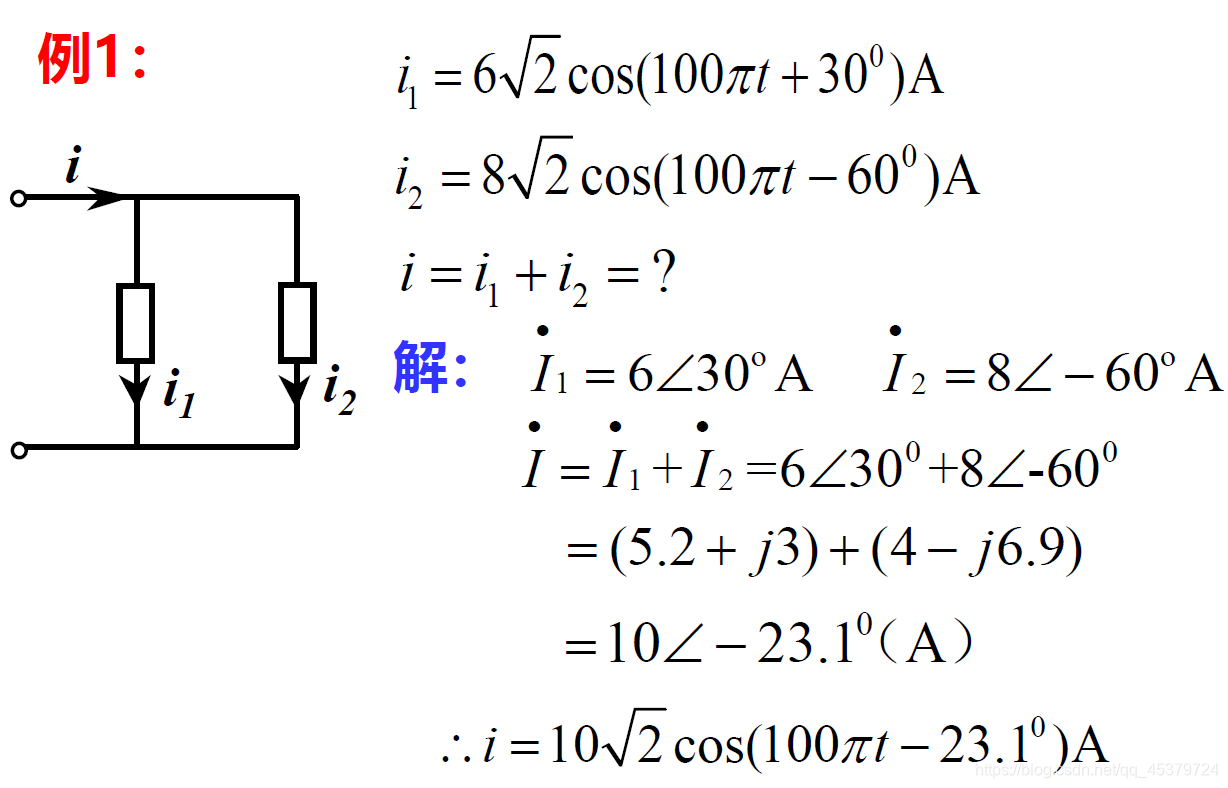
1. 同频率正弦量相加减
   
   
2. 正弦量的微分运算(乘以jw)
   正弦量的微分,对应相量等于原正弦量对应的相量乘以jw
   
3. 正弦量的积分运算(除以jw)
   
   
   

相量法的优点
(1) 将时域问题变为复数问题
(2) 把微积分方程的运算变为复数方程运算
(3) 可以把直流电路的分析方法直接用于交流电路

注意：相量法只适用于激励为同频正弦量的线性电路
线性电路是指完全由线性元件,独立源或线性受控源构成的电路
线性元件现阶段,就是电阻,电容,电感

英文部分

Complex number

Phasor(相量法)

幅值对应有效值

Phasor diagram(相量图)

a graphical representation of phasors
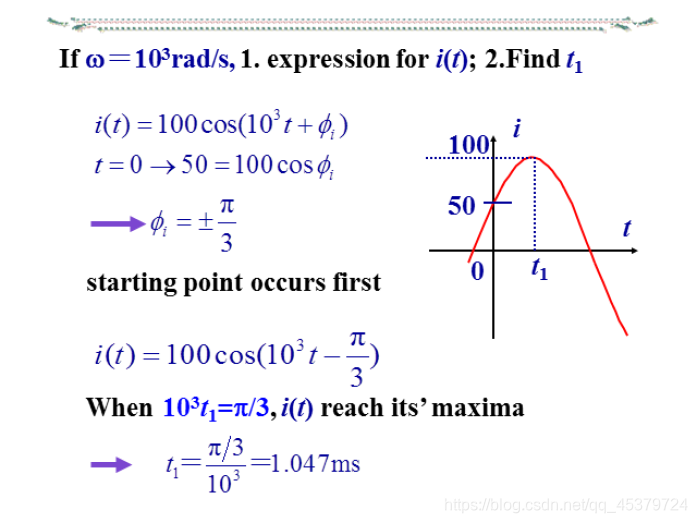
i ( t ) = 2 I c o s ( w t + ϕ i ) i(t)=\sqrt{2}Icos(wt+ϕ_i) i(t)=2 ​Icos(wt+ϕi​)

实数域里面微分就是乘jw,相当于旋转90°;积分是除以jw

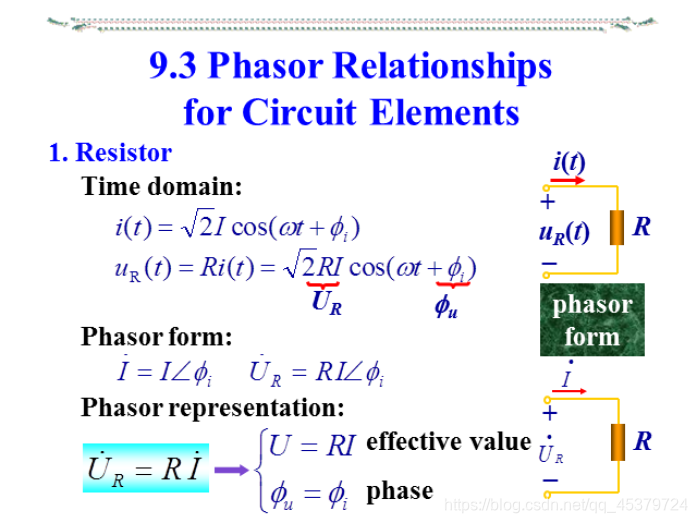
9.4 Phasor Relationships for Circuit Elements(电路定律的相量形式)

中文部分

1. 基尔霍夫定律的相量形式(同频代数和为0)
   同频正弦量的加减运算可变成对应相量的加减运算
   在正弦交流电路中，KCL和KVL可用相应的相量形式表示
   
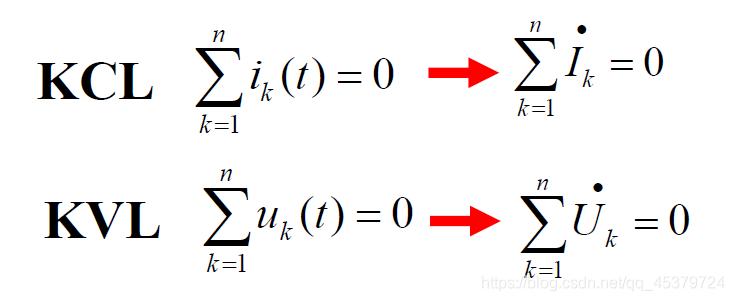
   任一结点同频正弦电流对应相量的代数和等于零
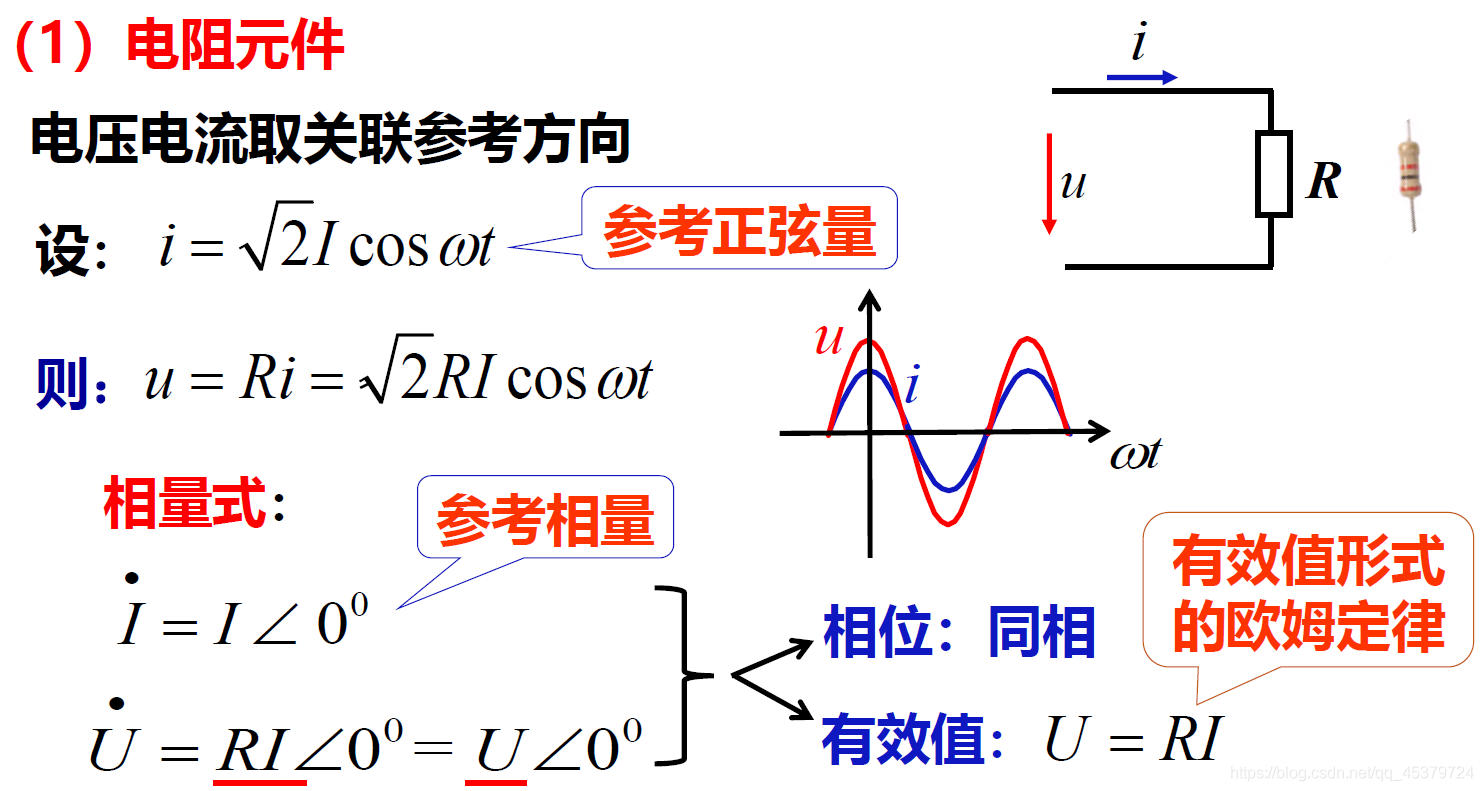
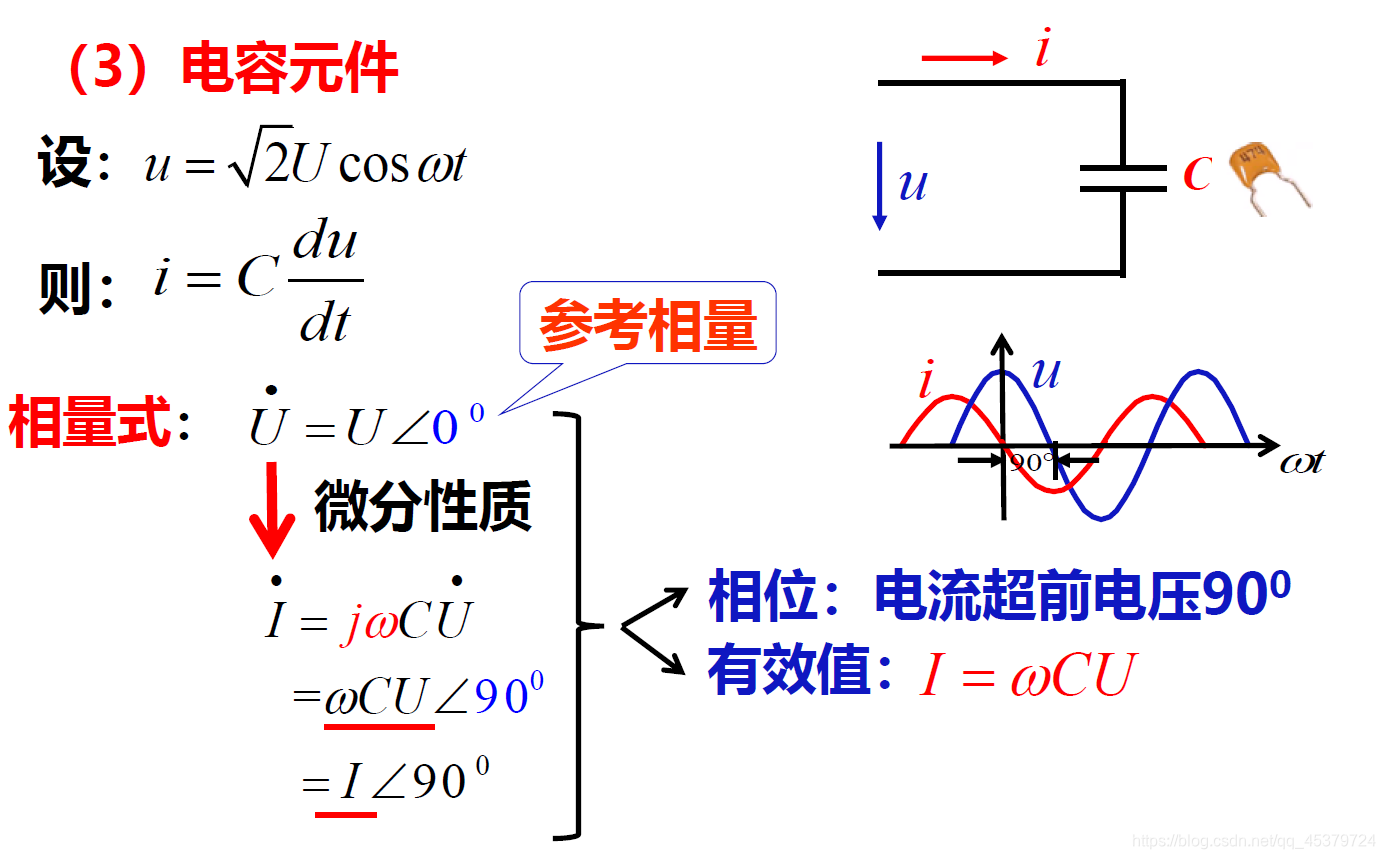
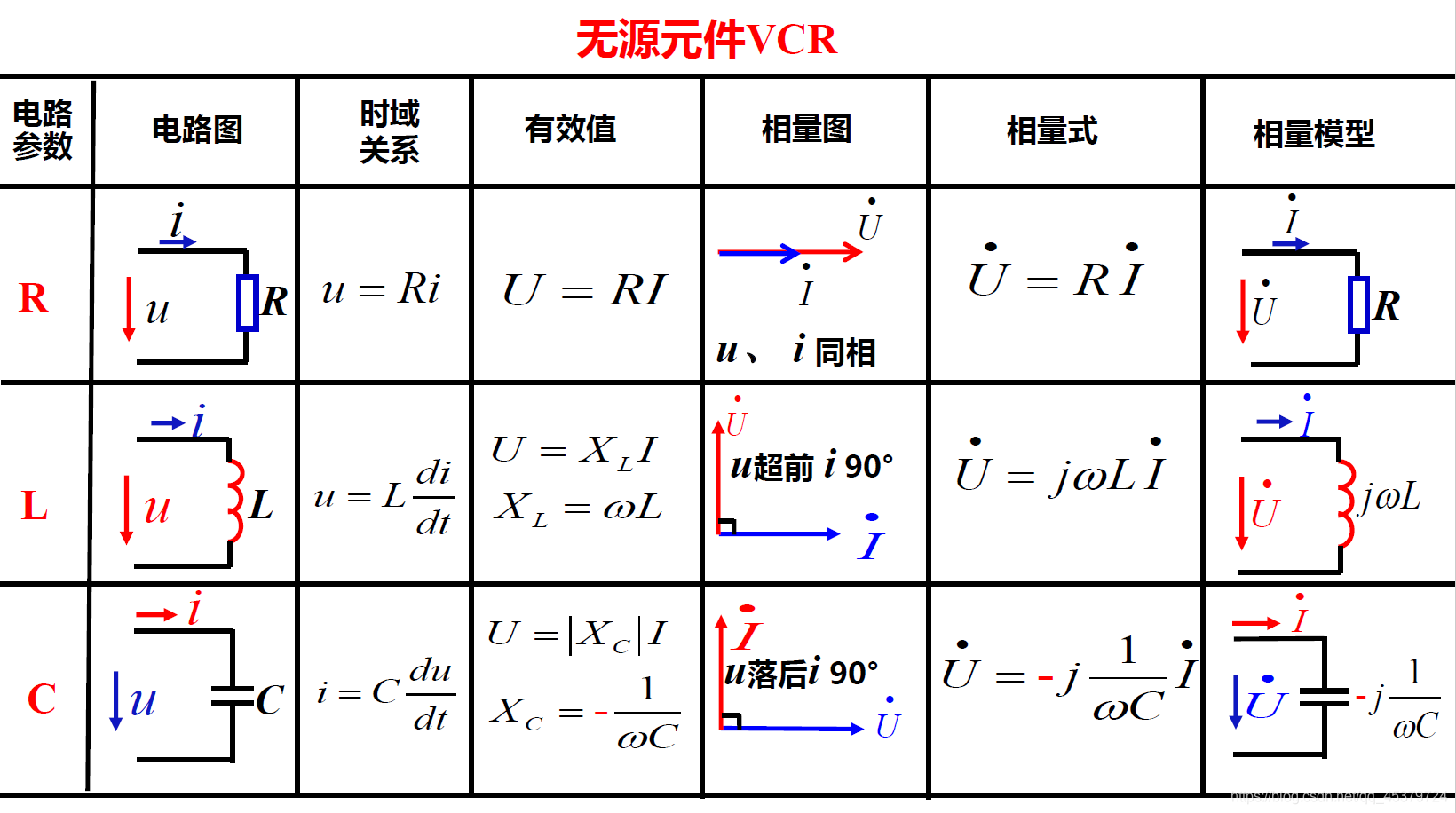
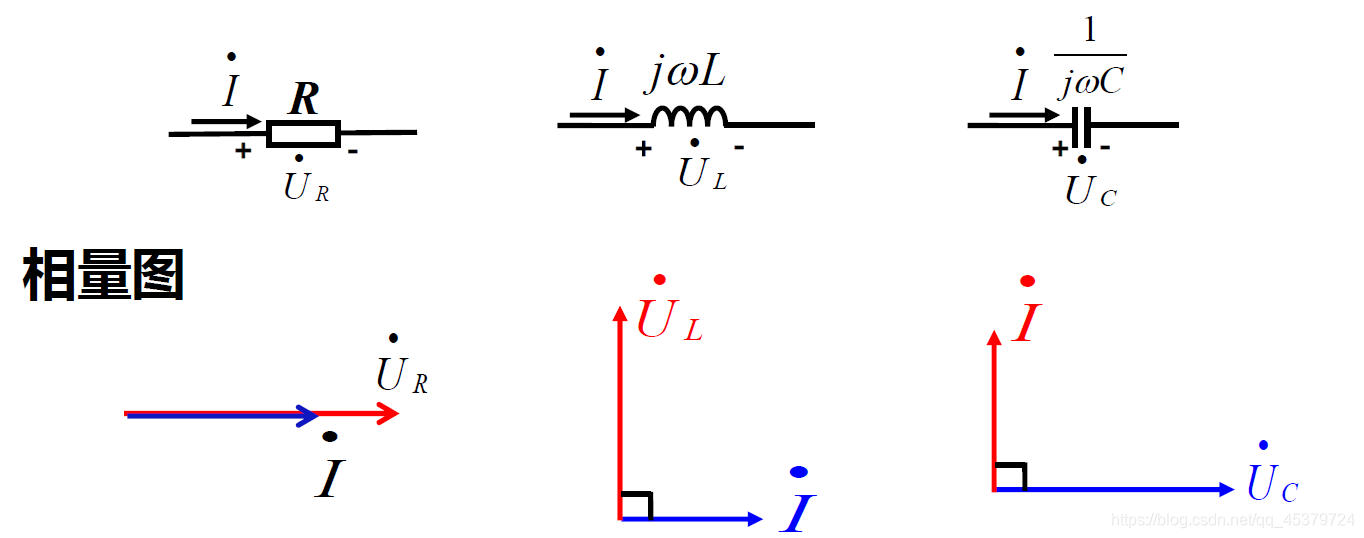
   任一回路同频正弦电压对应相量的代数和等于零
2. 无源元件VCR的相量形式(电阻 电容 电感)
   1)电阻(电压电流同相)
   
   
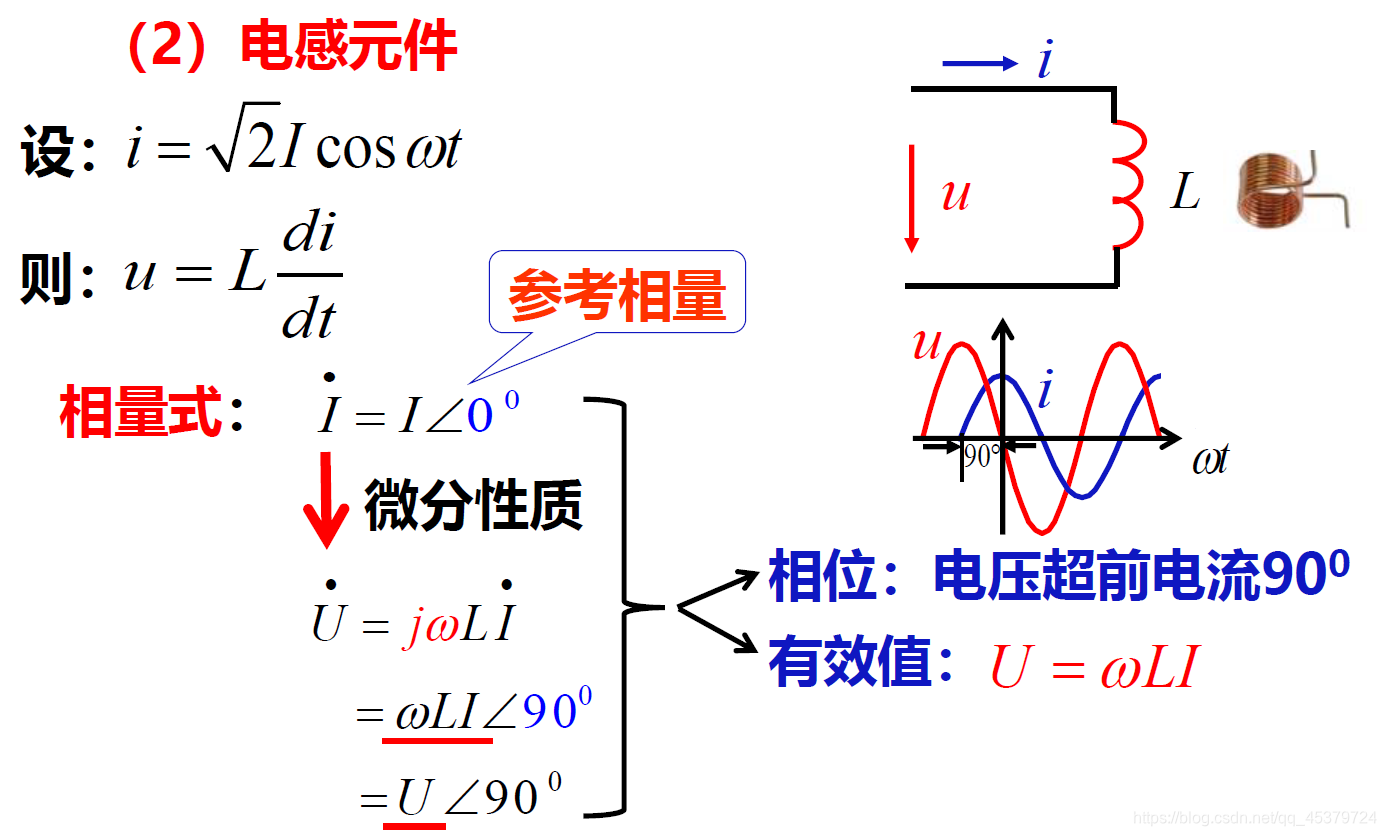
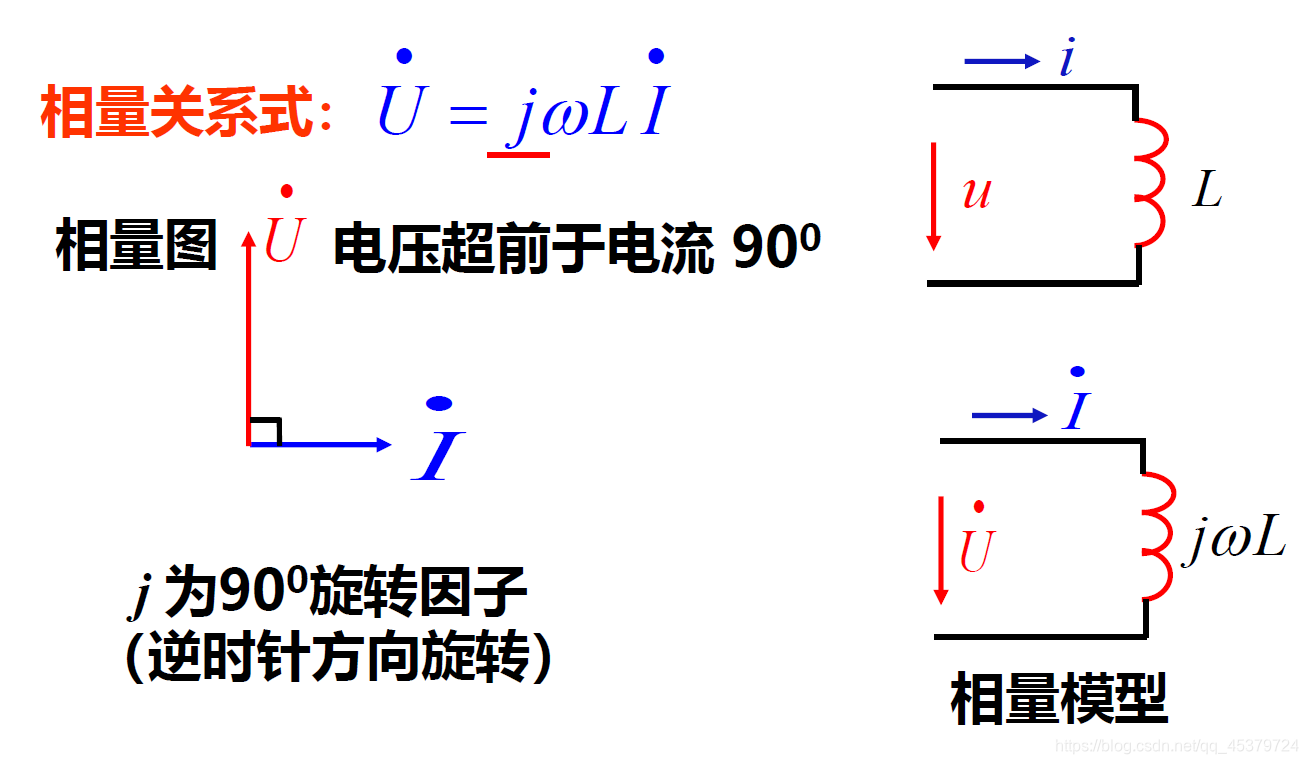
   2)电感(jωL,电压超前电流90°)
   
   
   
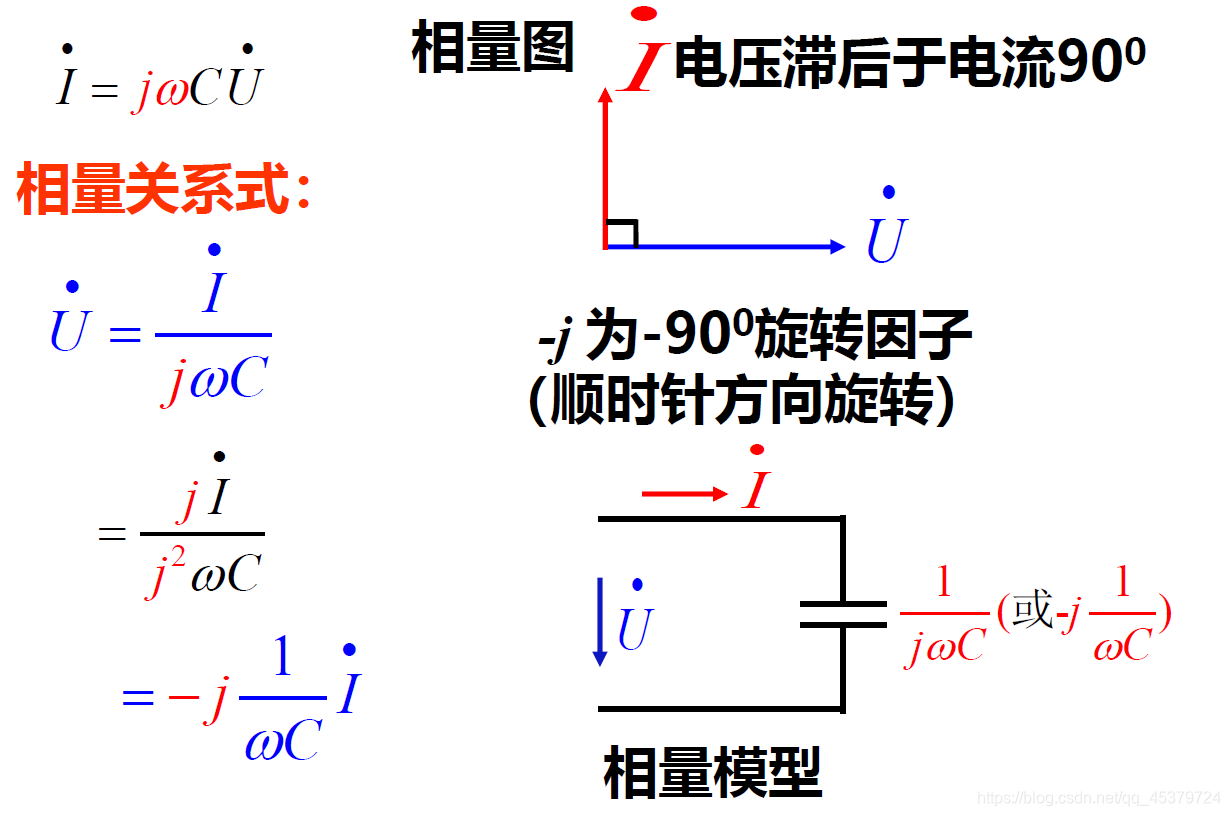
   3)电容( 1 j ω C \frac{1}{jωC} jωC1​,电流超前电压90°)
   
   
   
   
   总结
   

英文部分

不能把j丢掉L→jwL



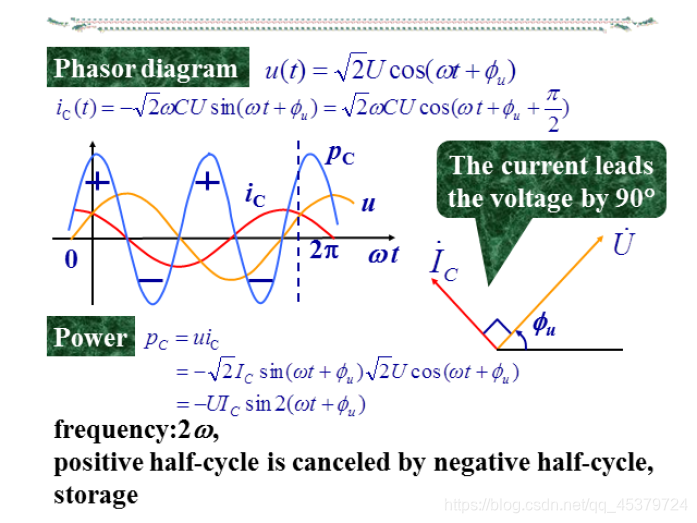
电感电流滞后电压90°
U ˙ = U ∠ ϕ u \dot{U}=U∠ϕ_u U˙=U∠ϕu​

9.5 Impedance and Admittance(阻抗和导纳)

中文部分

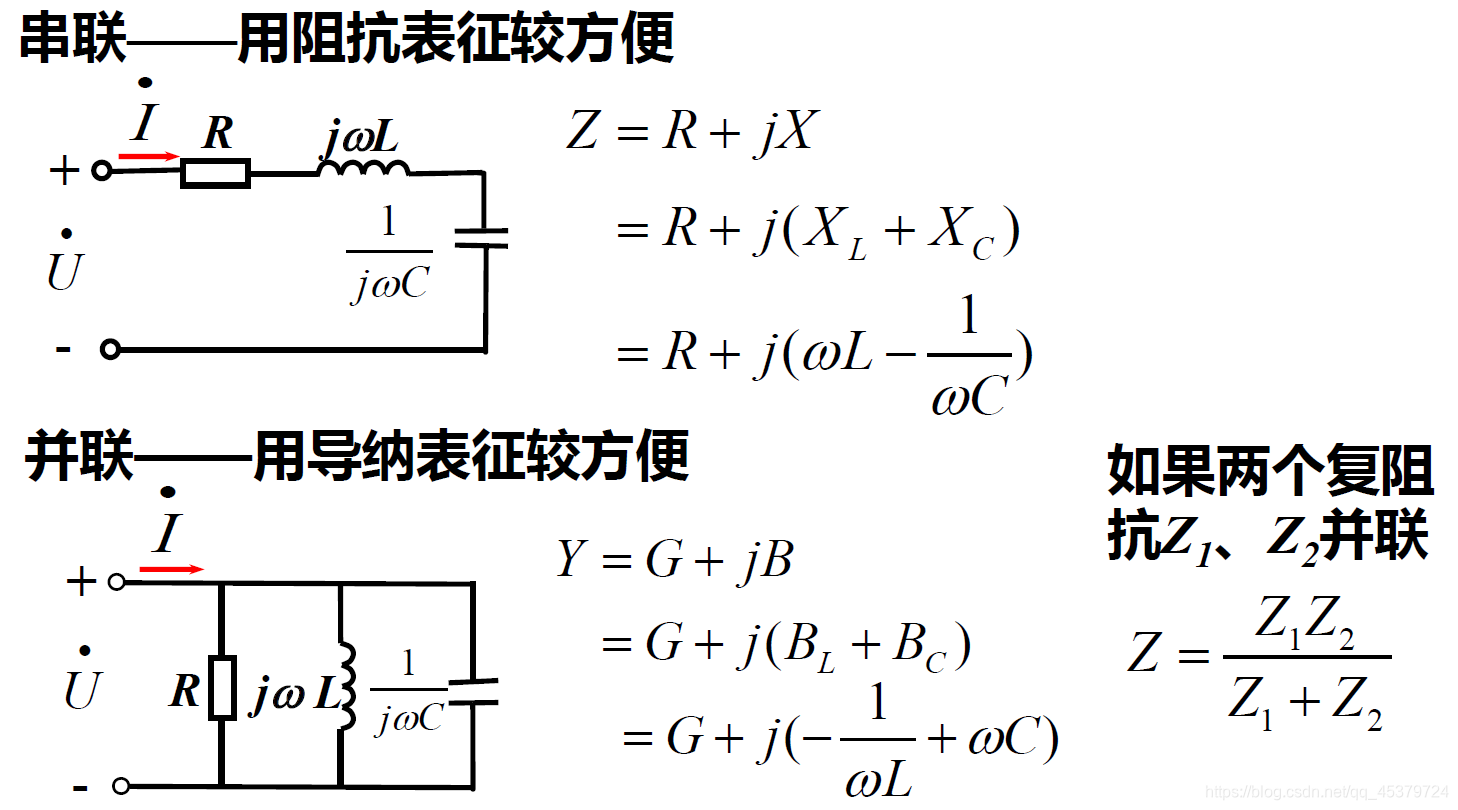
阻抗(复阻抗)

Z是复数,但不是正弦量,所以上面不打点

导纳(复导纳)

三种基本元件的阻抗和导纳

阻抗和导纳的等效关系

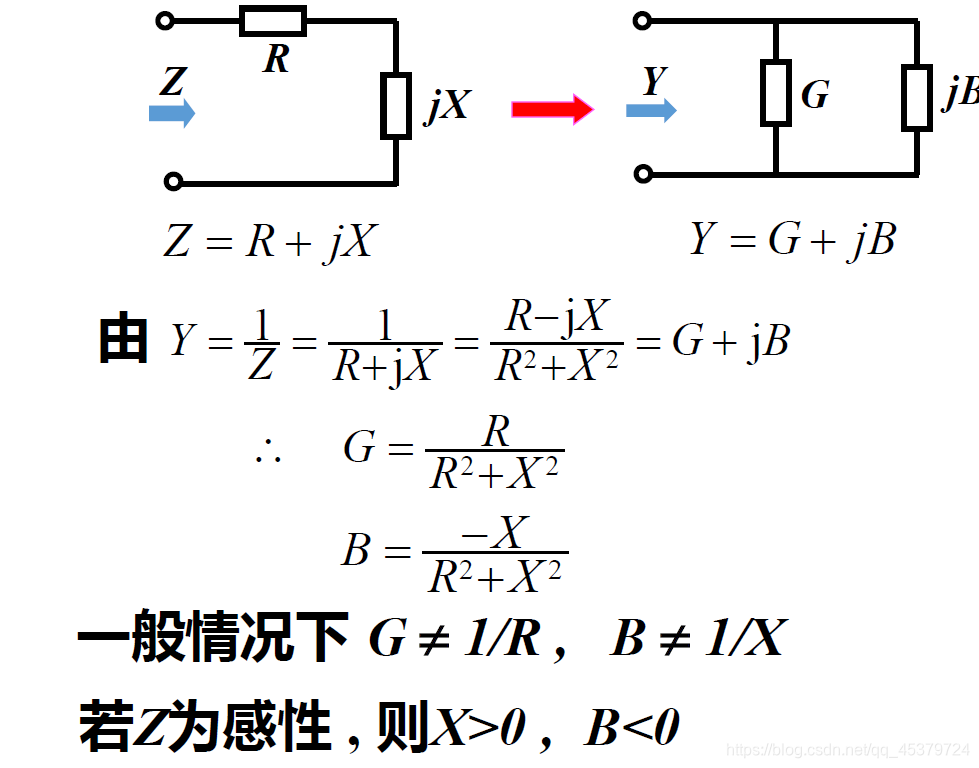
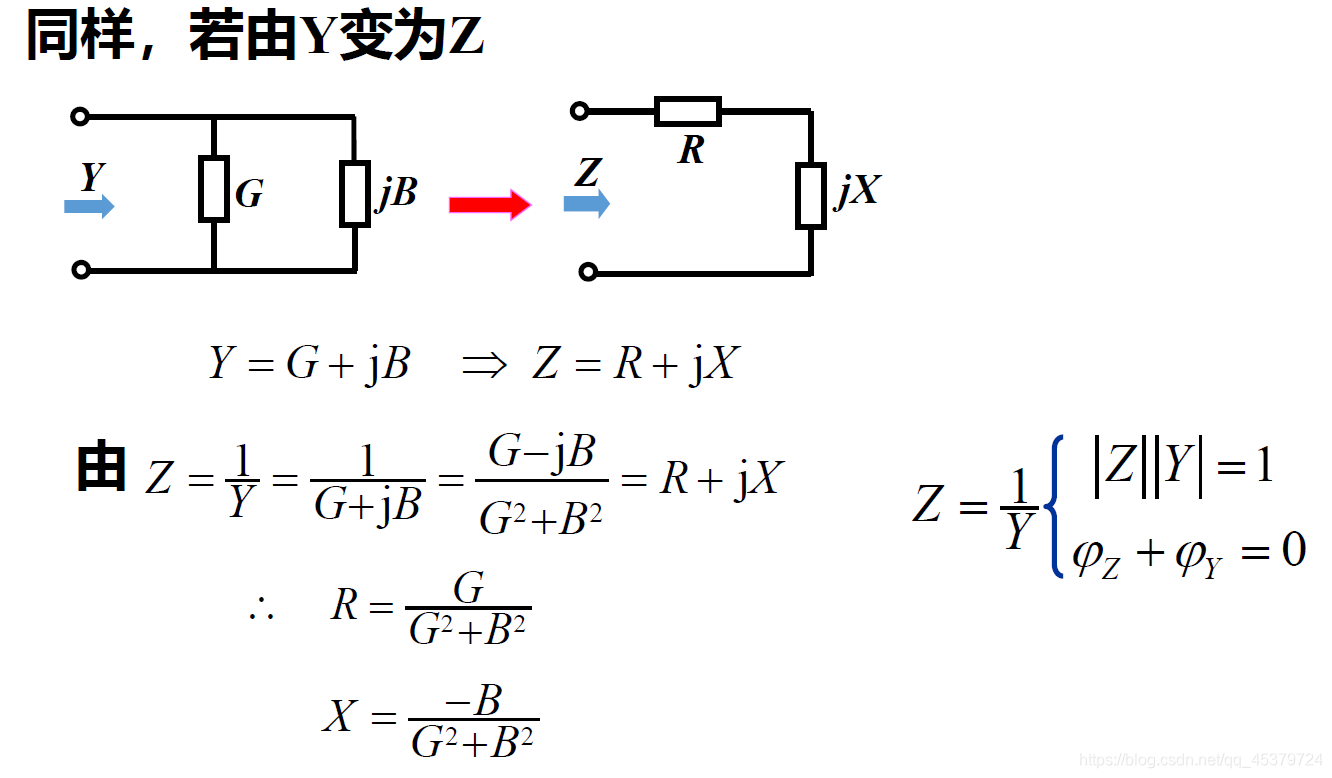
阻抗串联与并联

1. n个阻抗串联
   
2. n个导纳并联
   
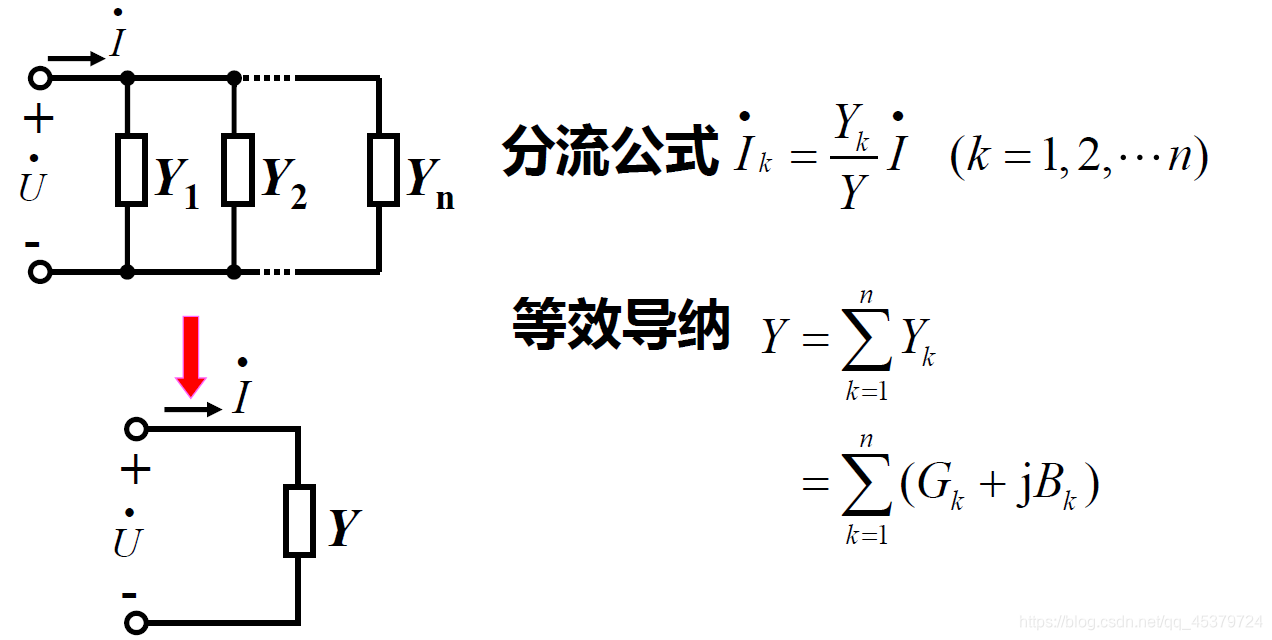
   运算时阻抗和导纳的选择
   
   

电路的相量图

正弦量可用相量表示，相量可用有向线段表示
将几个同频率的正弦量在同一个复平面上用相量表示出来（只画出t=0时的初始位置，长度一般用有效值表示）
所得到的图形称为相量图

（1）相量图能直观显示各相量的大小和相位关系
（2）可辅助电路的分析计算

1. 相量图绘制依据
   
   
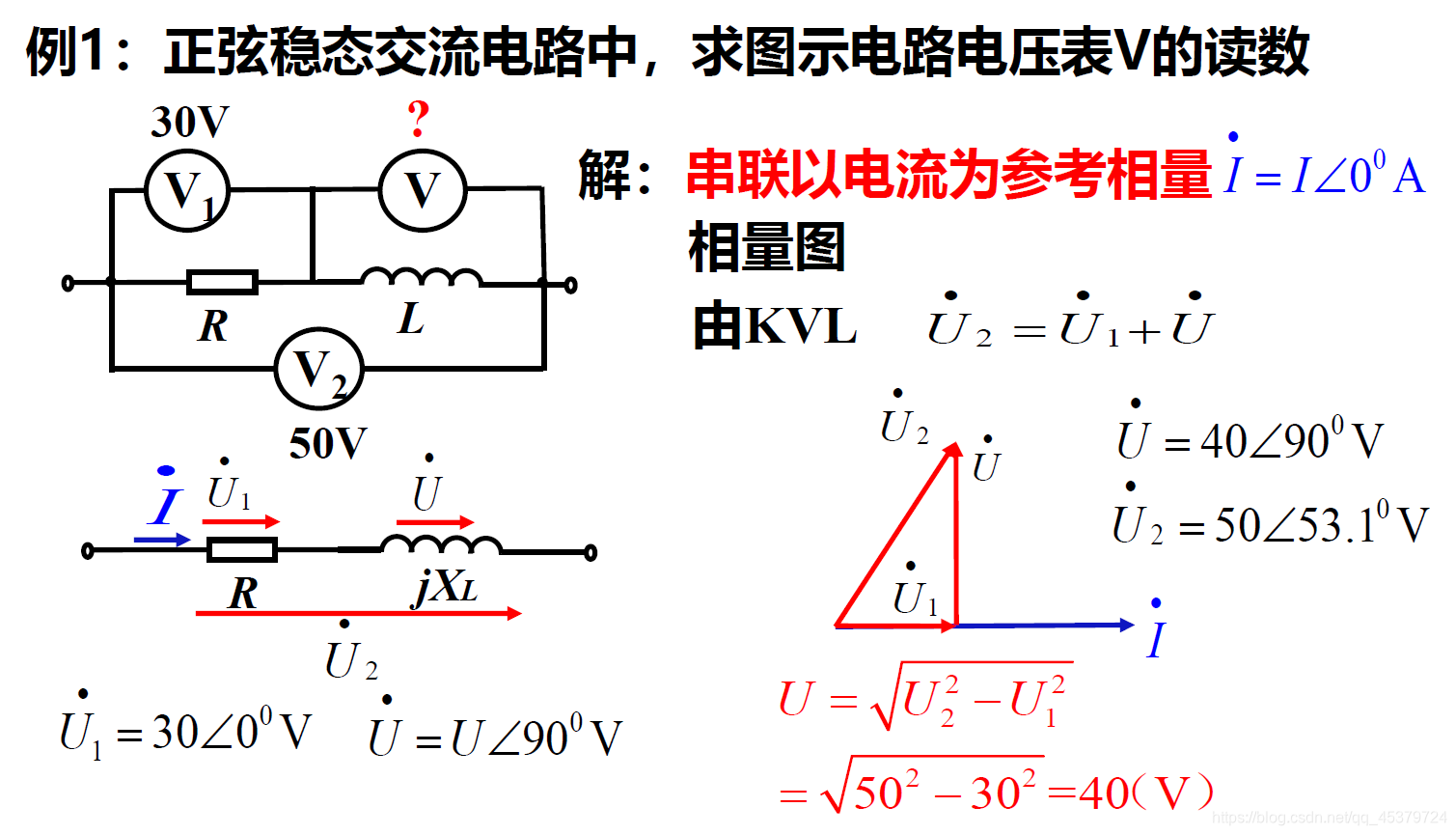
2. 相量图绘制的方法
   （1）选择参考相量
   通常参考相量的初相取为零（或视具体情况取值）
   串联电路：取电流为参考相量
   并联电路：取电压为参考相量
   串并联电路：从局部开始，视情况定
   （2） 根据支路VCR画出支路电压或电流的相量
   （3） 由KCL或KVL画出封闭图形
   
   
   
   相量图绘制小结：
   (1)相量的初相是指与实轴的夹角，由它确定相量在复平面上的位置
   画相量图时实轴虚轴可省略不画关键是确定各相量的相位关系
   (2)按比例画出各相量的模
   回路电压或结点电流相量构成封闭的图形
   有时候可根据电路的参数和结构定性地画出相量图，以辅助电路的求解

英文部分

Impedence

The impedence of a circuit is the ratio of the phasor voltage to the phasor current,measured in ohms.
Z = d e f U ˙ I ˙ = ∣ Z ∣ ∠ φ z Ω Z\overset{def}{=} \frac{\dot U}{\dot I}=|Z|∠φ_zΩ Z=defI˙U˙​=∣Z∣∠φz​Ω
{ ∣ Z ∣ = U I Ω φ z = θ u − θ i \begin{cases} |Z|=\frac{U}{I}Ω\\ φ_z=θ_u-θ_i \end{cases} {∣Z∣=IU​Ωφz​=θu​−θi​​
阻抗是复数,不对应正弦量,因为其不随时间变化

Admittance

Although the imdedance(admittance) is the ratio of two phasors,it is not a phasor,because it does not correspond to a sinusoidally varying quantity.

KCL/KVL,节点电压,回路电流,最大功率定理一两个(戴维南),三要素法一两个题,开卷考试

9.6 Kirchhoff’s Laws in the Frequency Domain

In sinusoidal steady state:
∑ i ( t ) = 0 → ∑ i ( t ) = ∑ R e 2 [ I 1 ˙ + I 2 ˙ + ⋯ ] e j w t = 0 → ∑ I ˙ = 0 ∑ u ( t ) = 0 → ∑ U ˙ = 0 ∑i(t)=0\\ →∑i(t)=∑Re\sqrt2[\dot{I_1}+\dot{I_2}+\cdots] e^{jwt}=0\\ →∑\dot{I}=0\\ ∑u(t)=0\\ →∑\dot{U}=0 ∑i(t)=0→∑i(t)=∑Re2 ​[I1​˙​+I2​˙​+⋯]ejwt=0→∑I˙=0∑u(t)=0→∑U˙=0
Kirchhoff’s current law holds for phasors
Kirchhoff’s voltage law holds for phasors
U ˙ A C \dot{U}_{AC} U˙AC​


电流超前电压

U ˙ L = j w L I ˙ L U ˙ C = 1 j w C I ˙ = − 1 w C I ˙ U ˙ R = R I ˙ \dot{U}_L=jwL\dot{I}_L\\ \dot{U}_C=\frac{1}{jwC}\dot{I}=-\frac{1}{wC}\dot{I}\\ \dot{U}_R=R\dot{I} U˙L​=jwLI˙L​U˙C​=jwC1​I˙=−wC1​I˙U˙R​=RI˙



注意:in phase,同相,相当于谐振,等效电阻为一个纯电阻容抗为负值

9.7 Impedance Combination

Impedances in series and parallel
①Impedances in series
阻抗分压

②Impedances in parallel
导纳分流


RLC series circuit


KVL:


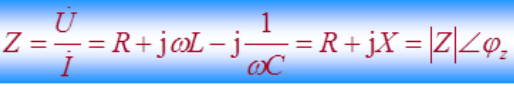
Z − I m p e d a n c e ∣ Z ∣ − M a g n i t u d e o f Z φ Z − P h a s e o f Z R − R e s i s t a n c e ( = R e Z ) X − R e a c t a n c e ( = I m Z ) R e l a t i o n s h i p : Z-Impedance\\ |Z|-Magnitude of Z\\ φ_Z-Phase of Z\\ R-Resistance(=Re Z)\\ X-Reactance(=Im Z)\\ Relationship: Z−Impedance∣Z∣−MagnitudeofZφZ​−PhaseofZR−Resistance(=ReZ)X−Reactance(=ImZ)Relationship:

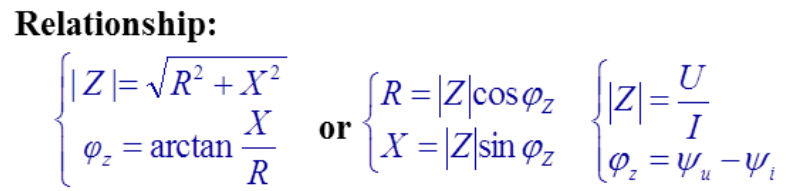
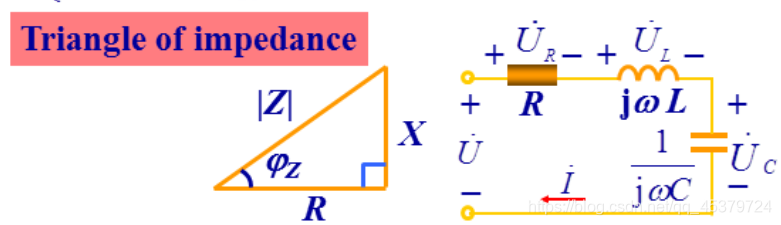
感抗和容抗相同,等效纯电阻电路

激励的频率发生变化会导致电路性质改变

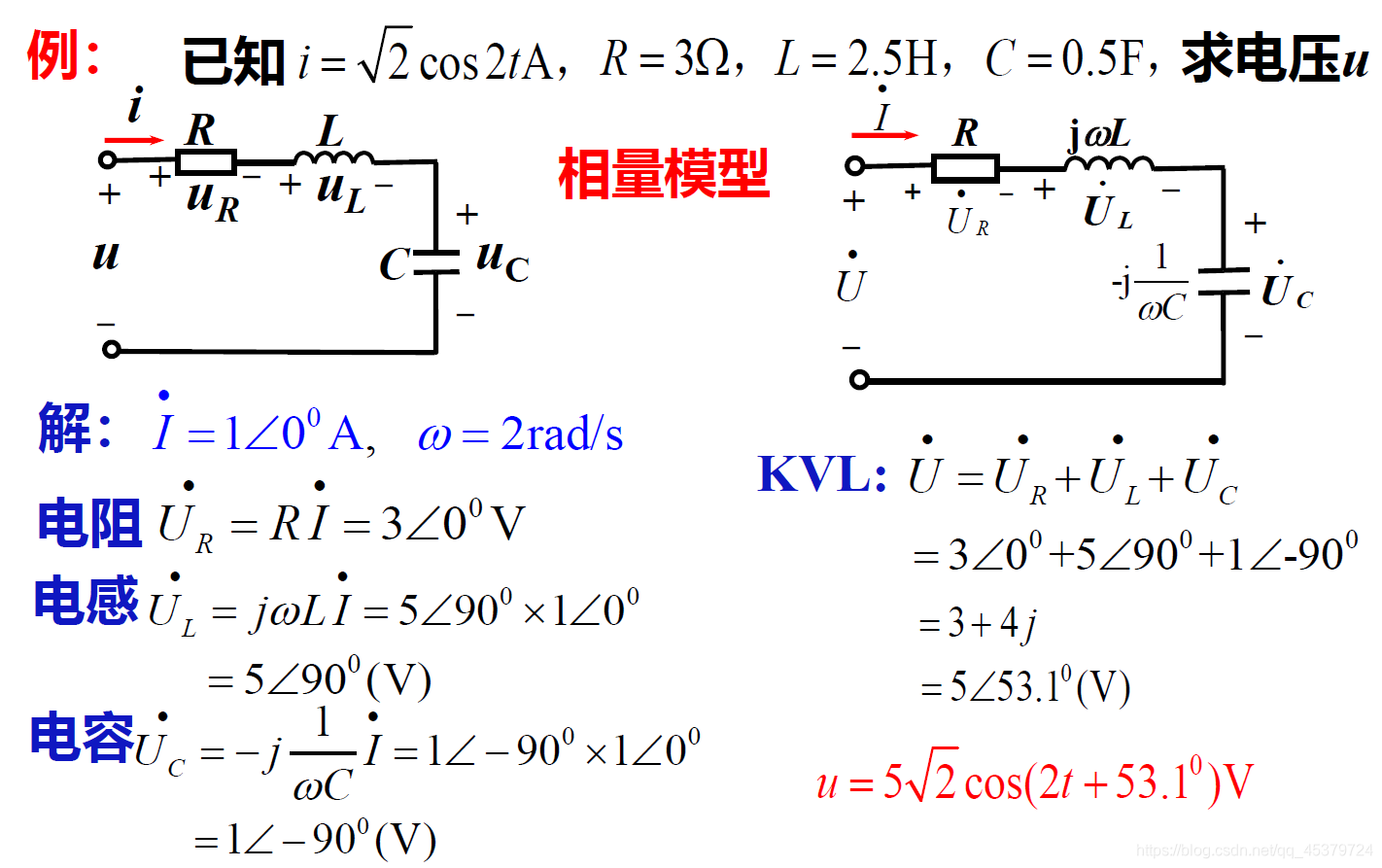
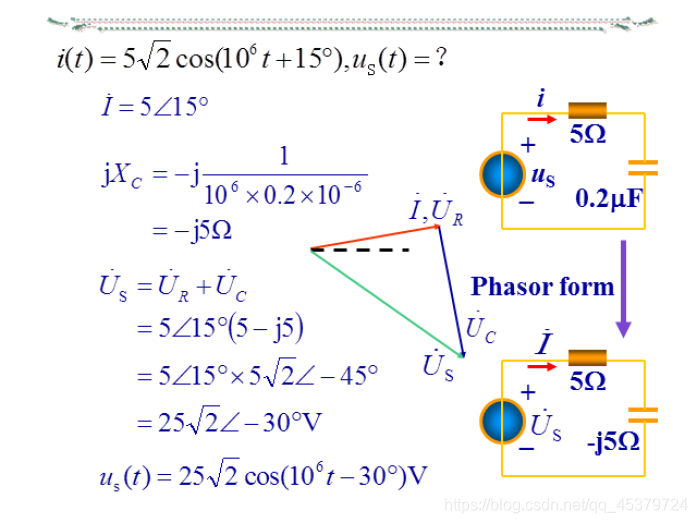
例题

交流电压,电感电压有效值>总电压,电感电压超前电流,电容电压滞后电流,电感电压最大时,电容电压最小

RLC parallel circuit

实部电导,虚部电纳





等效之后,电路性质不会发生变化



阻抗(导纳)是复数,但不是向量
阻抗(导纳)与频率有关


移相器

ωRC=1,只要修改对应RC,即可获得需要的ω值

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！