马尔可夫系列概念
| 不考虑动作 | 考虑动作 | |
| 状态完全可见 | 马尔可夫链(MC) | 马尔可夫决策过程(MDP) |
| 状态不完全可见 | 隐马尔可夫模型(HMM) | 部分可观察马尔可夫决策(POMDP) |
一、马尔可夫性质(Markov property)
1、定义
当一个随机过程在给定现在状态及所有过去状态情况下,其未来状态的条件概率分布仅依赖于当前状态;换句话说,在给定现在状态时,它与过去状态(即该过程的历史路径)是条件独立的,那么这个随机过程即具有马尔可夫性质。具有马尔可夫性质的过程通常称之为马尔可夫过程。
简单地说,就是系统的下个状态只与当前状态信息有关,与更早之前的状态无关,即“无记忆性”。
2、数学描述
如果X(t),t>0为一个随机过程,则马尔可夫性质就是指 P r [ X ( t + h ) ] = y ∣ X ( s ) = x ( s ) , s ≤ t ] = P r [ X ( t + h ) = y ∣ X ( t ) = x ( t ) ] , ∀ h > 0. Pr[X(t+h)]=y|X(s)=x(s),s \le t] = Pr[X(t+h)=y|X(t)=x(t)], \forall h>0. Pr[X(t+h)]=y∣X(s)=x(s),s≤t]=Pr[X(t+h)=y∣X(t)=x(t)],∀h>0.
二、马尔可夫链(MC)
1、定义
数学中具有马尔可夫性质的离散时间随机过程。状态空间中经过一个状态到另一个状态的转换的随机过程。这个过程要求具备马尔可夫性质。实际上这样干脆的过程可能是很少的,但很多时候在满足要求的前提下使用马尔可夫链的可以大大简化模型的复杂度。
2、数学定义
假设状态序列为 . . . , x t − 2 , x t − 1 , x t , x t + 1 , x t + 2 , . . . ...,x_{t-2},x_{t-1},x_{t},x_{t+1},x_{t+2},... ...,xt−2,xt−1,xt,xt+1,xt+2,...,由马尔可夫链定义可知,时刻 x t + 1 x_{t+1} xt+1的状态只与状态 x t x_{t} xt有关,用数学公式来描述: P ( x t + 1 ∣ . . . , x t − 2 , x t − 1 , x t ) = P ( x t + 1 ∣ x t ) P(x_{t+1}|...,x_{t-2},x_{t-1},x_{t}) = P(x_{t+1}|x_{t}) P(xt+1∣...,xt−2,xt−1,xt)=P(xt+1∣xt)既然某一时刻状态转移的概率只依赖前一个状态,那么只要求出系统中任意两个状态之间的转移概率,这个马尔可夫链的模型就定了。
三、隐马尔科夫模型(HMM)
是统计模型,用来描述一个含有隐含未知参数的马尔可夫过程。其难点是从可观察的参数中确定该过程的隐含参数。
具体实例:
假设你有一个住得很远的朋友,他每天跟你打电话告诉你他那天做了什么。你的朋友仅仅对三种活动感兴趣:公园散步,购物以及清理房间。他选择做什么事情只凭天气。你对于他所住的地方的天气情况并不了解,但是你知道总的趋势。在他告诉你每天所做的事情基础上,你想要猜测他所在地的天气情况。
你认为天气的运行就像一个马尔可夫链,它有两个状态 “雨"和"晴”,但是你无法直接观察它们,也就是说,它们对于你是隐藏的。每天,你的朋友有一定的概率进行下列活动:“散步”、“购物”、“清理”。因为你朋友告诉你他的活动,所以这些活动就是你的观察数据。这整个系统就是一个隐马尔可夫模型HMM。
四、马尔可夫决策过程(MDP)
在每个时间步,该过程处于某种状态 s s s ,决策者可以选择任何一个在状态 s s s可得到的行动 a a a。该过程通过随机移动到下一个状态 s ′ s' s′来响应下一个时间步骤,并给决策者一个相应的奖励 R a ( s , s ′ ) R_a(s,s') Ra(s,s′)
MDP: ( S , A , P a , R a ) (S, A, P_a, R_a) (S,A,Pa,Ra)
- s s s是一组有限的状态
- A A A是一组有限的动作
- P a P_a Pa是行动 a a a 的概率
- R a R_a Ra行动 a a a 的奖励
MDP是马尔可夫链的延伸,不同之处在于增加了行动(允许选择)和奖励(给予动力)。可以使用MDP来搜索最大化随机奖励的策略,即选择最优策略。
五、部分可观察马尔可夫决策过程(POMDP)
POMDP,部分可观马尔可夫决策过程,特点是 A g e n t Agent Agent的当前状态不完全可观,即不能直接检测到。定义信念状态空间,描述当前所处可能状态的概率分布,记为 b b b。离散时间的POMDP可以用以下七元组来表示 ( S , A , T , R , Ω , O , γ ) (S,A,T,R,Ω,O,γ) (S,A,T,R,Ω,O,γ),其中:
- S S S 代表一组有限的离散状态;
- A A A 代表一组离散的行动;
- T T T 是状态转移函数,表示状态之间的一组转移概率, T ( s , a , s ′ ) : = P r ( s t + 1 = s ′ ∣ s t = s , a t = a ) T(s,a,s'):=Pr(s_{t+1}=s'|s_{t}=s,a_{t}=a) T(s,a,s′):=Pr(st+1=s′∣st=s,at=a)表示在状态 s s s执行动作 a a a达到状态 s ′ s' s′ 的概率。
- Ω Ω Ω 是一组观察,用以提供关于不确定环境的信息。
- O O O 表示一组条件观察概率, O ( s ′ , a , o ′ ) : = P r ( o t + 1 = o ′ │ a t = a , s t + 1 = s ′ ) O(s',a,o' ):=Pr(o_{t+1}=o'│a_{t}=a,s_{t+1}=s' ) O(s′,a,o′):=Pr(ot+1=o′│at=a,st+1=s′) 表示执行动作 a a a达到状态 s ′ s' s′观察到 o ′ o' o′ 的概率。
- 回报函数 R ( s , a ) R(s,a) R(s,a) 表示在 s s s上执行行动 a a a所得到的即时回报。
- γ ∈ [ 0 , 1 ] γ∈[0,1] γ∈[0,1]是折扣因子。
简单的POMDP问题求解思路:
- 建立POMDP模型:确定 S t a t e State State、 A c t i o n Action Action、 O b s e r v a t i o n Observation Observation;状态转移函数、观察函数、回报函数、折扣
- 给定初始信念状态
- 选择合适的第一步 a c t i o n action action,迭代更新信念状态

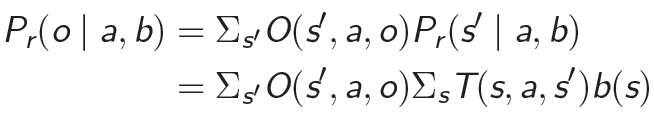
- 根据信念状态迭代更新的过程中得到的 a c t i o n action action序列,求出总的折扣回报。这里的序列长度(即迭代的步数)可以是指定的最大步数、或者在任何被终止的步骤停止。
POMDP求解面临的两大问题
POMDP规划问题的难解源于“维数诅咒”和“历史诅咒”。
- 维数诅咒:
- 历史诅咒:随着规划步数的增加,整个搜索树所包含的历史数越来越多,呈指数级别的增长。
POMDP近似规划算法:离线算法、在线算法
根据规划方式的不同,POMDP近似规划算法可分成两类,即离线规划算法和在线规划算法。
- 离线规划算法:由策略搜索和策略执行两个阶段组成,先在策略搜索阶段用大量的预处理时间产生整个信念状态空间上的策略,然后用这个策略在策略执行阶段进行决策。由于离线规划算法的预处理时间可以被平均分摊到每次的任务中,因而它们适合求解重复的POMDP规划任务。
- 在线规划算法:适合处理紧急的或一次性的POMDP规划任务。不会分配大量时间给预处理过程,而是在基于当前状态且时间有限的策略搜索步和策略执行步间迭代。在策略搜索步,在线规划算法重点在于计算好当前信念状态处的局部策略,而不是可以泛化到整个信念状态空间的全局策略。
因而,较离线规划算法而言,在线规划算法有潜力在保证产生高回报的行动系列的同时,用于策略搜索步和策略执行步的总时间小得多。因此,在线规划算法被认为是求解大规模POMDP问题的一类有研究前景的近似规划算法。
Value Iteration
POMDP规划的目标是找到一系列行动{ a 0 , . . . , a t a_0,...,a_t a0,...,at}来最大化期望回报 E [ ∑ t γ t R ( s t , a t ) ] E[\sum_t{\gamma^t R(s_t,a_t)}] E[∑tγtR(st,at)]。由于在POMDP中每个状态不能被完全观测到,我们需要为每个belief最大化期望回报。因此,值函数为:
V ( b ) = m a x a ∈ A [ R ( b , a ) + γ ∑ b ′ ∈ B T ( b , a , b ′ ) V ( b ′ ) ] V(b)=max_{a \in A}[R(b,a)+\gamma\sum_{b^{'} \in B}T(b,a,b^{'})V(b^{'})] V(b)=maxa∈A[R(b,a)+γb′∈B∑T(b,a,b′)V(b′)]
在迭代n次之后,我们要的值函数就可以表示为一系列 α − v e c t o r \alpha-vector α−vector了: V n = { α 0 , α 1 , . . . , α m } V_n=\{\alpha_0,\alpha_1,...,\alpha_m\} Vn={α0,α1,...,αm},每个 α − v e c t o r \alpha-vector α−vector定义了belief simplex上某个区域里的值函数:
V n ( b ) = m a x α ∈ V n ∑ s ∈ S α ( s ) b ( s ) V_n(b)=max_{\alpha \in V_n}{\sum_{s\in S}{\alpha(s)b(s)}} Vn(b)=maxα∈Vns∈S∑α(s)b(s)
α-向量
-
定义: α a = R ( ⋅ , a ) α_a=R(·,a) αa=R(⋅,a)
-
理解:在转移矩阵、观察矩阵、回报函数确定的情况下,行动空间 A c t i o n Action Action中的每一个动作 a a a对应一个α-向量,它的组成元素为“在状态空间中每一个状态下采取特定动作 a a a所获得的回报”。
-
作用:用于确定最优的行动序列。以2维问题为例(只有两个状态),每一个α-向量[x1,x2]都可视为一条直线,有几个动作就有几条直线,将所有的直线绘制在同一副图中(横坐标为状态 s s s、纵坐标为回报值),如下图所示,这些直线会形成一个分段线性凸函数(红色部分所示),这部分就显示了当状态落在哪个区域里采取哪个行动能使回报最大。

-
求解:
(1)一步策略问题:直接求 R ( ⋅ , a ) R(·,a) R(⋅,a)
(2)多步策略问题:固定动作 a a a进行值迭代
注:一般不需要自己求解,掌握求解的过程有助于理解POMDP问题求解的过程。 -
POMDP求解可能面临的问题:Curse of Dimensionality和Curse of History,也就是当state的维数或者planning过程中horizon数量增加的时候,运算成本将几何级增长。
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!