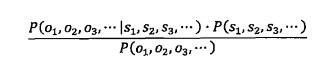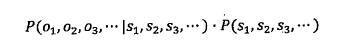隐含马尔可夫模型

语言和通信之间存在天然的联系。两个人对话的时候说话的一方就相当于是信息源，而声带、空气等就相当于是传输的通道，听的一方相当于信息的接收方。

那么现在要做的就是根据接收端的观测信号o1, o2, o3...推测信号源发送的信息s1,s2,s3...。其实这就需要从所有的源信息中找到最可能产生出观测信号的哪一个信息即

P(s1,s2,s3...|o1,o2,o3...)需达到最大值。根据贝叶斯公式，上述公式可转换为

这个公式看似复杂，但是一旦信息形成，其实P(o1,o2,o3...)是固定的。因此上述公式可简化为

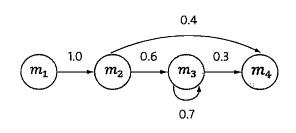
接下来就是介绍隐含马尔可夫模型。在这之前先介绍马尔科夫链。随着概率论从对随机变量的研究发展到对随机过程的研究，这其中的研究方法变得复杂了许多。什么是随机过程，即任意一时刻t，对应的状态s(t)都是随机的，且st的取值可能与周围其他的状态相关。这样问题就变得十分复杂。为了简化问题，马尔可夫提出了一种假设，即随机过程中各个状态st的概率分布，只与他的前一个状态s(t-1)有关即P(s(t)|s1,s2,s3...s(t-1))=p(s(t)|s(t-1))。这个假设就被称为马尔可夫假设，符合这个假设的随机过程则被成为马尔可夫链或马尔可夫过程。下图描述的为一个马尔可夫链

四个圈表示四个状态，每条边表示一个转换过程，边上的权值代表转换概率。例如，P(s(t+1

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！