最后的晚餐(dinner)

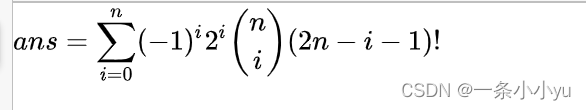
题目描述

    **YZ（已被和谐）的食堂实在是太挤辣！所以Apojacsleam现在想邀请他的一些好友去校外吃一顿饭，并在某酒店包下了一桌饭。

    当Apojacsleam和他的同学们来到酒店之后，他才发现了这些同学们其实是N对cp，由于要保护广大单身狗的弱小心灵（FF！），所以他不想让任意一对情侣相邻。

    说明：

        ·酒店的桌子是恰好有2N个位置的圆桌。

        ·客人恰好是N对cp，也就是说，圆桌上没有空位。

        ·桌子的每一个位置是一样的，也就是说，如果两种方案可以通过旋转得到，那么这就可以视为相等的。

    现在，你需要求出，将任意一对情侣不相邻的方案数。

方法1：

首先这是一个环，所以1234与2341是同样的方案，那么从n对情侣中先把男生挑出来共n个人先去坐位子，共(n-1)!个方案。

接下来就是把剩下n个人插入进去了。
定义dp[i]代表安排完前i个人的时候的方案数。

1、dp[i-1] * (n+i-3)

上面的式子是直接插入方式，安排第i个人的时候，一共有n+i-1个人，那么就有n-i+1个位置可以选，但是又不能和自己情侣相邻，减掉她左右的两个位置即可。

2、dp[i-2] * (i-1) * 2

这个式子是间接插入，就是说现在在安排第i个人，但是第i-1个人我暂时安排他和他情侣在一起，把第i个人插入他们两者之间即可最后正常。

所以通过观察间接插入和直接插入是完全独立的两个方案，不会出现重复，注意特判一下n=1的情况即可。
所以最终答案就是 dp[i] = dp[i-1] * (n+i-3) + dp[i-2] * (i-1) * 2
最终把分配男生的(n-1)!的方案乘进去即可。

#include 
#include 
using namespace std;
const int N=30000000;
const long long mod=1000000007;
long long f[N+5];
int main(){int n;scanf("%d",&n);if(n==1){printf("0");return 0;}f[0]=1;f[1]=n-2;for(int i=2;i<=n;i++)f[i]=(f[i-1]*(n+i-3)%mod+f[i-2]*(i-1)%mod*2%mod)%mod;for(int i=2;i

#include
using namespace std;
typedef long long LL;
const LL N=3e7+5,mod=1000000007,INV=500000004;
LL fac,tfac,inv[N],po=1;
LL ksm(LL a,LL n)
{LL res=1;while(n){if(n&1)res=res*a%mod;a=a*a%mod;n>>=1;}return res;
}
void init(LL n)
{tfac=1;for(LL i=1;i<=n;i++)tfac=tfac*i%mod,po=po*2%mod;fac=tfac*ksm(n,mod-2)%mod;inv[n]=ksm(tfac,mod-2);for(LL i=n-1;~i;i--)inv[i]=inv[i+1]*(i+1)%mod;//inv[1]=inv[0]=1;
}
LL C(LL a,LL b)
{//if(a

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！