文章目录

• 高维数据降维-拉普拉斯特征映射
• 拉普拉斯矩阵
• • 1.1无向权重图
  • 1.2拉普拉斯矩阵
  • 1.3LE算法
• 拉普拉斯特征映射基本步骤：
• • 例子

高维数据降维-拉普拉斯特征映射

高维数据降维是指采用某种映射方法，降低随机变量的数量，例如将数据点从高维空间映射到低维空间中，从而实现维度减少。

降维的过程是通过对输入的原始数据特征进行学习，得到一个映射函数，实现将输入样本映射后到低维空间中之后，原始数据特征并没有明显的损失，通常情况下新空间的维度要小于原空间的维度。目前大部分降维算法是处理向量形式的数据。

拉普拉斯矩阵

1.1无向权重图

我们一般使用$G(V,E)$表示一个图，其中 $V$ 表示图中的顶点 { v 1 , v 2 , . . . , v n } \{v_1,v_2,...,v_n\} {v1​,v2​,...,vn​} , $E$表示顶点和顶点之间的边。定义 w i j w_{ij} wij​ 为顶点 v i v_i vi​ 和 v j v_j vj​ 之间的权重。对于一个有 $n$个节点的图，可以得到一个大小为 $(n,n)$ 的权重矩阵 $W$ 。根据图中度的定义，我们可以得到图的度矩阵 $D$ ，$D$ 是一个对角矩阵，其中 d i i d_{ii} dii​ 表示顶点 v i v_i vi​ 的度。其中：

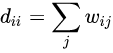
1.2拉普拉斯矩阵

拉普拉斯矩阵为$L=D-W$,具有如下性质

对任意向量$f$有：

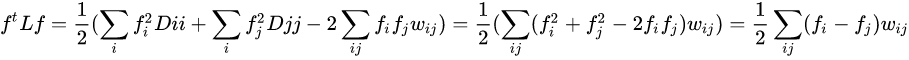
1.3LE算法

LE算法是一种保留数据局部特征的流形降维算法。其主要思想是在低维空间内尽可能保留数据局部样本点之间的结构不变。
假设原始数据集为 X = x i , x 2 , . . . , x n X=x_i,x_2,...,x_n X=xi​,x2​,...,xn​,为一个（n,m）的数据集。

1. 高维空间样本结构描述
在高维空间使用构建K-近邻图的方法来描述局部样本点之间的结构。对于样本点 x i x_i xi​,如果样本点 x j x_j xj​于其互为近邻，则有：

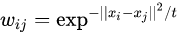
其中$t$ 是一个自己指定的常数。如果 x j x_j xj​ 不是其近邻，则

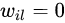
最后得到的 $W$矩阵就是高维空间样本点的结构矩阵。由于这个结构矩阵只存放每个点和其K近邻点的结构关系，(不是K近邻的点，权重值通通为0)，所以LE算法只能保留数据的局部结构。

2. 低维空间样本保留结构
我们设降维之后的矩阵为 Y = y 1 , y 2 , . . , y n Y=y_1,y_2,..,y_n Y=y1​,y2​,..,yn​,是一个（n,k）的数据集，为了在低维空间中也保留高维的结构性，定义如下目标函数：

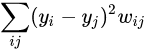
上述函数的表示如果在高维空间中两点距离越近，则在低维空间中两点的距离也越近，这样可以在低维空间尽可能的保留高维空间样本点的结构。根据拉普拉斯矩阵的性质可得：

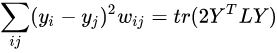
为了消除低维空间中的缩放因子，也为了保证 D i i D_{ii} Dii​值较大的样本点在低维空间中更为重要，添加如下限制：

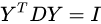
最终的LE算法的优化目标：


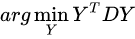
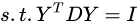
此时就将优化目标函数问题转换成为了广义特征值分解问题：

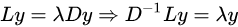
拉普拉斯特征映射基本步骤：

(1) 构建无向图，将所有的样本以点连接成一个图，例如使用 KNN 算法，将每个点最近的 k 个点进行连接，其中 k 是自己设定的值；

(2) 构建图的权值矩阵，通过点之间的关联程度来确定点与点之间的权重大小，例如，两个点之间如果相连接，则权重为1，否则为0；

(3) 特征映射，通过公式 L y = λ D y L_{y} = \lambda D_{y} Ly​=λDy​ 计算拉普拉斯矩阵 L 的特征向量和特征值，用最小的 m 个非零特征值对应的特征向量作为降维的结果。

例子

# 例子：
from sklearn import manifold, datasets
import numpy as np
import matplotlib.pyplot as pltX,color = datasets.make_swiss_roll(n_samples = 1500)ax = plt.subplot(projection = '3d')
# 原始数据
ax.scatter(X[:,0],X[:,1],X[:,2],c = color, cmap=plt.cm.Spectral)  
# 调整三维视角
ax.view_init(4,-50)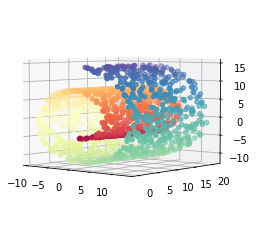  

# 2维10个近邻点
se = manifold.SpectralEmbedding(n_components=2,n_neighbors=10)
# 将原始样本投射到新的子空间中
Y = se.fit_transform(X)  # LE 降维后可视化
plt.scatter(Y[:,0],Y[:,1],c=color,cmap=plt.cm.Spectral)

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！