洛谷P1508(动态规划)如何才能吃的最多解析

题目描述

正处在某一特定时期之中的李大水牛由于消化系统比较发达，最近一直处在饥饿的状态中。某曰.上课，正当他饿得头昏眼花之时，眼前突然闪现出了一个n* m(n and m < = 200)的矩型的巨型大餐桌，而自己正处在这个大餐桌的一-侧的中点下边。餐桌被划分为了n*m个小方格，每一个方格中都有一个圆形的巨型大餐盘，上面盛满了令李大水牛朝思暮想的食物。李大水牛已将餐桌上所有的食物按其所能提供的能量打了分(有些是负的，因为吃了要拉肚子)，他决定从自己所处的位置吃到餐桌的另一侧，但他吃东西有一个习惯一只吃自 己前方或左前方或右前方的盘中的食物。
由于李大水牛已饿得不想动脑了，而他又想获得最大的能量，因此，他将这个问题交给了你。
每组数据的出发点都是最后一行的中间位置的下方!
输入
第一行为m n.(n为奇数)，李大水牛- -开始在最后一行的中间的下方接下来为m* n的数字距阵.
共有m行，每行n个数字数字间用空格隔开.代表该格子上的盘中的食物所能提供的能量.数字全是整数.

输出
一个数,为你所找出的最大能量值

题目分析

此题给出了mXn矩阵, 矩阵元素的值有正有负, 由于只能向前前进, 不能水平向左/右前行,
所以此题抽象出来就是从最下层出发, 每一层只能从正上方/左上方/右上方取一个元素, 使得所取元素和最大

下面说到矩阵的长度, 我使用length来代替, 宽度用width

假如我们用一个dp数组来存储吃掉某个元素后能获得的最大能量
故我们开一个大小为width的dp数组
dp[i]表示吃i后, 能获得的最大总能量值
下面我用 [s,e]表示起始点的x的范围为s, s+1, s+2…e-1, e

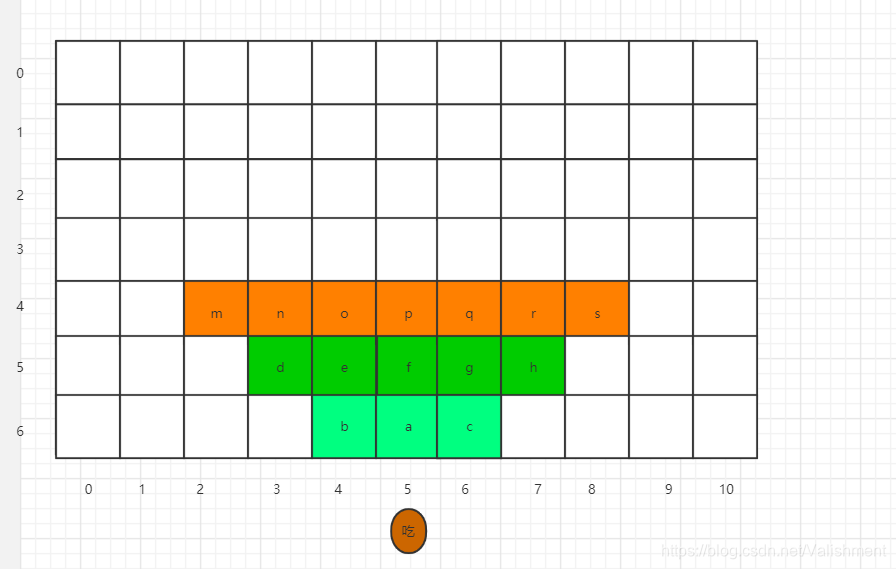
举例

假设m = 11, n = 7
第一次吃, 必须从中点出发, (0 + 10) / 2 = 5. 所以从5开始出发
那么第一次吃可能的选择如图浅绿色表示(起始点-----[5, 5])

因为上一次吃, 可以吃到b, a, c中的一个, 而他们的x坐标的范围是[4, 6], 所以第二次吃可能的选择如图深绿色表示(起始点-----[4, 6]),

同理可得第三次吃可能的选择如图橘色表示(起始点-----[3, 7])

.
.
.
随着我们一次次往后面吃, 可供选择的范围越来越大了, 而我只想要有最优解, 也就是元素和最大的那一个, 该怎么办呢? 一般来说, 用动态规划解题, 我么想要求得什么结果, 在dp里最好就存储什么.

分析

i 表示上一次所在的层数, j 表示列数

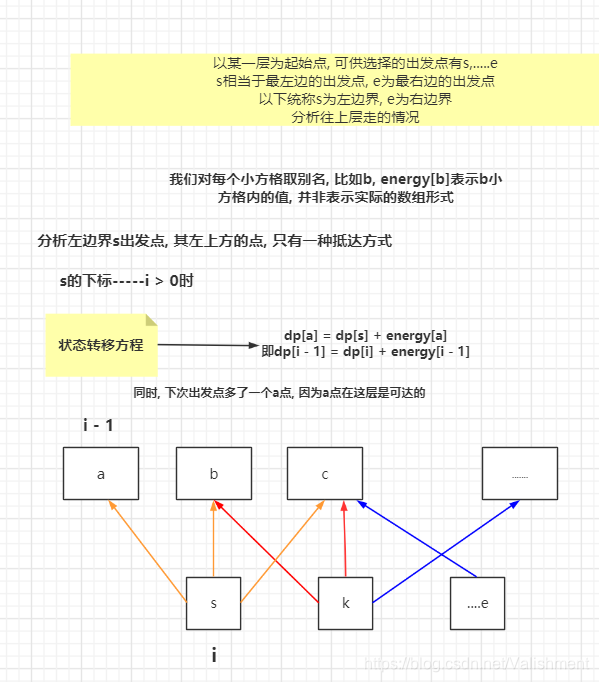
1.对可供选择的出发点的边界进行分析, 如左边界

1. 向左前方行进(当j > 0 时, 才可以向左前方吃)
   如果从左边界向左前方行进, (第一次b, 第二次d, 第三次m)
   其转移方程为 dp[i][j - 1] = dp[i - 1][j] + energy[i][j - 1] (j > 0 && j == s )

此方程对右边界也成立

再拿上图分析

dp[5][3] = dp[6][4] + energy[5][3];
dp[4][2] = dp[5][3] + energy[4][2];
…

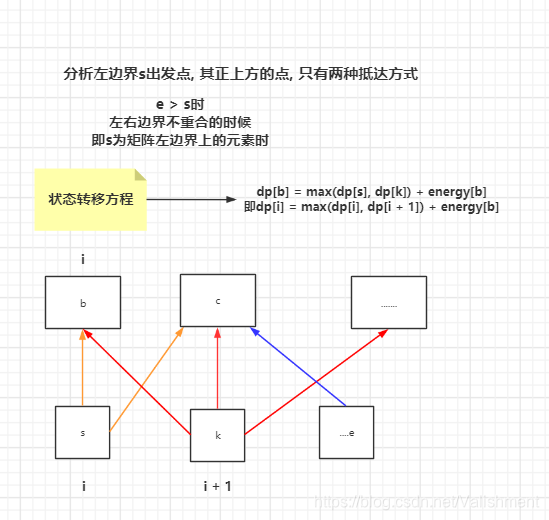
2. 向正前方行进
   还是拿左边界举例
   第一次a, 第二次(e,g), 第三次(n,r)…
   (左边界)状态转移方程为:
   dp[i][j] = max(dp[i][j], dp[i][j + 1]) + energy[i][j]------(s < e)
   dp[i][j] = max(dp[i][j]) + energy[i][j]---------------------(s == e)
   (右边界)状态转移方程为:
   dp[i][j] = max(dp[i][j - 1], dp[i][j]) + energy[i][j]------(s < e)
   dp[i][j] = max(dp[i][j]) + energy[i][j]---------------------(s == e)
   再次进行分析

得到:
dp[4][3] = max(dp[5][3], dp[5][4]) + energy[4][3];
dp[4][7] = max(dp[5][7], dp[5][6]) + energy[4][7];

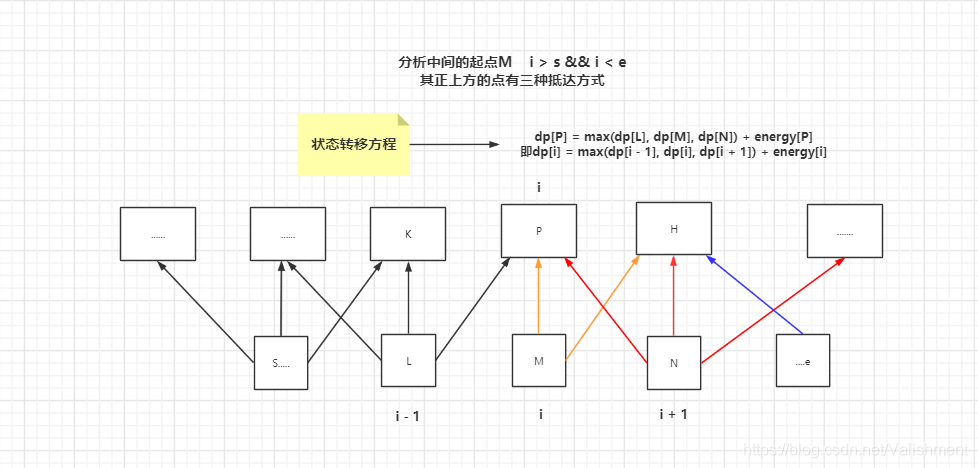
对非边界进行分析

1. 对[s + 1, e - 1]列内的元素进行规划
   状态转移方程: dp[i][j] = max(dp[i + 1][j - 1], dp[i + 1][j ], dp[i + 1][j + 1];

如此, 解决了每一层的dp, 我们要得到答案, 只需要分析dp[0][0,1,2,3…width - 1], 这些元素值表示: 最后吃energy[0][j] 时, 获取到的最大总能量
我们对这些值进行升序排序, 然后取最大即可.

状态转移方程归纳

1. dp[i][j - 1] = dp[i - 1][j] + energy[i][j - 1] (j > 0)(j == s || j == e)
2. dp[i][j] = max(dp[i][j], dp[i][j + 1]) + energy[i][j]------(s < e && j == s)
   dp[i][j] = max(dp[i][j]) + energy[i][j]---------------------(s == e && j == s)
   dp[i][j] = max(dp[i][j], dp[i][j - 1]) + energy[i][j]------(s < e && j == e)
   dp[i][j] = max(dp[i][j]) + energy[i][j]---------------------(s == e && j == e)
3. dp[i][j] = max(dp[i + 1][j - 1], dp[i + 1][j ], dp[i + 1][j + 1]; (j > s && s < e)

另一种解释

C++代码:

11/13更正代码中sort()部分出现的边界错误

#include
#include
using namespace std;int main(){int length, width;cin >> length >> width;int ** energy = new int*[length];for (int i = 0; i < length; ++i) {energy[i] = new int[width];}for (int i = 0; i < length; ++i) {for (int j = 0; j < width; ++j) {cin >> energy[i][j];}}int start, end;end = start = width / 2;int layer;int * dp = new int[width]{0};for (int i = 0; i < length; ++i) {int * newdp = new int[width]{0};layer = length - 1 - i;if(start == end){newdp[start] = dp[start] + energy[layer][start];} else{newdp[start] = max(dp[start], dp[start + 1]) + energy[layer][start];newdp[end] = max(dp[end], dp[end - 1]) + energy[layer][end];}for (int j = start + 1; j <= end - 1; ++j) {newdp[j] = max(max(dp[j - 1], dp[j]), dp[j + 1]) + energy[layer][j];}if(start > 0){newdp[start - 1] = dp[start] + energy[layer][start - 1];--start;}if(end < width - 1){newdp[end + 1] = dp[end] + energy[layer][end + 1];++end;}dp = newdp;}sort(dp, dp + width);cout << dp[width - 1] << endl;return 0;
}

总结:

此题中, 一个点的状态可能与1个/2个/3个有关, 这取决于它的位置, 针对边界, 会出现两种情况, 它可能直接决定了其左前方点的状态, 也可能与其右边一个点共同决定其前方点的状态, 我们对每种可能出现的状态中, 取最大值.
而对于中间的点, 它与左边&右边一个点, 三个点, 共同决定其前方点的状态.

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！