网络流---EK模版

EK算法就是不断的从源点到汇点找增光路进行增广

有n个点，有m条有向边，有一个点很特殊，只出不进，叫做源点，通常规定为1号点。另一个点也很特殊，只进不出，叫做汇点，通常规定为n号点。每条有向边上有两个量，容量和流量，从i到j的容量通常用c[I,j]表示,流量则通常是f[I,j]。通常可以把这些边想象成道路，流量就是这条道路的车流量，容量就是道路可承受的最大的车流量。很显然的，流量<=容量。而对于每个不是源点和汇点的点来说，可以类比的想象成没有存储功能的货物的中转站，所有”进入”他们的流量和等于所有从他本身”出去”的流量。
把源点比作工厂的话，问题就是求从工厂最大可以发出多少货物，是不至于超过道路的容量限制，也就是，最大流。

下面我们来考虑如何求最大流。
首先，假如所有边上的流量都没有超过容量(不大于容量)，那么就把这一组流量，或者说，这个流，称为一个可行流。一个最简单的例子就是，零流，即所有的流量都是0的流。
我们就从这个零流开始考虑，假如有这么一条路，这条路从源点开始一直一段一段的连到了汇点，并且，这条路上的每一段都满足流量<容量，注意，是严格的<,而不是<=。那么，我们一定能找到这条路上的每一段的(容量-流量)的值当中的最小值delta。我们把这条路上每一段的流量都加上这个delta，一定可以保证这个流依然是可行流，这是显然的。
这样我们就得到了一个更大的流，他的流量是之前的流量+delta，而这条路就叫做增广路。
我们不断地从起点开始寻找增广路，每次都对其进行增广，直到源点和汇点不连通，也就是找不到增广路为止。当找不到增广路的时候，当前的流量就是最大流，这个结论非常重要。
寻找增广路的时候我们可以简单的从源点开始做bfs，并不断修改这条路上的delta量，直到找到源点或者找不到增广路。

但事实上并没有这么简单，上面所说的增广路还不完整，比如说下面这个网络流模型

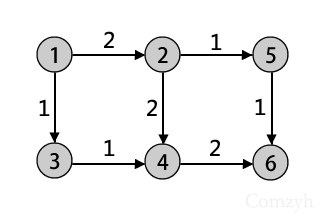
在这幅图中我们首先要增广1->2->4->6,这时可以获得一个容量为2的流,但是如果不建立4->2反向弧的话,则无法进一步增广,最终答案为2,显然是不对的,然而如果建立了反向弧4->2,则第二次能进行1->3->4->2->5->6的增广,最大流为3.

Comzyh对反向弧的理解可以说是”偷梁换柱“,请仔细阅读:在上面的例子中,我们可以看出,最终结果是1->2->5->6和1->2->4->6和1->3->4->6.当增广完1->2->4->5(代号A)后,在增广1->3->4->2->5->6(代号B),相当于将经过节点2的A流从中截流1(总共是2)走2->5>6,而不走2->4>6了,同时B流也从节点4截流出1(总共是1)走4->6而不是4->2->5->6,相当于AB流做加法.

简单的说反向弧为今后提供反悔的机会,让前面不走这条路而走别的路.

以上摘自https://comzyh.com/blog/archives/568/
http://blog.csdn.net/pi9nc/article/details/23339111

第一种：书上的模版

#include 
#include 
#include 
#include 
#include 
using namespace std;
#define N 1010
#define INF 0x3f3f3f3fstruct Edge{int from, to, cap, flow;Edge() {}Edge(int from, int to, int cap, int flow): from(from), to(to), cap(cap), flow(flow){}
};struct EK{vector<int> G[N];vector edges;int s, t, n, m, p[N];bool vis[N];void init(int n, int m) {this->n = n; this->m = m;for (int i = 0; i <= n; i++)G[i].clear();edges.clear();}void AddEdge(int from, int to, int cap) {edges.push_back(Edge(from, to, cap, 0));edges.push_back(Edge(to, from, 0, 0));int m = edges.size();G[from].push_back(m - 2);G[to].push_back(m - 1);}bool BFS() {queue<int> q;memset(vis, 0, sizeof(vis));vis[s] = 1;q.push(s);while (!q.empty()) {int u = q.front();q.pop();for (int i = 0; i < G[u].size(); i++) {Edge &e = edges[G[u][i]];if (!vis[e.to] && e.cap > e.flow) {vis[e.to] = true;p[e.to] = G[u][i];if (e.to == t)return true;q.push(e.to);}}}return false;}int Augment() {int flow = INF, u = t;while (u != s) {Edge &e = edges[p[u]];flow = min(flow, e.cap - e.flow);u = e.from;}u = t;while (u != s) {edges[p[u]].flow += flow;edges[p[u] ^ 1].flow -= flow;u = edges[p[u]].from;}return flow;}int Maxflow(int s, int t) {this->s = s; this->t = t;int flow = 0;while (BFS()) {flow += Augment();}return flow;}
};EK ek;int main() {return 0;
}

第二种：改进的模版

#include 
#include 
#include 
#include 
#include 
using namespace std;
const int MAXNODE = 210;
const int MAXEDGE = 100010;
typedef int Type;
const Type INF = 0x3f3f3f3f;struct Edge{int u, v, next;Type cap, flow;Edge() {}Edge(int u, int v, Type cap, Type flow, int next): u(u), v(v), cap(cap), flow(flow), next(next){}
};struct EK{int n, m, s, t;Edge edges[MAXEDGE];int head[MAXNODE], pre[MAXNODE];bool vis[MAXNODE];vector<int> cut;void init(int n) {this->n = n;memset(head, -1, sizeof(head));m = 0;}void AddEdge(int u, int v, Type cap) {edges[m] = Edge(u, v, cap, 0, head[u]);head[u] = m++;edges[m] = Edge(v, u, 0, 0, head[v]);head[v] = m++;}//通过BFS构建层次图，并在层次图中找到增广路bool BFS() {queue<int> Q;memset(vis, 0, sizeof(vis));vis[s] = 1;Q.push(s);while (!Q.empty()) {int u = Q.front(); Q.pop();for (int i = head[u]; ~i; i = edges[i].next) {Edge &e = edges[i];if (!vis[e.v] && e.cap > e.flow) {vis[e.v] = true;pre[e.v] = i;if (e.v == t)return true;Q.push(e.v);}}}return false;}//增广，并修改每条边的流量Type Augment() {int u = t;Type flow = INF;while (u != s) {Edge &e = edges[pre[u]];flow = min(flow, e.cap - e.flow);u = e.u;}u = t;while (u != s) {edges[pre[u]].flow += flow;edges[pre[u] ^ 1].flow -= flow;u = edges[pre[u]].u;}return flow;}Type Maxflow(int s, int t) {this->s = s; this->t = t;Type flow = 0;while (BFS()) flow += Augment();return flow;}void Mincut() {cut.clear();for (int i = 0; i < m; i += 2) if (vis[edges[i].u] && !vis[edges[i].v] && edges[i].cap) cut.push_back(i);}
}ek;int main() {return 0;
}

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！